赶水镇中2011级初三(下)入学数学试题及答案
文档属性
| 名称 | 赶水镇中2011级初三(下)入学数学试题及答案 |

|
|
| 格式 | rar | ||
| 文件大小 | 138.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 新人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-02-17 00:00:00 | ||
图片预览




文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
赶水镇中2011级初三(下)入学检测 数学试题
(考试时间:120分钟 满分:150分 命题人:李开铜)
班级:__________姓名:_________
一、选择题(本大题10个小题,每小题4分,共40分)
1.的倒数是( )
A. 4 B. C. D.
2.如图,该几何体的俯视图是( )
A. B. C. D.
3. 计算的正确结果是( )
A. B. C. D.
4.如图,直线l截两平行直线a、b,则下列式子不一定成立的是( )
A.∠5=∠2 B. ∠2=∠4
C.∠3=∠5 D. ∠1=∠5
5.函数的自变量x的取值范围是( )
A. B. C. D.
6.已知⊙O1与⊙O2的半径分别为5cm和3cm,圆心距O1O2=2cm,则⊙O1与⊙O2的位置关系为( )
A. 外离 B. 外切 C. 内切 D. 相交
7.观察下列正方形的四个顶点所标的数字规律,那么2012这个数标在( )
A.第502个正方形的左下角 B.第502个正方形的右下角
C.第503个正方形的左下角 D.第503个正方形的右下角
8.某公司销售部有营销人员27人,销售部为了制定某种商品的销售定额,统计了这27人某月的销售量如下表:
每人销售量(单位:件) 600 500 400 350 300 200
人数(单位:人) 2 4 5 6 7 3
则该公司营销人员该月销售量的中位数是( ).
A. 500件 B. 400件 C. 350件 D. 300件
9.如图,图是长方形纸带,将纸带沿折叠成图再沿折叠成图则图中的的度数是( )
A.110° B.120° C.140° D.150°
10.如图,在等边△ABC中,M、N分别是边AB,AC的中点,
D为MN的中点,CD,BD的延长线分别交于AB,AC于
点E,点F,下列结论正确的是( )
①MN的长是BC的;②的面积是面积的;
③EM和FN的长度相等;④图中全等的三角形有4对;
⑤连接EF,则四边形EBCF一定是等腰梯形;
A. ①②⑤ B. ①③④ C. ①②④ D. ①③⑤
二、填空题:(本大题6个小题,每小题4分,共24分)
11.据2009年《重庆年鉴》记载,2009年全市财政收入1905000000元,用科学计数法表示为____________元。
12. 已知方程组{的解为{ ,则的值为 .
13.已知一个圆锥的底面圆半径为2cm,侧面展开图的半径长为5cm,则这个圆锥的侧面积是 。
14.在某时刻的阳光照耀下,高为4米的旗杆在水平地面上的影长为5米,附近一个建筑物的影长为20米,则该建筑物的高为_________.
15.某学校操场为长方形水泥地,面积约600平方米,长比宽多5米,若设该操场的长为米,则可得一元二次方程: .
16.如图所示,在矩形中,,两条对角线相交于点.以、为邻边作第1个平行四边形,对角线相交于点,再以、为邻边作第2个平行四边形,对角线相交于点;再以、为邻边作第3个平行四边形……依次类推.则
第10个平行四边形的周长是_______。
三、解答题(本大题4个小题,每小题6分,共24分)
17.计算:
18.解方程:.
19.解方程组:
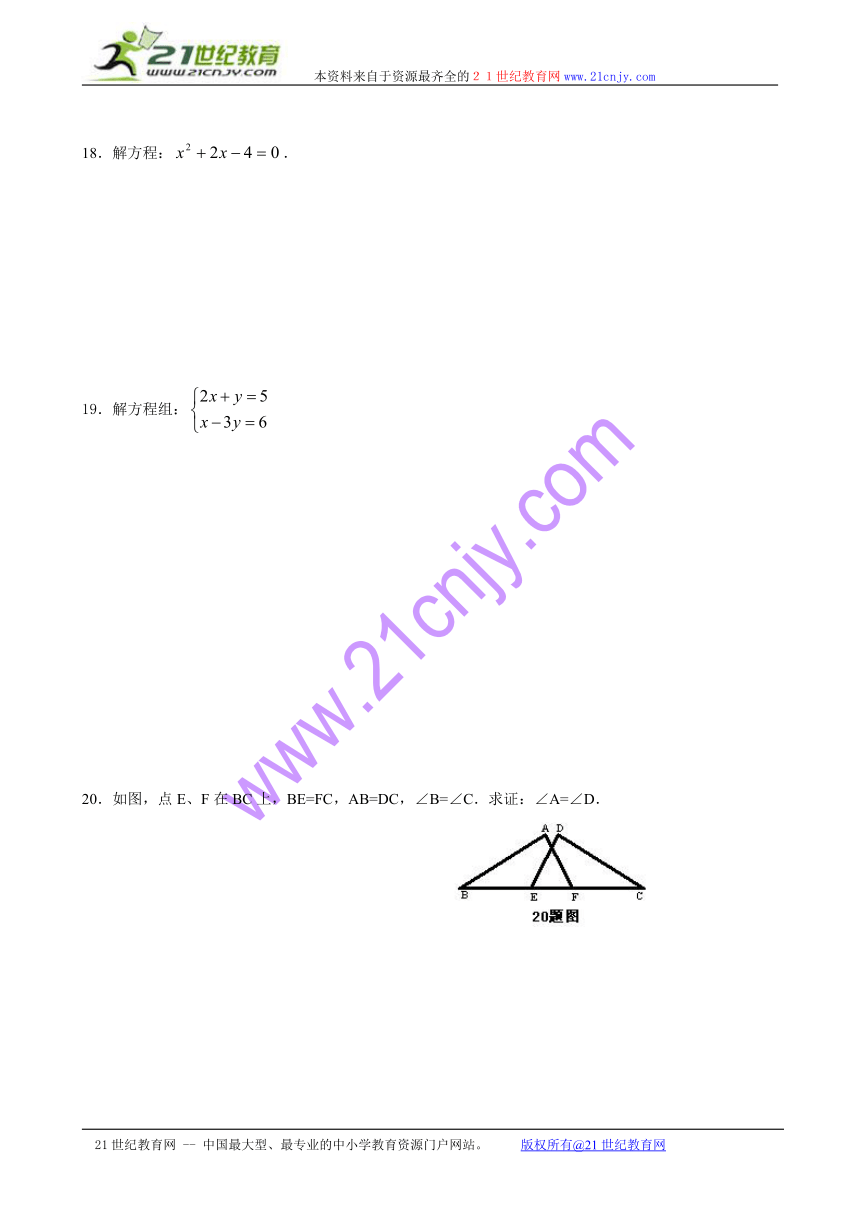
20.如图,点E、F在BC上,BE=FC,AB=DC,∠B=∠C.求证:∠A=∠D.
四、解答题(本大题4个小题,每小题10分,共40分)
21.如图,Rt△ABO的顶点A是反比例函数与一次函数的图象在第四象限的交点,AB⊥轴于B,且=.(1)求这个反比例函数和一次函数的解析式;
(2)求这个一次函数的图象与坐标轴围成的三角形的面积.
22.先化简,再求值:,其中.
23.如图是两个可以自由转动的转盘,甲转盘被等分成3个扇形,乙转盘被等分成4个扇形,每一个扇形上都标有相应的数字. 小亮和小华利用它们做游戏,游戏规则是:同时转动两个转盘,当转盘停止后,指针所指区域内的数字之和小于10,小华获胜;指针所指区域内的数字之和等于10,为平局;指针所指区域内的数字之和大于10,小亮获胜. 如果指针恰好指在分割线上,那么重转一次,直到指针指向一个数字为止.
(1)请你通过画树状图或者列表的方法分别求出小华和小亮获胜的概率.
(2)小华和小亮想用这两个转盘做游戏,他们规定:小华获胜时,小华得2分;小亮获胜时,小亮得3分. 这个游戏对双方公平吗?请说明理由;如果不公平,试修改得分规定,使游戏双方公平.
24.如图,在直角梯形中,为的中点,交 的延长线于
(1)证明:
(2)过作于连接试证明:
( http: / / )
五、解答题(本大题2个小题,其中25题10分,26题12分,共22分)
25.一快餐店试销某种套餐,试销一段时间后发现,每份套餐的成本为5元,该店每天固定支出费用为600元(不含套餐成本)。若每份售价不超过10元,每天可销售400份;若每份售价超过10元,每提高1元,每天的销售量就减少40份。为了便于结算,每份套餐的售价x(元)取整数,且要求售价一定高于成本价,用y(元)表示该店日销售利润.(日销售利润=每天的销售额-套餐成本-每天固定支出)
(1)当每份套餐售价不超过10元时,请写出y与x的函数关系式及自变量的取值范围;
(2)当每份售价超过10元时,该店既要吸引顾客,使每天销售量较大,又要有最高的日销售利润。按此要求,每份套餐的售价应定为多少元?此时日销售利润为多少?
(3)新年即将到来,该快餐店准备为某福利院30个小朋友送去新年的礼物,已知购买一份礼物需要20元,于是快餐店统一将套餐的售价定为10元以上,并且每卖出一份快餐就捐出2元作为为福利院小朋友购买礼物的经费,则快餐店在售价不超过14元的情况下至少将套餐定为多少钱一份,可使日销售利润(不包含已捐出的钱)达到900元?并通过分析判断此时所集经费是否能够为福利院每个小朋友都购买一份礼物。
(其中,)
26.如图所示, 在平面直角坐标系xoy中, Rt△AOB的直角边OB,OA分别在x轴上和y轴上,其中OA=2,OB=4,现将Rt△AOB绕着直角顶点O按逆时针方向旋转90°得到△COD,已知一抛物线经过C、D、B三点。
1)求这条抛物线的解析式;
(2)连接DB,P是线段BC上一动点(P不与B、C重合),过点P作PE∥BD交CD于E,则当△DEP面积最大时,求PE的解析式。
(3)作点D关于此抛物线对称轴的对称点F,连接CF交对称轴于点M,抛物线上一动点R,x轴上一动点Q, 则在抛物线上是否存在点R,x轴上是否存在点Q,使得以C、M、Q、R为顶点的四边形是平行四边形 如果存在, 求出Q点的坐标, 如果不存在, 请说明理由.
赶水镇中2011级初三(下)入学检测数学试题 参考答案
一.选择题:
序号 1 2 3 4 5 6 7 8 9 10
答案 D C A A C C C C B D
二.填空题:(本题共6个小题,每小题4分,共24分请将答案填写在下列方框中)
序号 11 12 13 14 15 16
答案 1.905×109 16m
三.解答题:(本题共4题,每小题6分,共24分)
17.计算:==1
18.,
19.,.
20. ∵BE=FC ∴BF=CE 又∵AB=CD ∠B=∠C
∴△ABF≌△DCE ∴ ∠A= ∠D
四、解答题(本大题4个小题,每小题10分,共40分)
21.(1) ∵S△ABO= ∴K=-5 ∴ (2)面积为:8.
22.解:原式= ∴将中.
则
23. (1)
6 7 8 9
1 (1,6) (1,7) (1,8) (1,9)
2 (2,6) (2,7) (2,8) (2,9)
3 (3,6) (3,7) (3,8) (3,9)
由表可知:共有12种等可能的结果,其中和小于10的有6种,和大于10的有3种
, ............ 2分
(2) ,
∴不公平
修改规则为:小华获胜时得1分,小亮获胜时得2分,其他规则不变 ........ 2分
24.(1) 证明
,
E为CD的中点
(2)连接GA ,
四边形ABGD是矩形,
由(1)得
由(1)得EF=EA
五、解答题(本大题2个小题,其中25题10分,26题12分,共22分)
25. 解(1)y=(x-5)·400-600
=400x-2600(5(2)当x>10时
y=(x-5) ·[400-(x-10).40]-600
= -40x2+1000x-4600
=-40(x2-25x+)2--4600
= ……4分
又∵x只能为整数
∴当x=12或13时, 日销售利润最大,但为了吸引顾客,提高销量
x=12 ……5分
此时的日利润为:-40x(12-12.5)2+1650=1640元 ……6分
(3)y=(x-5-2)(400-(x-10) ·40) -600
=(x -7)(800-40x) -600
=-40x2+1080x-6200
令:-40x2+1080x-6200=900
2x2-54x+355=0
b2-4ac=76
……8分
套餐售价至少定为12天/份,可达到日销售利润为900元.
此时销售的份数为:400-(12-10) ·40
=400-80
=320份 ……9分
∴为福利园所集资金:
320×2=640元
∵30×20=600<640
∴快餐店所集经费能为福利院每个小朋友都购买一份礼物. ……10分
26.(1)∵△COD≌△AOB
∴OC=OA, OD=OB
∴OC=2, OD=4
∴C(-2,0) D(0,4) B(4,0)
∴设此抛物线的解析式
y=ax2+bx+4()
将C(-2,O) B(4,0)代入
∴
∴抛物线的解析式为: ……4分
(2)∵S△DEP=S△DCP- S△ECP
=
=
设点P(m,0)
∵P在BC之间运动
∴CP=m+2
∵PE//BD
∴△CEP≌△CDB
∴
∴
∴
∴S△DCP=
= ……6分
∴当m=1时,S△DEP有最大值为3,此时P(1,0) ……7分
又∵D(0,4)
又设BD的解析式y=kx+4()
将B(4,0)代入
0=4k+4
k = -1
∴BD:y= -x+4
∵PE//BD
∴设PE:y= -x+
将P(1,0)代入
0=-1+ =1
∴PE的解析式为:y= -x+1 ……8分
(3)存在
∵D(0,4) F(2,4)
CF:y=x + 2
∴M(1,3)
若 以CM为边
在y=中令y=3
x1=1+ x2=1-
∴Q1 (-2+,0) Q2(-2- ,0) ……10分
令y= -3,
x1=1+ x2=1-
Q3 (4+,0) Q4(4- ,0) ……12分
若 以CM为对角线,Q5与 Q1重合
∴共有四个点Q.
_
5
_
4
_
3
_
2
_
1
l
4题图
a
b
B
C
M
N
E
F
D
10题图
A1
O1
A2
B2
B1
C1
B
C2
A
O
D
第16题图
C
A
O
B
C
D
x
y
A
O
B
C
D
x
y
A
O
B
C
D
x
y
备用图(1)
备用图(2)
A
O
B
C
D
x
y
A
O
B
C
D
x
y
备用图(1)
H
P
E
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
赶水镇中2011级初三(下)入学检测 数学试题
(考试时间:120分钟 满分:150分 命题人:李开铜)
班级:__________姓名:_________
一、选择题(本大题10个小题,每小题4分,共40分)
1.的倒数是( )
A. 4 B. C. D.
2.如图,该几何体的俯视图是( )
A. B. C. D.
3. 计算的正确结果是( )
A. B. C. D.
4.如图,直线l截两平行直线a、b,则下列式子不一定成立的是( )
A.∠5=∠2 B. ∠2=∠4
C.∠3=∠5 D. ∠1=∠5
5.函数的自变量x的取值范围是( )
A. B. C. D.
6.已知⊙O1与⊙O2的半径分别为5cm和3cm,圆心距O1O2=2cm,则⊙O1与⊙O2的位置关系为( )
A. 外离 B. 外切 C. 内切 D. 相交
7.观察下列正方形的四个顶点所标的数字规律,那么2012这个数标在( )
A.第502个正方形的左下角 B.第502个正方形的右下角
C.第503个正方形的左下角 D.第503个正方形的右下角
8.某公司销售部有营销人员27人,销售部为了制定某种商品的销售定额,统计了这27人某月的销售量如下表:
每人销售量(单位:件) 600 500 400 350 300 200
人数(单位:人) 2 4 5 6 7 3
则该公司营销人员该月销售量的中位数是( ).
A. 500件 B. 400件 C. 350件 D. 300件
9.如图,图是长方形纸带,将纸带沿折叠成图再沿折叠成图则图中的的度数是( )
A.110° B.120° C.140° D.150°
10.如图,在等边△ABC中,M、N分别是边AB,AC的中点,
D为MN的中点,CD,BD的延长线分别交于AB,AC于
点E,点F,下列结论正确的是( )
①MN的长是BC的;②的面积是面积的;
③EM和FN的长度相等;④图中全等的三角形有4对;
⑤连接EF,则四边形EBCF一定是等腰梯形;
A. ①②⑤ B. ①③④ C. ①②④ D. ①③⑤
二、填空题:(本大题6个小题,每小题4分,共24分)
11.据2009年《重庆年鉴》记载,2009年全市财政收入1905000000元,用科学计数法表示为____________元。
12. 已知方程组{的解为{ ,则的值为 .
13.已知一个圆锥的底面圆半径为2cm,侧面展开图的半径长为5cm,则这个圆锥的侧面积是 。
14.在某时刻的阳光照耀下,高为4米的旗杆在水平地面上的影长为5米,附近一个建筑物的影长为20米,则该建筑物的高为_________.
15.某学校操场为长方形水泥地,面积约600平方米,长比宽多5米,若设该操场的长为米,则可得一元二次方程: .
16.如图所示,在矩形中,,两条对角线相交于点.以、为邻边作第1个平行四边形,对角线相交于点,再以、为邻边作第2个平行四边形,对角线相交于点;再以、为邻边作第3个平行四边形……依次类推.则
第10个平行四边形的周长是_______。
三、解答题(本大题4个小题,每小题6分,共24分)
17.计算:
18.解方程:.
19.解方程组:
20.如图,点E、F在BC上,BE=FC,AB=DC,∠B=∠C.求证:∠A=∠D.
四、解答题(本大题4个小题,每小题10分,共40分)
21.如图,Rt△ABO的顶点A是反比例函数与一次函数的图象在第四象限的交点,AB⊥轴于B,且=.(1)求这个反比例函数和一次函数的解析式;
(2)求这个一次函数的图象与坐标轴围成的三角形的面积.
22.先化简,再求值:,其中.
23.如图是两个可以自由转动的转盘,甲转盘被等分成3个扇形,乙转盘被等分成4个扇形,每一个扇形上都标有相应的数字. 小亮和小华利用它们做游戏,游戏规则是:同时转动两个转盘,当转盘停止后,指针所指区域内的数字之和小于10,小华获胜;指针所指区域内的数字之和等于10,为平局;指针所指区域内的数字之和大于10,小亮获胜. 如果指针恰好指在分割线上,那么重转一次,直到指针指向一个数字为止.
(1)请你通过画树状图或者列表的方法分别求出小华和小亮获胜的概率.
(2)小华和小亮想用这两个转盘做游戏,他们规定:小华获胜时,小华得2分;小亮获胜时,小亮得3分. 这个游戏对双方公平吗?请说明理由;如果不公平,试修改得分规定,使游戏双方公平.
24.如图,在直角梯形中,为的中点,交 的延长线于
(1)证明:
(2)过作于连接试证明:
( http: / / )
五、解答题(本大题2个小题,其中25题10分,26题12分,共22分)
25.一快餐店试销某种套餐,试销一段时间后发现,每份套餐的成本为5元,该店每天固定支出费用为600元(不含套餐成本)。若每份售价不超过10元,每天可销售400份;若每份售价超过10元,每提高1元,每天的销售量就减少40份。为了便于结算,每份套餐的售价x(元)取整数,且要求售价一定高于成本价,用y(元)表示该店日销售利润.(日销售利润=每天的销售额-套餐成本-每天固定支出)
(1)当每份套餐售价不超过10元时,请写出y与x的函数关系式及自变量的取值范围;
(2)当每份售价超过10元时,该店既要吸引顾客,使每天销售量较大,又要有最高的日销售利润。按此要求,每份套餐的售价应定为多少元?此时日销售利润为多少?
(3)新年即将到来,该快餐店准备为某福利院30个小朋友送去新年的礼物,已知购买一份礼物需要20元,于是快餐店统一将套餐的售价定为10元以上,并且每卖出一份快餐就捐出2元作为为福利院小朋友购买礼物的经费,则快餐店在售价不超过14元的情况下至少将套餐定为多少钱一份,可使日销售利润(不包含已捐出的钱)达到900元?并通过分析判断此时所集经费是否能够为福利院每个小朋友都购买一份礼物。
(其中,)
26.如图所示, 在平面直角坐标系xoy中, Rt△AOB的直角边OB,OA分别在x轴上和y轴上,其中OA=2,OB=4,现将Rt△AOB绕着直角顶点O按逆时针方向旋转90°得到△COD,已知一抛物线经过C、D、B三点。
1)求这条抛物线的解析式;
(2)连接DB,P是线段BC上一动点(P不与B、C重合),过点P作PE∥BD交CD于E,则当△DEP面积最大时,求PE的解析式。
(3)作点D关于此抛物线对称轴的对称点F,连接CF交对称轴于点M,抛物线上一动点R,x轴上一动点Q, 则在抛物线上是否存在点R,x轴上是否存在点Q,使得以C、M、Q、R为顶点的四边形是平行四边形 如果存在, 求出Q点的坐标, 如果不存在, 请说明理由.
赶水镇中2011级初三(下)入学检测数学试题 参考答案
一.选择题:
序号 1 2 3 4 5 6 7 8 9 10
答案 D C A A C C C C B D
二.填空题:(本题共6个小题,每小题4分,共24分请将答案填写在下列方框中)
序号 11 12 13 14 15 16
答案 1.905×109 16m
三.解答题:(本题共4题,每小题6分,共24分)
17.计算:==1
18.,
19.,.
20. ∵BE=FC ∴BF=CE 又∵AB=CD ∠B=∠C
∴△ABF≌△DCE ∴ ∠A= ∠D
四、解答题(本大题4个小题,每小题10分,共40分)
21.(1) ∵S△ABO= ∴K=-5 ∴ (2)面积为:8.
22.解:原式= ∴将中.
则
23. (1)
6 7 8 9
1 (1,6) (1,7) (1,8) (1,9)
2 (2,6) (2,7) (2,8) (2,9)
3 (3,6) (3,7) (3,8) (3,9)
由表可知:共有12种等可能的结果,其中和小于10的有6种,和大于10的有3种
, ............ 2分
(2) ,
∴不公平
修改规则为:小华获胜时得1分,小亮获胜时得2分,其他规则不变 ........ 2分
24.(1) 证明
,
E为CD的中点
(2)连接GA ,
四边形ABGD是矩形,
由(1)得
由(1)得EF=EA
五、解答题(本大题2个小题,其中25题10分,26题12分,共22分)
25. 解(1)y=(x-5)·400-600
=400x-2600(5
y=(x-5) ·[400-(x-10).40]-600
= -40x2+1000x-4600
=-40(x2-25x+)2--4600
= ……4分
又∵x只能为整数
∴当x=12或13时, 日销售利润最大,但为了吸引顾客,提高销量
x=12 ……5分
此时的日利润为:-40x(12-12.5)2+1650=1640元 ……6分
(3)y=(x-5-2)(400-(x-10) ·40) -600
=(x -7)(800-40x) -600
=-40x2+1080x-6200
令:-40x2+1080x-6200=900
2x2-54x+355=0
b2-4ac=76
……8分
套餐售价至少定为12天/份,可达到日销售利润为900元.
此时销售的份数为:400-(12-10) ·40
=400-80
=320份 ……9分
∴为福利园所集资金:
320×2=640元
∵30×20=600<640
∴快餐店所集经费能为福利院每个小朋友都购买一份礼物. ……10分
26.(1)∵△COD≌△AOB
∴OC=OA, OD=OB
∴OC=2, OD=4
∴C(-2,0) D(0,4) B(4,0)
∴设此抛物线的解析式
y=ax2+bx+4()
将C(-2,O) B(4,0)代入
∴
∴抛物线的解析式为: ……4分
(2)∵S△DEP=S△DCP- S△ECP
=
=
设点P(m,0)
∵P在BC之间运动
∴CP=m+2
∵PE//BD
∴△CEP≌△CDB
∴
∴
∴
∴S△DCP=
= ……6分
∴当m=1时,S△DEP有最大值为3,此时P(1,0) ……7分
又∵D(0,4)
又设BD的解析式y=kx+4()
将B(4,0)代入
0=4k+4
k = -1
∴BD:y= -x+4
∵PE//BD
∴设PE:y= -x+
将P(1,0)代入
0=-1+ =1
∴PE的解析式为:y= -x+1 ……8分
(3)存在
∵D(0,4) F(2,4)
CF:y=x + 2
∴M(1,3)
若 以CM为边
在y=中令y=3
x1=1+ x2=1-
∴Q1 (-2+,0) Q2(-2- ,0) ……10分
令y= -3,
x1=1+ x2=1-
Q3 (4+,0) Q4(4- ,0) ……12分
若 以CM为对角线,Q5与 Q1重合
∴共有四个点Q.
_
5
_
4
_
3
_
2
_
1
l
4题图
a
b
B
C
M
N
E
F
D
10题图
A1
O1
A2
B2
B1
C1
B
C2
A
O
D
第16题图
C
A
O
B
C
D
x
y
A
O
B
C
D
x
y
A
O
B
C
D
x
y
备用图(1)
备用图(2)
A
O
B
C
D
x
y
A
O
B
C
D
x
y
备用图(1)
H
P
E
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
