圆的标准方程
图片预览







文档简介
课件21张PPT。圆的标准方程(一)人教版第二册(上)问题情景:
山区的条件很艰苦,学校连个象样的篮球场地都没有.可孩子们自得其乐,渴望运动的他们自己动手画篮球场,可是画那个半径1.8米的中圈,和半径为6.25米的三分投蓝线难住了他们,没有那样大的圆规,怎么办?大家能帮他们想想办法吗?问题一 圆的定义是什么? 平面内到一定点的距离等于定长的点的轨迹方程是圆。定点是圆心,定长是圆的半径。 问题二 两点间距离公式是什么? 我们在前面学过,在平面直角坐标系中,两点确定一条直线,一点和倾斜角也能确定一条直线.在平面直角坐标系中,如何确定一个圆呢?复习引入问题 当圆心位置与半径大小确定后,圆就唯一确定了.
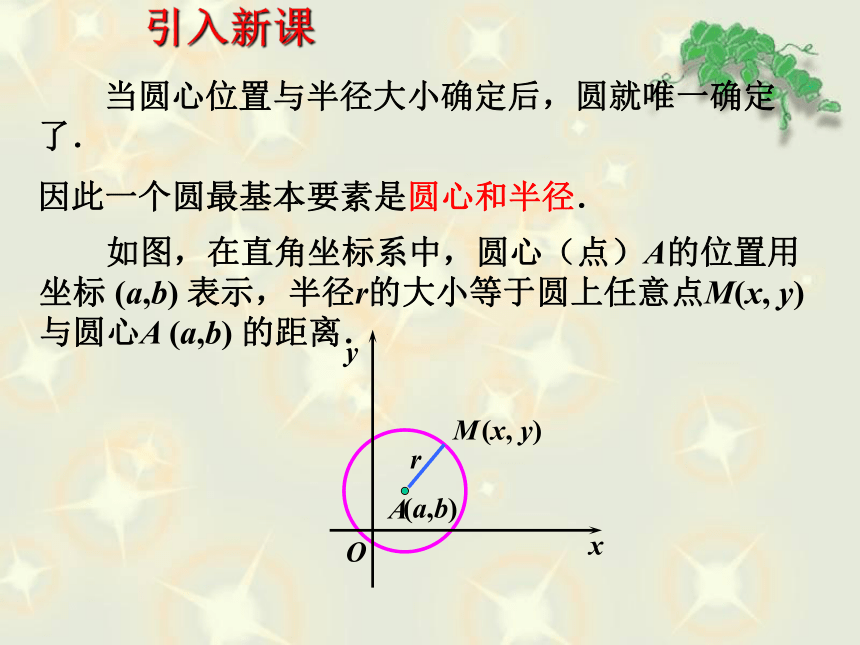
因此一个圆最基本要素是圆心和半径.引入新课 如图,在直角坐标系中,圆心(点)A的位置用坐标 (a,b) 表示,半径r的大小等于圆上任意点M(x, y)与圆心A (a,b) 的距离. 符合上述条件的圆的集合是什么?你能用描述法来表示这个集合吗?符合上述条件的圆的集合:圆的方程问题设M(x,y)是圆上任意一点, 根据定义,点M到圆心C的 距离等于r,所以圆C轨迹就是
|MC|=r
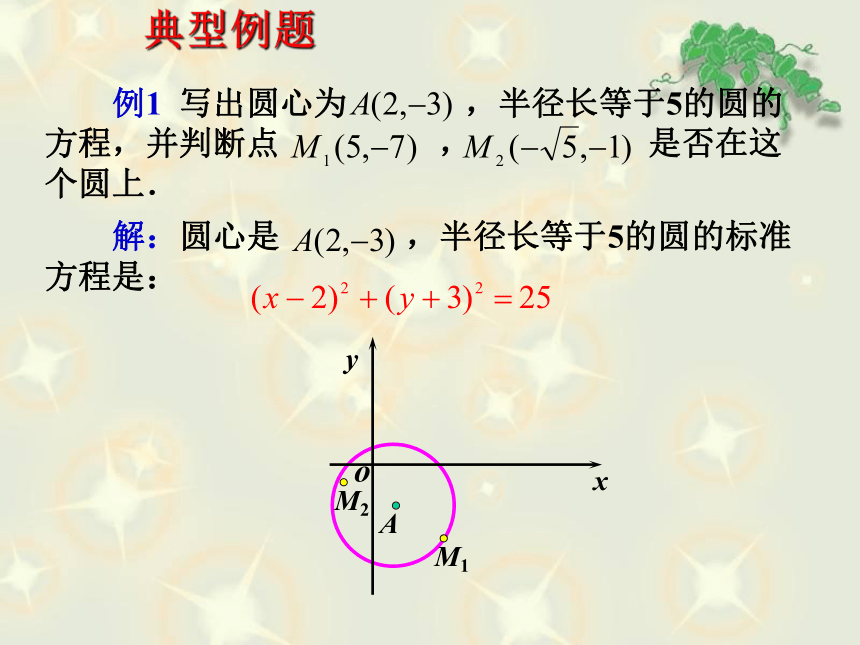
由两点间的距离公式,点M适合的条件可表示为:圆心是C(a,b),半径是 r 的圆的方程。则,所求圆的标准方程为:探究圆的标准方程: 如果圆心在原点,则圆的标准方程为:注意:圆心和半径是圆的方程的两大要素. 例1 写出圆心为 ,半径长等于5的圆的方程,并判断点 , 是否在这个圆上. 解:圆心是 ,半径长等于5的圆的标准方程是:典型例题 怎样判断点 在圆 内呢?还是在圆外呢?点与圆的位置关系探究 从上题知道,判断一个点在不在某个圆上,只需将这个点的坐标带入这个圆的方程,如果能使圆的方程成立,则在这个圆上,反之如果不成立则不在这个圆上.重要结论:
点P(x0,y0)与圆(x-a)2+(y-b)2=r2
的位置关系:点与圆的位置关系 点在圆外——点到圆心的距离大于半径 r ; 点在圆内——点到圆心的距离小于半径 r .重要结论:
点P(x0,y0)与圆(x-a)2+(y-b)2=r2
的位置关系: 例2 的三个顶点的坐标分别A(5,1), B(7,-3),C(2, -8),求它的外接圆的方程. 分析:不在同一条直线上的三个点可以确定一个圆,三角形有唯一的外接圆. 解:设所求圆的方程是 (1) 因为A(5,1), B(7,-3),C(2, -8) 都在圆上,所以它们的坐标都满足方程(1).于是例题解此方程组,得:所以, 的外接圆的方程 . 方法1 设圆方程为 则 得 方法2 确定圆心和半径 线段 AB 的垂直平方线方程为 2x-4y=16, 线段BC的垂直平方线方程为x+y=-1.解方程组 得圆心坐
标为(2,-3)关键:确定圆心坐标和半径。方法1 列出关于 方程组,解方程组得到
的值,写出圆的方程方法2 根据题设条件,求出圆心坐标和半径大小,写出圆的方程 思考1:在平面直角坐标系中有
四点,这四点能否在一个圆上?思考2:已知三条直线
两两相交,求过这三个交点的圆的方程.例3: 已知圆心为C的圆经过点A(1,1),B(2,-2),且圆心C在直线l:x-y+1=0上,求圆心为C的圆的标准方程. 分析:已知道确定一个圆只需要确定圆心的位置与半径大小.圆心为C的圆经过点A(1, 1)和B(2, -2),由于圆心C与A, B两点的距离相等,所以圆心C在线段AB的垂直平分线 上.又圆心C在直线l 上,因此圆心C是直线l与直线 的交点,半径长等于|CA|或|CB|.2.已知圆心为C 的圆经过点A(1,1)和B(2,-2)且圆心在直线l:x-y+1=0上,求圆心为C的圆的标准方程.1 设圆方程为 则 2设圆心C(a,a+1),则 3圆过A,B,则圆心C在线段AB的垂直平方线上, 得线段AB的垂直平方线方程为 x-3y-3=0.又因为C在直线 l: x-y+1=0 上,解方程组 得圆心C坐为(-3,-2)所以,圆的方程为思考1:已知 三角形AOB的顶点坐标分别是A(4,0),B(0,3)
O(0,0),求外接圆的方程.思考2:直角三角形ABC两个顶点A(4,0),B(0,3)
求直角顶点C的方程. 现有一竹筏欲载一棱长为4m的正
方体木箱通过拱洞,木箱露出水面部
分高3.8m(竹筏宽度不大于4m).
它能否顺利通过该拱桥的拱洞?圆圆的标准方程应用形数求圆的方程位置关系实际问题
山区的条件很艰苦,学校连个象样的篮球场地都没有.可孩子们自得其乐,渴望运动的他们自己动手画篮球场,可是画那个半径1.8米的中圈,和半径为6.25米的三分投蓝线难住了他们,没有那样大的圆规,怎么办?大家能帮他们想想办法吗?问题一 圆的定义是什么? 平面内到一定点的距离等于定长的点的轨迹方程是圆。定点是圆心,定长是圆的半径。 问题二 两点间距离公式是什么? 我们在前面学过,在平面直角坐标系中,两点确定一条直线,一点和倾斜角也能确定一条直线.在平面直角坐标系中,如何确定一个圆呢?复习引入问题 当圆心位置与半径大小确定后,圆就唯一确定了.
因此一个圆最基本要素是圆心和半径.引入新课 如图,在直角坐标系中,圆心(点)A的位置用坐标 (a,b) 表示,半径r的大小等于圆上任意点M(x, y)与圆心A (a,b) 的距离. 符合上述条件的圆的集合是什么?你能用描述法来表示这个集合吗?符合上述条件的圆的集合:圆的方程问题设M(x,y)是圆上任意一点, 根据定义,点M到圆心C的 距离等于r,所以圆C轨迹就是
|MC|=r
由两点间的距离公式,点M适合的条件可表示为:圆心是C(a,b),半径是 r 的圆的方程。则,所求圆的标准方程为:探究圆的标准方程: 如果圆心在原点,则圆的标准方程为:注意:圆心和半径是圆的方程的两大要素. 例1 写出圆心为 ,半径长等于5的圆的方程,并判断点 , 是否在这个圆上. 解:圆心是 ,半径长等于5的圆的标准方程是:典型例题 怎样判断点 在圆 内呢?还是在圆外呢?点与圆的位置关系探究 从上题知道,判断一个点在不在某个圆上,只需将这个点的坐标带入这个圆的方程,如果能使圆的方程成立,则在这个圆上,反之如果不成立则不在这个圆上.重要结论:
点P(x0,y0)与圆(x-a)2+(y-b)2=r2
的位置关系:点与圆的位置关系 点在圆外——点到圆心的距离大于半径 r ; 点在圆内——点到圆心的距离小于半径 r .重要结论:
点P(x0,y0)与圆(x-a)2+(y-b)2=r2
的位置关系: 例2 的三个顶点的坐标分别A(5,1), B(7,-3),C(2, -8),求它的外接圆的方程. 分析:不在同一条直线上的三个点可以确定一个圆,三角形有唯一的外接圆. 解:设所求圆的方程是 (1) 因为A(5,1), B(7,-3),C(2, -8) 都在圆上,所以它们的坐标都满足方程(1).于是例题解此方程组,得:所以, 的外接圆的方程 . 方法1 设圆方程为 则 得 方法2 确定圆心和半径 线段 AB 的垂直平方线方程为 2x-4y=16, 线段BC的垂直平方线方程为x+y=-1.解方程组 得圆心坐
标为(2,-3)关键:确定圆心坐标和半径。方法1 列出关于 方程组,解方程组得到
的值,写出圆的方程方法2 根据题设条件,求出圆心坐标和半径大小,写出圆的方程 思考1:在平面直角坐标系中有
四点,这四点能否在一个圆上?思考2:已知三条直线
两两相交,求过这三个交点的圆的方程.例3: 已知圆心为C的圆经过点A(1,1),B(2,-2),且圆心C在直线l:x-y+1=0上,求圆心为C的圆的标准方程. 分析:已知道确定一个圆只需要确定圆心的位置与半径大小.圆心为C的圆经过点A(1, 1)和B(2, -2),由于圆心C与A, B两点的距离相等,所以圆心C在线段AB的垂直平分线 上.又圆心C在直线l 上,因此圆心C是直线l与直线 的交点,半径长等于|CA|或|CB|.2.已知圆心为C 的圆经过点A(1,1)和B(2,-2)且圆心在直线l:x-y+1=0上,求圆心为C的圆的标准方程.1 设圆方程为 则 2设圆心C(a,a+1),则 3圆过A,B,则圆心C在线段AB的垂直平方线上, 得线段AB的垂直平方线方程为 x-3y-3=0.又因为C在直线 l: x-y+1=0 上,解方程组 得圆心C坐为(-3,-2)所以,圆的方程为思考1:已知 三角形AOB的顶点坐标分别是A(4,0),B(0,3)
O(0,0),求外接圆的方程.思考2:直角三角形ABC两个顶点A(4,0),B(0,3)
求直角顶点C的方程. 现有一竹筏欲载一棱长为4m的正
方体木箱通过拱洞,木箱露出水面部
分高3.8m(竹筏宽度不大于4m).
它能否顺利通过该拱桥的拱洞?圆圆的标准方程应用形数求圆的方程位置关系实际问题
