八年级数学平行四边形性质1
图片预览



文档简介
课件21张PPT。章台中学李月华数 学 八年级下册19.1.1平行四边形的性质 新人教版 观察——思考学习目标 自主探究1、平行四边形的概念及表示。
2、平行四边形的性质。
3、能用平行四边形的性质解决
问题。
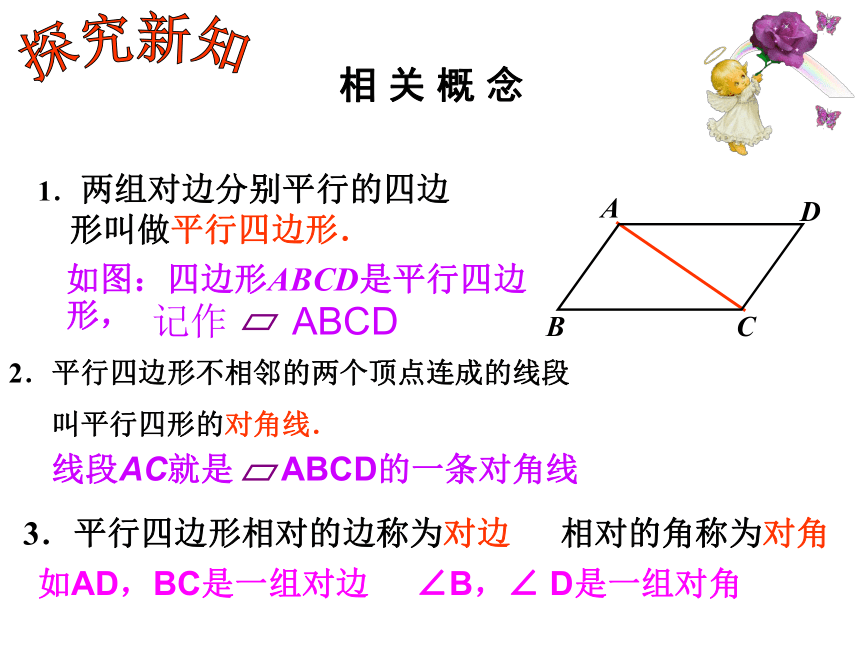
努力呦!1.两组对边分别平行的四边形叫做平行四边形.如图:四边形ABCD是平行四边形,2.平行四边形不相邻的两个顶点连成的线段
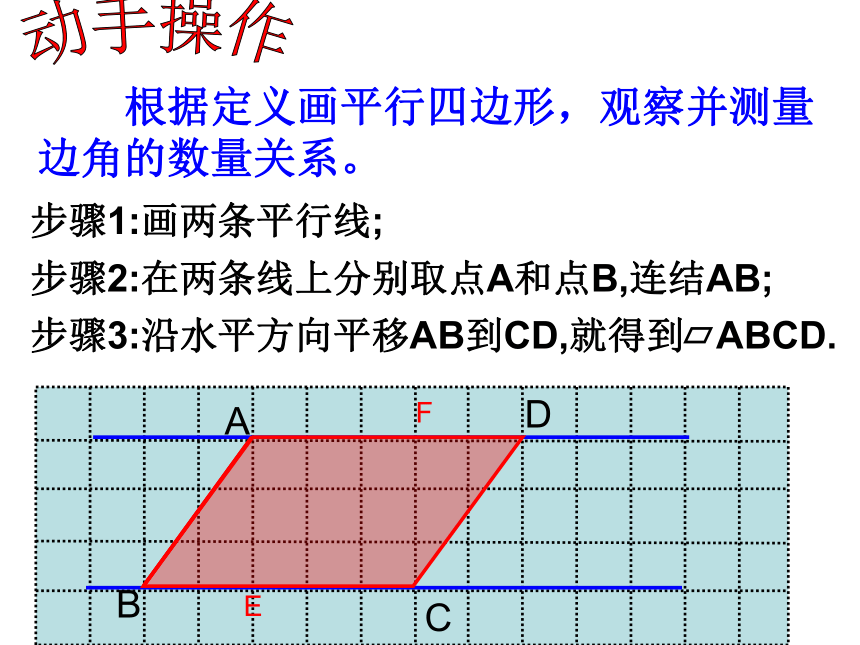
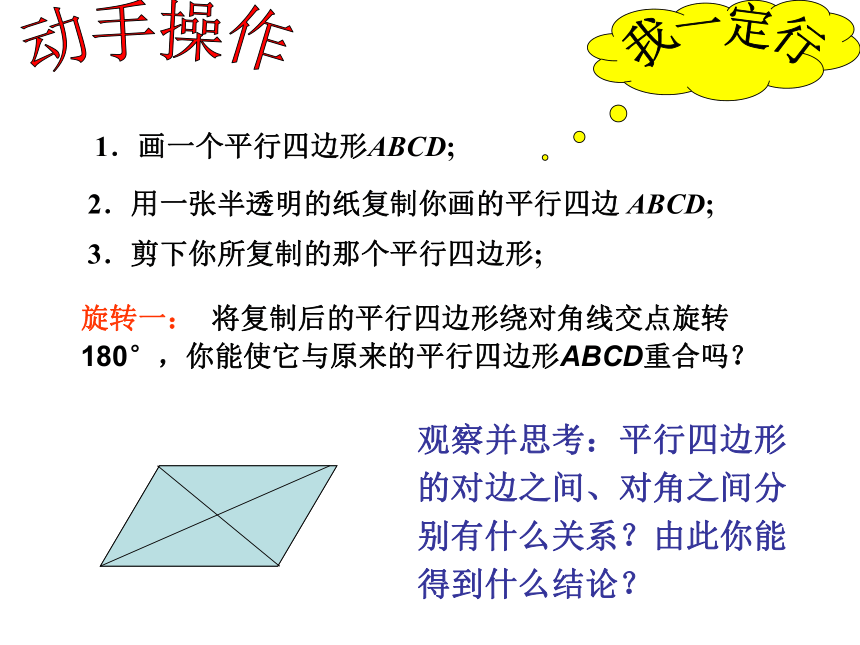
叫平行四形的对角线.3.平行四边形相对的边称为对边 相对的角称为对角相 关 概 念探究新知线段AC就是 ABCD的一条对角线如AD,BC是一组对边 ∠B,∠ D是一组对角记作 ABCDCD步骤1:画两条平行线;步骤2:在两条线上分别取点A和点B,连结AB; 根据定义画平行四边形,观察并测量边角的数量关系。动手操作EF1.画一个平行四边形ABCD;2.用一张半透明的纸复制你画的平行四边 ABCD;3.剪下你所复制的那个平行四边形;观察并思考:平行四边形的对边之间、对角之间分别有什么关系?由此你能得到什么结论? 旋转一: 将复制后的平行四边形绕对角线交点旋转 180°,你能使它与原来的平行四边形ABCD重合吗?我一定行动手操作 COBDA 在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。 -----毕达哥拉斯 对边相等
平行四边形
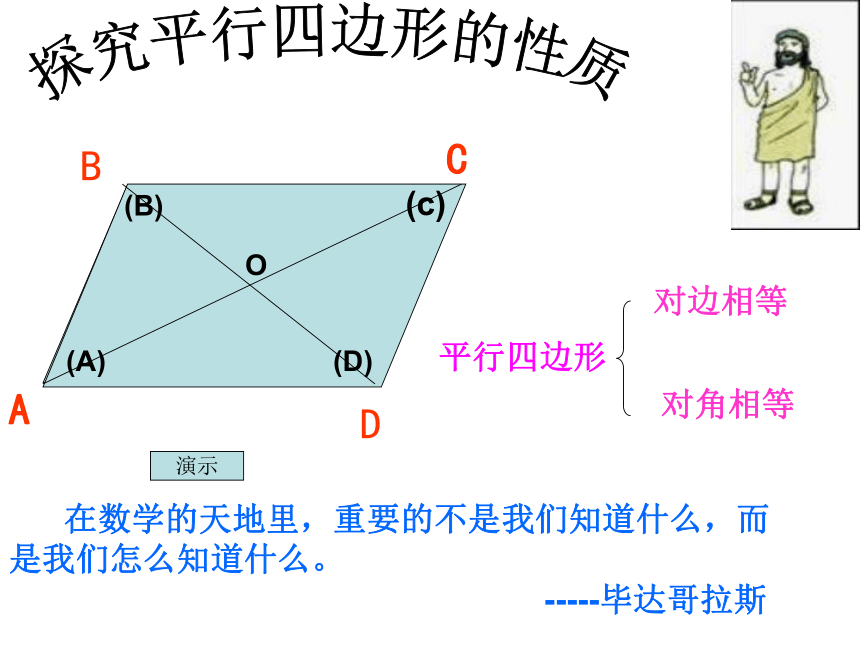
探究平行四边形的性质对角相等O演示旋转二 : 再将复制后的平行四边形绕一个顶点旋转180°.你能平移该纸片,使它与原来的平行四边形ABCD重合吗?观察并思考:平行四边形的对边之间、对角之间分别有什么关系?由此你能得到什么结论? 演 示平行四边形对边相等 对角相等探究平行四边形的性质瞧!转哩平行四边形的性质:2.平行四边形的对边相等;3.平行四边形的对角相等;
∵四边形ABCD是平行四边形∵四边形ABCD是平行四边形1.平行四边形的对边平行;∵四边形ABCD是平行四边形归纳 ∴ AB∥CD AD∥BC ∴∠A =∠ C ∠ B= ∠ D∴ AB=CD AD=BC∵四边形ABCD是平行形
∴AD∥BC ,AB∥CD
∴∠1=∠2, ∠3=∠4
又∵BD=DB
∴ △ABD≌△CDB(ASA)
∴ AB=CD AD=CB
∠A=∠C ,
∵∠1=∠2, ∠3=∠4
∴∠1+∠4=∠2+∠3
即∠ABC=∠ADC
推理证明
已知: 四边形ABCD 是平行四边形
求证: AB=CD
AD=BC
∠A= ∠ C
∠ ABC= ∠ ADCABCD)34(1()2证明:连接BD例1
如上图,小明用一根 36米长的绳子围 成了一个平行四边形的场地,其中一边AB长为8米,其他三边各长多少 ? 解: ∵四边形ABCD是平行 四边形
∴AB=CD AD=BC
∵AB+BC+CD+AD=36
∴2AB+2BC=36
∴ AB+BC=18
又∵ AB=8
∴ BC=10
∴ AD=BC=10(米)
CD=AB=8(米)
答:其他三边长是10,10,8米 ABCD 解: ∵在□ABCD中, AD∥ BC ∴ ∠A+∠B= 180° 例2 :在□ABCD中, ∠A=3∠B, 求∠C 和∠D 的度数 . 又 ∵ ∠A=3∠B
∴3∠B+∠B=∠180° 解得:∠B= 45°,
∠A=3×45°=135°
∴∠C=∠A=135 °, ∠D=∠B= 45°1、如图, ABCD中,∠B=50°则∠A= ;∠C= ;∠D= ; 2、如图, ABCD中,BC=7, AB=5,它的周长为_________.130°130°50°24反馈检测 3. 如图所示, ABCD中,若BE平分∠ABC,求ED=?
5cm
)1)2BACD9cm如果 ∠C= 100° ,求∠BED= ?3(反馈检测E解1) 在 ABCD中
AD = BC=9 AD∥BC
∴∠3=∠2
又∵ BE平分∠ABC
∴∠1=∠2 ∴∠3= ∠ 1
∴AE=AB=5
∴ED=AD-AE=9-5=4(cm)
2) 在 ABCD中
∵ ∠A =∠C=100°
又 AE=AB
∴∠1= ∠3=
(180 °- ∠A )÷2
=40°
∠BED=180°- ∠3=
180 ° - 40 °=140°
3. 如图所示,在 ABCD中,AB=5cm BC=9cm
BE平分∠ABC,求ED
如果 ∠C= 100° ,
求∠BED
ABCDE)1)23(5cm9cm小结定 义表示方法性 质两组对边分别平行的四边形叫做平行四边形。其不相邻的两个顶点连成的线段叫它的对角线。平行四边形ABCD, 记为“□ABCD ”, 读作“平行四边形ABCD”, 其中线段AC, BD 称为对角线。平行四边形的对边相等,对角相等.性 质 应 用例题及反馈检测 作 业
P90页:
习题19.1,第1、第2拓展延伸你能画一条直线将一个平行四边形分成两个形状和大小完全相同的两部分吗?
试一试,这样的直线你能画几条?
2、平行四边形的性质。
3、能用平行四边形的性质解决
问题。
努力呦!1.两组对边分别平行的四边形叫做平行四边形.如图:四边形ABCD是平行四边形,2.平行四边形不相邻的两个顶点连成的线段
叫平行四形的对角线.3.平行四边形相对的边称为对边 相对的角称为对角相 关 概 念探究新知线段AC就是 ABCD的一条对角线如AD,BC是一组对边 ∠B,∠ D是一组对角记作 ABCDCD步骤1:画两条平行线;步骤2:在两条线上分别取点A和点B,连结AB; 根据定义画平行四边形,观察并测量边角的数量关系。动手操作EF1.画一个平行四边形ABCD;2.用一张半透明的纸复制你画的平行四边 ABCD;3.剪下你所复制的那个平行四边形;观察并思考:平行四边形的对边之间、对角之间分别有什么关系?由此你能得到什么结论? 旋转一: 将复制后的平行四边形绕对角线交点旋转 180°,你能使它与原来的平行四边形ABCD重合吗?我一定行动手操作 COBDA 在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。 -----毕达哥拉斯 对边相等
平行四边形
探究平行四边形的性质对角相等O演示旋转二 : 再将复制后的平行四边形绕一个顶点旋转180°.你能平移该纸片,使它与原来的平行四边形ABCD重合吗?观察并思考:平行四边形的对边之间、对角之间分别有什么关系?由此你能得到什么结论? 演 示平行四边形对边相等 对角相等探究平行四边形的性质瞧!转哩平行四边形的性质:2.平行四边形的对边相等;3.平行四边形的对角相等;
∵四边形ABCD是平行四边形∵四边形ABCD是平行四边形1.平行四边形的对边平行;∵四边形ABCD是平行四边形归纳 ∴ AB∥CD AD∥BC ∴∠A =∠ C ∠ B= ∠ D∴ AB=CD AD=BC∵四边形ABCD是平行形
∴AD∥BC ,AB∥CD
∴∠1=∠2, ∠3=∠4
又∵BD=DB
∴ △ABD≌△CDB(ASA)
∴ AB=CD AD=CB
∠A=∠C ,
∵∠1=∠2, ∠3=∠4
∴∠1+∠4=∠2+∠3
即∠ABC=∠ADC
推理证明
已知: 四边形ABCD 是平行四边形
求证: AB=CD
AD=BC
∠A= ∠ C
∠ ABC= ∠ ADCABCD)34(1()2证明:连接BD例1
如上图,小明用一根 36米长的绳子围 成了一个平行四边形的场地,其中一边AB长为8米,其他三边各长多少 ? 解: ∵四边形ABCD是平行 四边形
∴AB=CD AD=BC
∵AB+BC+CD+AD=36
∴2AB+2BC=36
∴ AB+BC=18
又∵ AB=8
∴ BC=10
∴ AD=BC=10(米)
CD=AB=8(米)
答:其他三边长是10,10,8米 ABCD 解: ∵在□ABCD中, AD∥ BC ∴ ∠A+∠B= 180° 例2 :在□ABCD中, ∠A=3∠B, 求∠C 和∠D 的度数 . 又 ∵ ∠A=3∠B
∴3∠B+∠B=∠180° 解得:∠B= 45°,
∠A=3×45°=135°
∴∠C=∠A=135 °, ∠D=∠B= 45°1、如图, ABCD中,∠B=50°则∠A= ;∠C= ;∠D= ; 2、如图, ABCD中,BC=7, AB=5,它的周长为_________.130°130°50°24反馈检测 3. 如图所示, ABCD中,若BE平分∠ABC,求ED=?
5cm
)1)2BACD9cm如果 ∠C= 100° ,求∠BED= ?3(反馈检测E解1) 在 ABCD中
AD = BC=9 AD∥BC
∴∠3=∠2
又∵ BE平分∠ABC
∴∠1=∠2 ∴∠3= ∠ 1
∴AE=AB=5
∴ED=AD-AE=9-5=4(cm)
2) 在 ABCD中
∵ ∠A =∠C=100°
又 AE=AB
∴∠1= ∠3=
(180 °- ∠A )÷2
=40°
∠BED=180°- ∠3=
180 ° - 40 °=140°
3. 如图所示,在 ABCD中,AB=5cm BC=9cm
BE平分∠ABC,求ED
如果 ∠C= 100° ,
求∠BED
ABCDE)1)23(5cm9cm小结定 义表示方法性 质两组对边分别平行的四边形叫做平行四边形。其不相邻的两个顶点连成的线段叫它的对角线。平行四边形ABCD, 记为“□ABCD ”, 读作“平行四边形ABCD”, 其中线段AC, BD 称为对角线。平行四边形的对边相等,对角相等.性 质 应 用例题及反馈检测 作 业
P90页:
习题19.1,第1、第2拓展延伸你能画一条直线将一个平行四边形分成两个形状和大小完全相同的两部分吗?
试一试,这样的直线你能画几条?
