17.3可化为一元一次方程的分式方程
文档属性
| 名称 | 17.3可化为一元一次方程的分式方程 |  | |
| 格式 | rar | ||
| 文件大小 | 413.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-02-22 21:55:00 | ||
图片预览






文档简介
课件23张PPT。17.3 可化为一元一次方程的
分式方程问题引入 轮船在顺水中航行80千米所需的时间和
逆水航行60千米所需的时间相同.已知水流的
速度是3千米/时,求轮船在静水中的速度.分析:设轮船在静水中的速度为x千米/时,
根据题意,得(1)问题引入 甲加工180个零件的时间与乙加工240个
零件的时间相同,已知甲每小时比乙少加工
5个零件,求两人每小时各加工多少个零件?分析:设甲每小时加工x个零件,
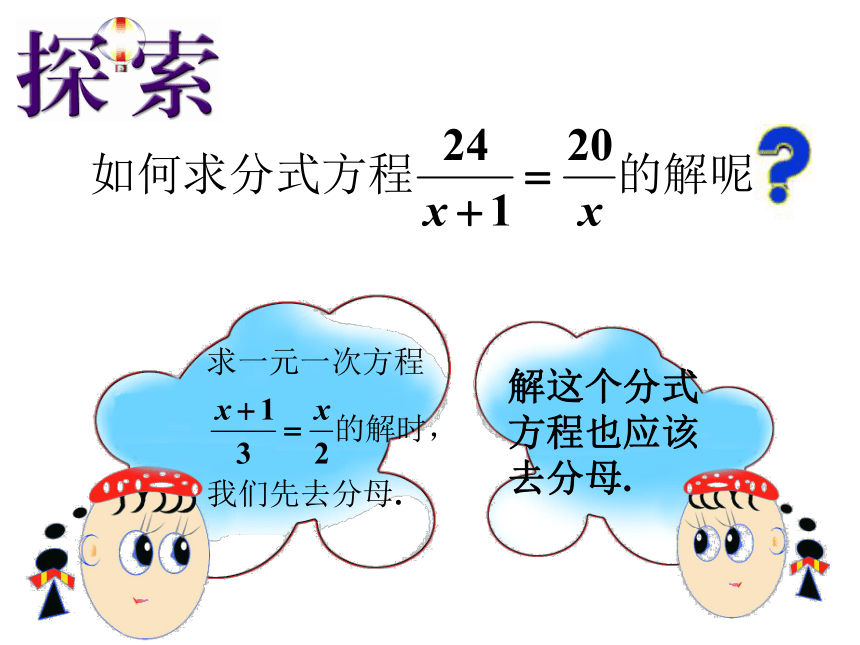
根据题意得:(2)(1)(2)1、以下两个方程有什么共同特点?
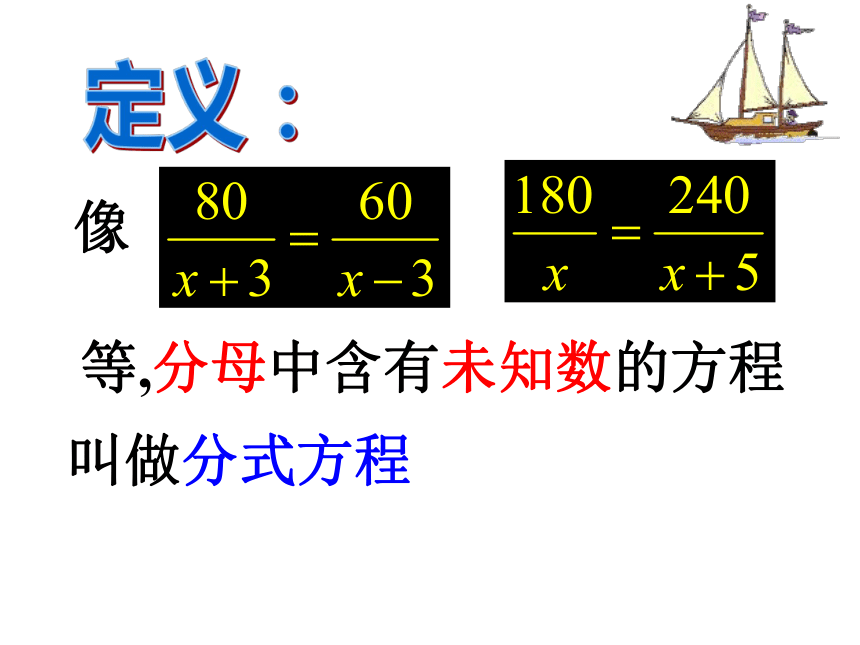
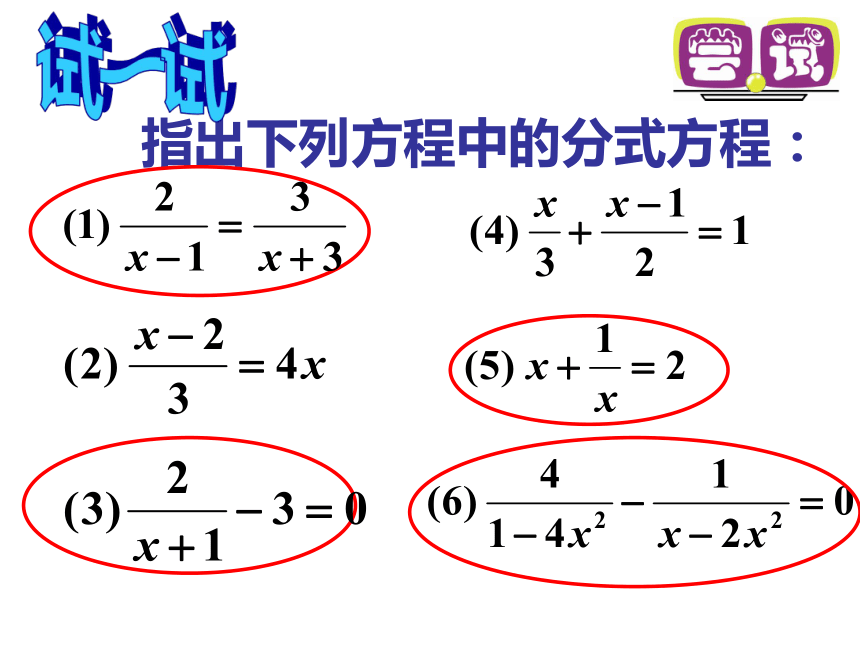
2、属于什么方程?阅读课本P11~P13,并解答下列问题:定义: 等,分母中含有未知数的方程叫做分式方程像指出下列方程中的分式方程:试一试解:方程两边同乘以(x+3)(x-3),约去分母,得80(x-3)=60(x+3)解这个方程,得 x=21解分式方程的基本思想将 方程转
化为整式方程.分式例1 解方程:解:方程两边同乘以(x+1)(x-1),约去分母,得X+1=2.解这个整式方程,得 x=1.这就是方程的解了吗?检验:把x=1代入(x+1)(x-1),得(1+1)×(1-1)=0所以原分式方程无解这是原分式方程的增根.例2 解方程:解:方程两边同乘以x(x-7),约去分母,得100(x-7)=30x解这个整式方程,得 x=10.检验:把x=10代入x(x-7),得10×(10-7)≠0所以,x=10是原方程的解.总结一. 通过例题的讲解和练习的操作,你能总结出解分式方程的一般步骤吗?解分式方程的一般步骤:
在方程的两边都乘以最简公分母,化成____________方程;
解这个____________方程;
检验:把__________方程的根代入____________.如果值_________,就是原方程的根;如果值__________,就是增根.应当__________.
随堂练习解方程:说一说收获和体会课堂练习:
(1)
?
(2)解:在方程两边都乘以x(x-1)得
3(x-1)+6x=x+m所以8x-m-3=0.因为方程的增根是x=0或x=1所以m= -3或m=5.知识拓展6.关于x的方程有增根,则k=_____.随堂练习知识拓展2、若关于x的方程
有增根,则增根是 ( )
知识拓展3.a为何值时关于x的方程的解是零.4.的根是( )5.方程的增根是( )。小结:分式分母分式增根练习二
分式方程问题引入 轮船在顺水中航行80千米所需的时间和
逆水航行60千米所需的时间相同.已知水流的
速度是3千米/时,求轮船在静水中的速度.分析:设轮船在静水中的速度为x千米/时,
根据题意,得(1)问题引入 甲加工180个零件的时间与乙加工240个
零件的时间相同,已知甲每小时比乙少加工
5个零件,求两人每小时各加工多少个零件?分析:设甲每小时加工x个零件,
根据题意得:(2)(1)(2)1、以下两个方程有什么共同特点?
2、属于什么方程?阅读课本P11~P13,并解答下列问题:定义: 等,分母中含有未知数的方程叫做分式方程像指出下列方程中的分式方程:试一试解:方程两边同乘以(x+3)(x-3),约去分母,得80(x-3)=60(x+3)解这个方程,得 x=21解分式方程的基本思想将 方程转
化为整式方程.分式例1 解方程:解:方程两边同乘以(x+1)(x-1),约去分母,得X+1=2.解这个整式方程,得 x=1.这就是方程的解了吗?检验:把x=1代入(x+1)(x-1),得(1+1)×(1-1)=0所以原分式方程无解这是原分式方程的增根.例2 解方程:解:方程两边同乘以x(x-7),约去分母,得100(x-7)=30x解这个整式方程,得 x=10.检验:把x=10代入x(x-7),得10×(10-7)≠0所以,x=10是原方程的解.总结一. 通过例题的讲解和练习的操作,你能总结出解分式方程的一般步骤吗?解分式方程的一般步骤:
在方程的两边都乘以最简公分母,化成____________方程;
解这个____________方程;
检验:把__________方程的根代入____________.如果值_________,就是原方程的根;如果值__________,就是增根.应当__________.
随堂练习解方程:说一说收获和体会课堂练习:
(1)
?
(2)解:在方程两边都乘以x(x-1)得
3(x-1)+6x=x+m所以8x-m-3=0.因为方程的增根是x=0或x=1所以m= -3或m=5.知识拓展6.关于x的方程有增根,则k=_____.随堂练习知识拓展2、若关于x的方程
有增根,则增根是 ( )
知识拓展3.a为何值时关于x的方程的解是零.4.的根是( )5.方程的增根是( )。小结:分式分母分式增根练习二
