测试题人教a版必修一:第一章集合与函数的概念测试卷(1)
文档属性
| 名称 | 测试题人教a版必修一:第一章集合与函数的概念测试卷(1) |  | |
| 格式 | zip | ||
| 文件大小 | 73.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-02-22 10:19:00 | ||
图片预览


文档简介
必修一数学第一章集合与函数的概念测试卷
一.选择题(每小题4分,满分40分。把答案填在答题卷上相应的表格中)
1.若,则
A B C D
2.下列四组函数,表示同一函数的是 ( )
(A)f (x)=, g(x)=x (B) f (x)=x, g(x)=
(C)f (x)=, g(x)= (D)f (x)=|x+1|, g(x)=
3.如果集合A={x|ax2+2x+1=0}中只有一个元素,则a的值是 ( )
A.0 B.0 或1 C.1 D.不能确定
4.在映射,,且,则与A中的元素对应的B中的元素为( )
(A) (B) (C) (D)
5. 如果奇函数f(x)在区间[3,7]上是增函数且最小值为5,那么f(x)在区间
[-7,-3]上是( )
(A)增函数且最大值为-5 (B)增函数且最小值为-5
(C)减函数且最小值为-5 (D)减函数且最大值为-5
6.如图,阴影部分表示的集合是 ( )
(A)B∩[CU (A∪C)] (B)(A∪B)∪(B∪C)
(C)(A∪C)∩( CUB) (D)[CU (A∩C)]∪B
7.函数是定义域为R的奇函数,当时,,则当时,的表达式为 ( )
A. B. C. D.
8.函数y=是
A.奇函数 B.偶函数 C.既是奇函数又是偶函数 D.非奇非偶数
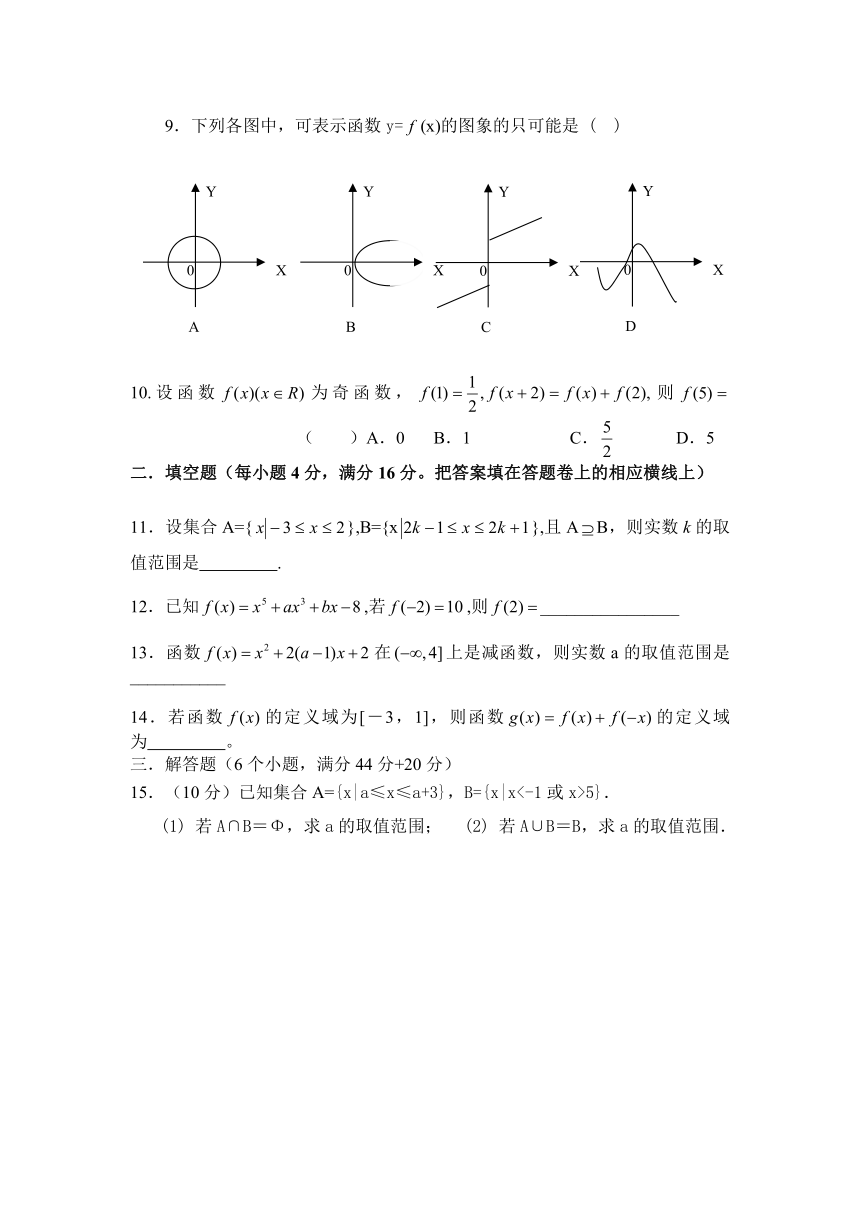
9.下列各图中,可表示函数y=(x)的图象的只可能是 ( )
10.设函数为奇函数,则 ( )A.0 B.1 C. D.5
二.填空题(每小题4分,满分16分。把答案填在答题卷上的相应横线上)
11.设集合A={},B={x},且AB,则实数k的取值范围是 .
12.已知,若,则________________
13.函数在上是减函数,则实数a的取值范围是___________
14.若函数的定义域为[-3,1],则函数的定义域为 。
三.解答题(6个小题,满分44分+20分)
15.(10分)已知集合A={x|a≤x≤a+3},B={x|x<-1或x>5}.
(1) 若A∩B=Φ,求a的取值范围; (2) 若A∪B=B,求a的取值范围.
16.(10分)已知f(x)= ,求f[f(0)]的值.
17.(12分)已知函数是奇函数,且.
(1)求函数f(x)的解析式;
(2)判断函数f(x)在上的单调性,并加以证明.
18.(12分)定义在R上的函数,对任意的,有
,且。
求证: ; (2)求证:是偶函数。
附加题:19.(10分)若是定义在上的增函数,且
⑴求的值;⑵若,解不等式
附加题:20.(10分)已知≤≤1,若函数在区间[1,3]上的最大值为,最小值为,令.
(1)求的函数表达式;
(2)判断函数在区间[,1]上的单调性,并求出的最小值 .
数学参考答案及评分标准
一.选择题(每小题4分,满分40分。把答案填在下面的表格中)
题目 1 2 3 4 5 6 7 8 9 10
答案 D D B A A A B B D C
二.填空题(每小题4分,满分16分。把答案填在下面的横线上)
11.{} 12 13 1 4
三.解答题(6个小题,满分44分+20分)
15.(满分10分)答案:(1) (2)
16(满分10分).解: ∵ 0(-), ∴f(0)=,又>1,
∴ f()=()3+()-3=2+=,即f[f(0)]=.
17.(满分12分)已知函数是奇函数,且.
(1)求函数f(x)的解析式;
(2)判断函数f(x)在上的单调性,并加以证明.
解:(1)∵f(x)是奇函数,∴对定义域内的任意的x,都有,
即,整理得: ∴q=0 ………2分
又∵,∴,
解得p=2 …………………………………………4分
∴所求解析式为 …………………………………………5分
(2)由(1)可得=,
设,
则由于
=………9分
因此,当时,,
从而得到即,
∴是f(x)的递增区间。 ………………………12分
18.(满分12分) (1)证明:取,, ∵ ∴
(2)证明:取,,
∵ , ∴,即
∴是偶函数。
19.(满分10分)解:⑴在等式中令,则;
⑵在等式中令则,,
故原不等式为:即,
又在上为增函数,故原不等式等价于:
20.(满分10分)解:(1)∵的图像为开口向上的抛物线,且对称轴为
∴有最小值 .
当2≤≤3时,[有最大值;
当1≤<2时,a∈(有最大值M(a)=f(3)=9a-5;
(2)设则
上是减函数.
设 则
上是增函数.∴当时,有最小值.
0
X
Y
A
0
X
Y
B
0
X
Y
C
0
X
Y
D
一.选择题(每小题4分,满分40分。把答案填在答题卷上相应的表格中)
1.若,则
A B C D
2.下列四组函数,表示同一函数的是 ( )
(A)f (x)=, g(x)=x (B) f (x)=x, g(x)=
(C)f (x)=, g(x)= (D)f (x)=|x+1|, g(x)=
3.如果集合A={x|ax2+2x+1=0}中只有一个元素,则a的值是 ( )
A.0 B.0 或1 C.1 D.不能确定
4.在映射,,且,则与A中的元素对应的B中的元素为( )
(A) (B) (C) (D)
5. 如果奇函数f(x)在区间[3,7]上是增函数且最小值为5,那么f(x)在区间
[-7,-3]上是( )
(A)增函数且最大值为-5 (B)增函数且最小值为-5
(C)减函数且最小值为-5 (D)减函数且最大值为-5
6.如图,阴影部分表示的集合是 ( )
(A)B∩[CU (A∪C)] (B)(A∪B)∪(B∪C)
(C)(A∪C)∩( CUB) (D)[CU (A∩C)]∪B
7.函数是定义域为R的奇函数,当时,,则当时,的表达式为 ( )
A. B. C. D.
8.函数y=是
A.奇函数 B.偶函数 C.既是奇函数又是偶函数 D.非奇非偶数
9.下列各图中,可表示函数y=(x)的图象的只可能是 ( )
10.设函数为奇函数,则 ( )A.0 B.1 C. D.5
二.填空题(每小题4分,满分16分。把答案填在答题卷上的相应横线上)
11.设集合A={},B={x},且AB,则实数k的取值范围是 .
12.已知,若,则________________
13.函数在上是减函数,则实数a的取值范围是___________
14.若函数的定义域为[-3,1],则函数的定义域为 。
三.解答题(6个小题,满分44分+20分)
15.(10分)已知集合A={x|a≤x≤a+3},B={x|x<-1或x>5}.
(1) 若A∩B=Φ,求a的取值范围; (2) 若A∪B=B,求a的取值范围.
16.(10分)已知f(x)= ,求f[f(0)]的值.
17.(12分)已知函数是奇函数,且.
(1)求函数f(x)的解析式;
(2)判断函数f(x)在上的单调性,并加以证明.
18.(12分)定义在R上的函数,对任意的,有
,且。
求证: ; (2)求证:是偶函数。
附加题:19.(10分)若是定义在上的增函数,且
⑴求的值;⑵若,解不等式
附加题:20.(10分)已知≤≤1,若函数在区间[1,3]上的最大值为,最小值为,令.
(1)求的函数表达式;
(2)判断函数在区间[,1]上的单调性,并求出的最小值 .
数学参考答案及评分标准
一.选择题(每小题4分,满分40分。把答案填在下面的表格中)
题目 1 2 3 4 5 6 7 8 9 10
答案 D D B A A A B B D C
二.填空题(每小题4分,满分16分。把答案填在下面的横线上)
11.{} 12 13 1 4
三.解答题(6个小题,满分44分+20分)
15.(满分10分)答案:(1) (2)
16(满分10分).解: ∵ 0(-), ∴f(0)=,又>1,
∴ f()=()3+()-3=2+=,即f[f(0)]=.
17.(满分12分)已知函数是奇函数,且.
(1)求函数f(x)的解析式;
(2)判断函数f(x)在上的单调性,并加以证明.
解:(1)∵f(x)是奇函数,∴对定义域内的任意的x,都有,
即,整理得: ∴q=0 ………2分
又∵,∴,
解得p=2 …………………………………………4分
∴所求解析式为 …………………………………………5分
(2)由(1)可得=,
设,
则由于
=………9分
因此,当时,,
从而得到即,
∴是f(x)的递增区间。 ………………………12分
18.(满分12分) (1)证明:取,, ∵ ∴
(2)证明:取,,
∵ , ∴,即
∴是偶函数。
19.(满分10分)解:⑴在等式中令,则;
⑵在等式中令则,,
故原不等式为:即,
又在上为增函数,故原不等式等价于:
20.(满分10分)解:(1)∵的图像为开口向上的抛物线,且对称轴为
∴有最小值 .
当2≤≤3时,[有最大值;
当1≤<2时,a∈(有最大值M(a)=f(3)=9a-5;
(2)设则
上是减函数.
设 则
上是增函数.∴当时,有最小值.
0
X
Y
A
0
X
Y
B
0
X
Y
C
0
X
Y
D
