测试题新人教a版必修二:第一章 空间几何体测试卷3
文档属性
| 名称 | 测试题新人教a版必修二:第一章 空间几何体测试卷3 |  | |
| 格式 | zip | ||
| 文件大小 | 72.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-02-22 10:20:00 | ||
图片预览

文档简介
空间几何体 单元测试
( 时间 100分钟 总分 100分)
班级_______________ 姓名______________ 分数_____________
一、选择题(每小题4分,共40分)
1、正方体的内切球和外接球的半径之比为
A B C D
2、一个棱柱是正四棱柱的条件是
A 底面是正方形,有两个侧面是矩形 B 底面是正方形,有两个侧面垂直于底面
C 底面是菱形,且有一个顶点处的三条棱两两垂直 D 每个侧面都是全等矩形的四棱柱
3、过圆锥的高的三等分点作平行于底面的截面,它们把圆锥侧面分成的三部分
的面积之比为
A 1:2:3 B 1:3:5 C 1:2:4 D 1:3:9
4、已知正方形的直观图是有一条边长为4的平行四边形,则此正方形的面积是
A 16 B 16或64 C 64 D 都不对
5、下列说法正确的是
A 圆锥的侧面展开图是一个等腰三角形
B 棱柱即是两个底面全等且其余各面都是矩形的多面体
C 任何一个棱台都可以补一个棱锥使它们组成一个新的棱锥
D 通过圆台侧面上一点,有无数条母线
6、圆锥的轴截面是等腰直角三角形,侧面积是,则圆锥的体积是
A B C D
7、若一棱锥的底面积是8,则这个棱锥的中截面(过棱锥高的中点且平行于底面的截面)的面积是
A 4 B C 2 D
8、若一圆柱的侧面展开图是一个正方形,则这个圆柱的全面积和侧面积之比是
A B C D
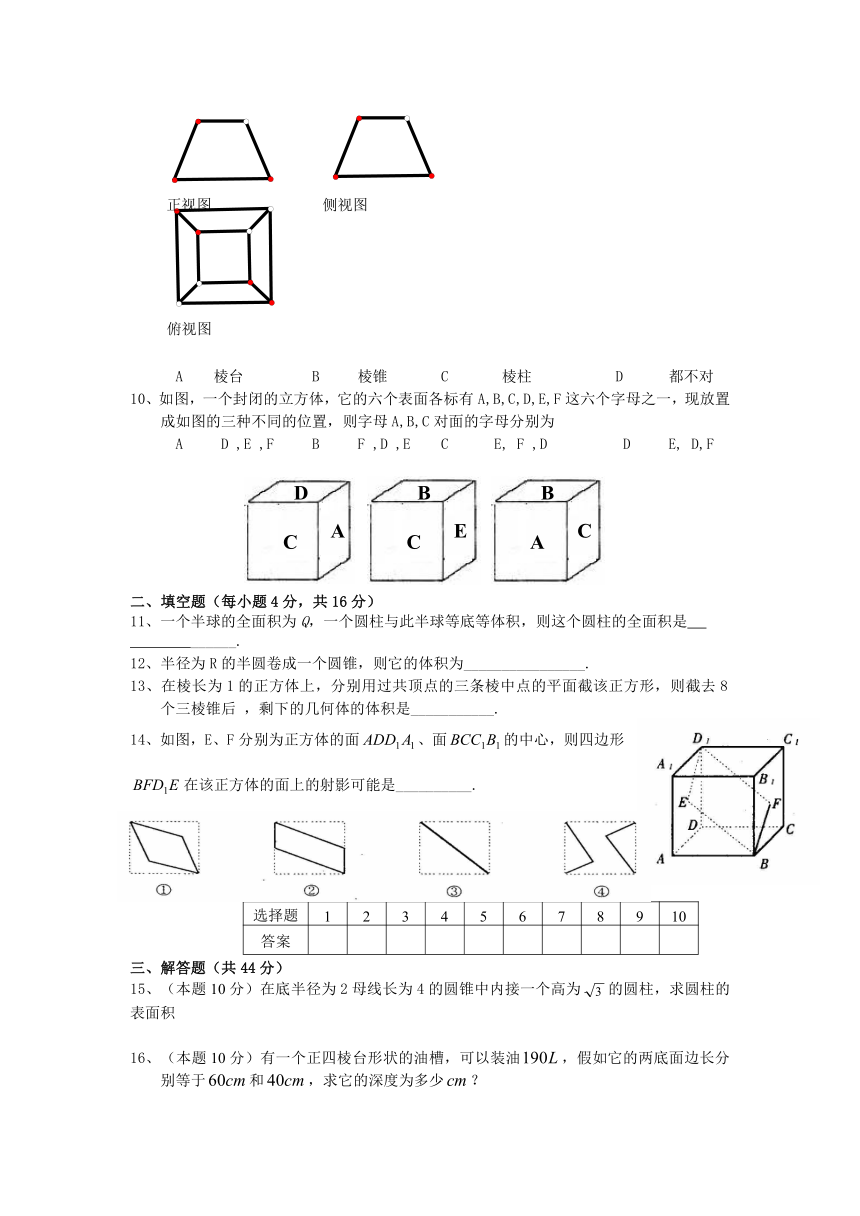
9、有一个几何体的三视图如下图所示,这个几何体应是一个
A 棱台 B 棱锥 C 棱柱 D 都不对
10、如图,一个封闭的立方体,它的六个表面各标有A,B,C,D,E,F这六个字母之一,现放置成如图的三种不同的位置,则字母A,B,C对面的字母分别为
A D ,E ,F B F ,D ,E C E, F ,D D E, D,F
二、填空题(每小题4分,共16分)
11、一个半球的全面积为Q,一个圆柱与此半球等底等体积,则这个圆柱的全面积是 ______.
12、半径为R的半圆卷成一个圆锥,则它的体积为________________.
13、在棱长为1的正方体上,分别用过共顶点的三条棱中点的平面截该正方形,则截去8个三棱锥后 ,剩下的几何体的体积是___________.
14、如图,E、F分别为正方体的面、面的中心,则四边形 在该正方体的面上的射影可能是__________.
选择题 1 2 3 4 5 6 7 8 9 10
答案
三、解答题(共44分)
15、(本题10分)在底半径为2母线长为4的圆锥中内接一个高为的圆柱,求圆柱的表面积
16、(本题10分)有一个正四棱台形状的油槽,可以装油,假如它的两底面边长分别等于和,求它的深度为多少?
17、(本题12分)一个三棱柱的底面是3的正三角形,侧棱垂直于底面,它的三视图如图所示,.
(1)请画出它的直观图;(2)求这个三棱柱的表面积和体积.
18、(本题12分)养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12M,高4M。养路处拟建一个更大的圆锥形仓库,以存放更多食盐。现有两种方案:一是新建的仓库的底面直径比原来大4M(高不变);二是高度增加4M(底面直径不变)。
分别计算按这两种方案所建的仓库的体积;
分别计算按这两种方案所建的仓库的表面积;
哪个方案更经济些?
参考答案
1-10题 DDBBC ACAAD; 11、;12、;13、;14、②③;15、R=1,h=,S=2+2;
16、解:由题意有,.
.
∴.
17、解:(1)略;(2)S=27+;V=.
18、解:(1)如果按方案一,仓库的底面直径变成16M,则仓库的体积
如果按方案二,仓库的高变成8M,则仓库的体积
(2)如果按方案一,仓库的底面直径变成16M,半径为8M.
棱锥的母线长为
则仓库的表面积
如果按方案二,仓库的高变成8M.
棱锥的母线长为
则仓库的表面积
(3) ,
俯视图
侧视图
正视图
C
B
A
A
D
C
E
B
C
A
B
A1
B1
C
C1
正视图
侧视图
府视图
( 时间 100分钟 总分 100分)
班级_______________ 姓名______________ 分数_____________
一、选择题(每小题4分,共40分)
1、正方体的内切球和外接球的半径之比为
A B C D
2、一个棱柱是正四棱柱的条件是
A 底面是正方形,有两个侧面是矩形 B 底面是正方形,有两个侧面垂直于底面
C 底面是菱形,且有一个顶点处的三条棱两两垂直 D 每个侧面都是全等矩形的四棱柱
3、过圆锥的高的三等分点作平行于底面的截面,它们把圆锥侧面分成的三部分
的面积之比为
A 1:2:3 B 1:3:5 C 1:2:4 D 1:3:9
4、已知正方形的直观图是有一条边长为4的平行四边形,则此正方形的面积是
A 16 B 16或64 C 64 D 都不对
5、下列说法正确的是
A 圆锥的侧面展开图是一个等腰三角形
B 棱柱即是两个底面全等且其余各面都是矩形的多面体
C 任何一个棱台都可以补一个棱锥使它们组成一个新的棱锥
D 通过圆台侧面上一点,有无数条母线
6、圆锥的轴截面是等腰直角三角形,侧面积是,则圆锥的体积是
A B C D
7、若一棱锥的底面积是8,则这个棱锥的中截面(过棱锥高的中点且平行于底面的截面)的面积是
A 4 B C 2 D
8、若一圆柱的侧面展开图是一个正方形,则这个圆柱的全面积和侧面积之比是
A B C D
9、有一个几何体的三视图如下图所示,这个几何体应是一个
A 棱台 B 棱锥 C 棱柱 D 都不对
10、如图,一个封闭的立方体,它的六个表面各标有A,B,C,D,E,F这六个字母之一,现放置成如图的三种不同的位置,则字母A,B,C对面的字母分别为
A D ,E ,F B F ,D ,E C E, F ,D D E, D,F
二、填空题(每小题4分,共16分)
11、一个半球的全面积为Q,一个圆柱与此半球等底等体积,则这个圆柱的全面积是 ______.
12、半径为R的半圆卷成一个圆锥,则它的体积为________________.
13、在棱长为1的正方体上,分别用过共顶点的三条棱中点的平面截该正方形,则截去8个三棱锥后 ,剩下的几何体的体积是___________.
14、如图,E、F分别为正方体的面、面的中心,则四边形 在该正方体的面上的射影可能是__________.
选择题 1 2 3 4 5 6 7 8 9 10
答案
三、解答题(共44分)
15、(本题10分)在底半径为2母线长为4的圆锥中内接一个高为的圆柱,求圆柱的表面积
16、(本题10分)有一个正四棱台形状的油槽,可以装油,假如它的两底面边长分别等于和,求它的深度为多少?
17、(本题12分)一个三棱柱的底面是3的正三角形,侧棱垂直于底面,它的三视图如图所示,.
(1)请画出它的直观图;(2)求这个三棱柱的表面积和体积.
18、(本题12分)养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12M,高4M。养路处拟建一个更大的圆锥形仓库,以存放更多食盐。现有两种方案:一是新建的仓库的底面直径比原来大4M(高不变);二是高度增加4M(底面直径不变)。
分别计算按这两种方案所建的仓库的体积;
分别计算按这两种方案所建的仓库的表面积;
哪个方案更经济些?
参考答案
1-10题 DDBBC ACAAD; 11、;12、;13、;14、②③;15、R=1,h=,S=2+2;
16、解:由题意有,.
.
∴.
17、解:(1)略;(2)S=27+;V=.
18、解:(1)如果按方案一,仓库的底面直径变成16M,则仓库的体积
如果按方案二,仓库的高变成8M,则仓库的体积
(2)如果按方案一,仓库的底面直径变成16M,半径为8M.
棱锥的母线长为
则仓库的表面积
如果按方案二,仓库的高变成8M.
棱锥的母线长为
则仓库的表面积
(3) ,
俯视图
侧视图
正视图
C
B
A
A
D
C
E
B
C
A
B
A1
B1
C
C1
正视图
侧视图
府视图
