函数奇偶性
图片预览




文档简介
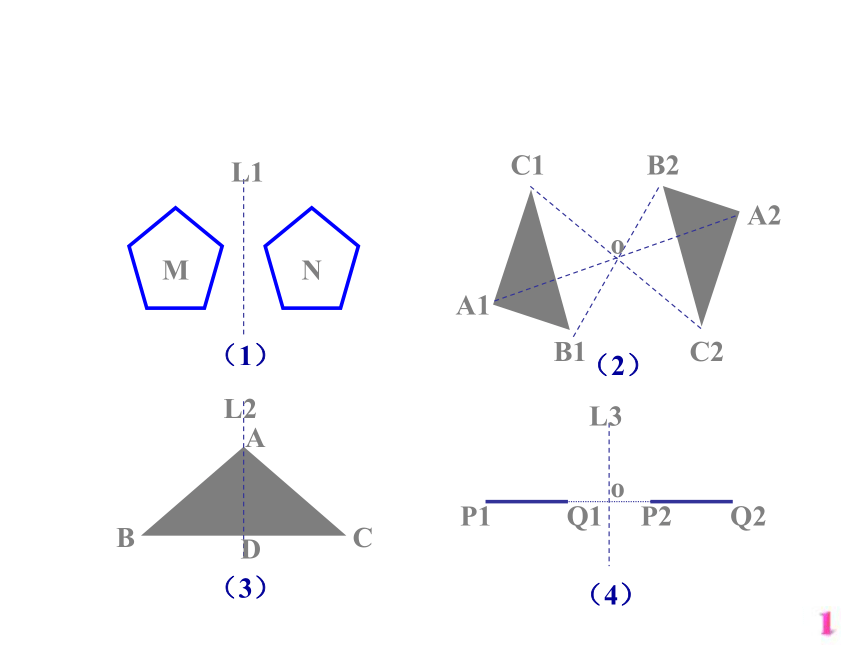
课件22张PPT。函数的奇偶性MN(1)(2)(3)(4)A1B2C2oA2B1L1L2L3ABCDC1P1P2Q1Q2o自学提纲1 什么是奇函数?
2 什么是偶函数?
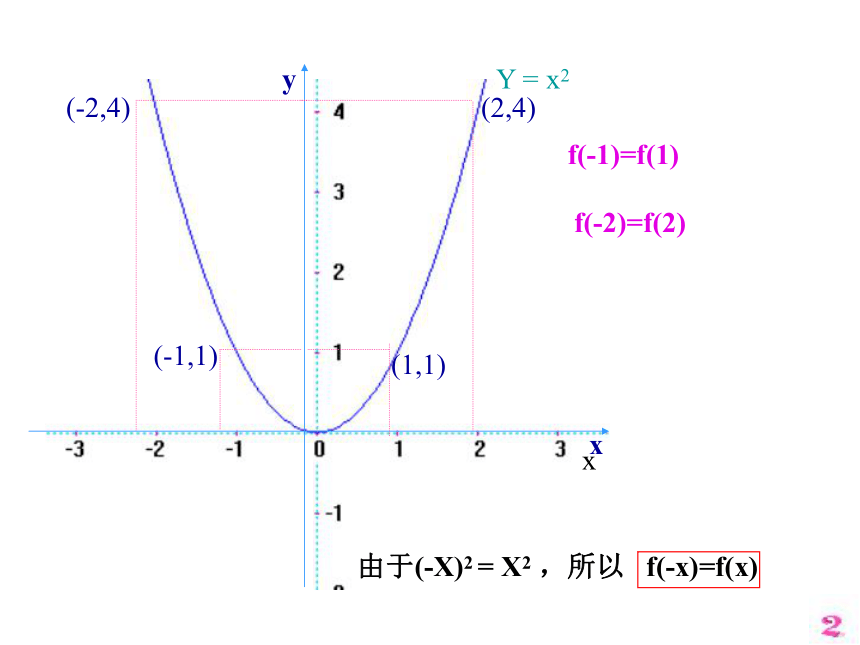
3 奇函数,偶函数的图像各有什么样的对称性质?Y = x2xxy(2,4)(-2,4)f(-2)=f(2)由于(-X)2 = X2 ,所以 f(-x)=f(x)f(-1)=f(1)(1,1)(-1,1)函 数 的 奇 偶 性正式上课f(-2)=f(2)由于|-X| =| X| ,所以 f(-x)=f(x)1.偶函数 一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=f(x),那么f(x)就叫做偶函数
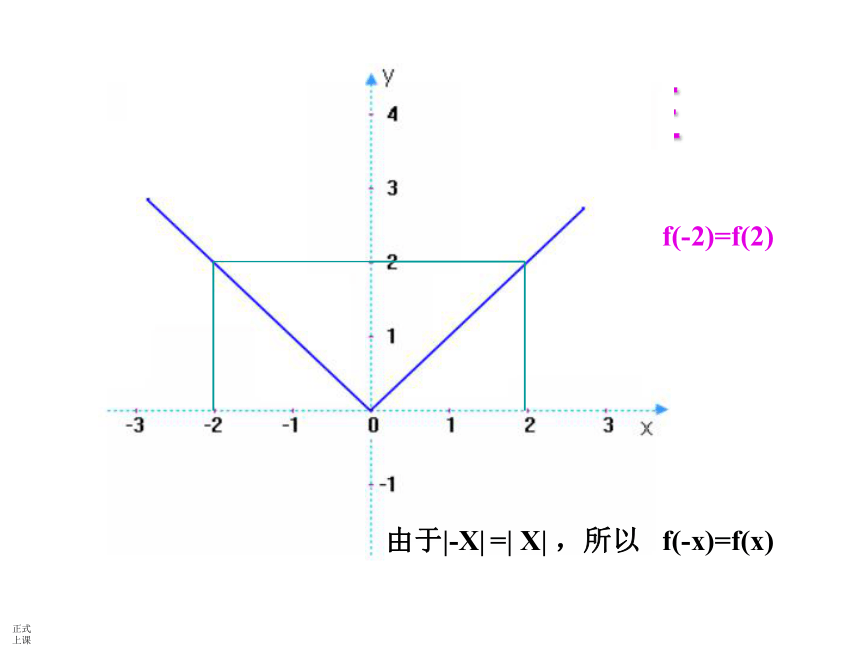
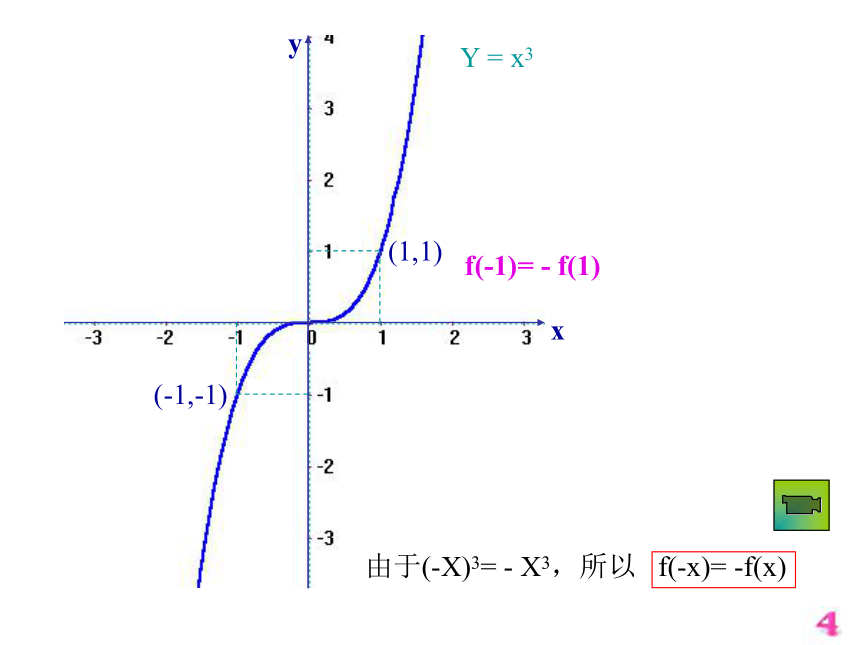
偶函数的图像关轴对称. Y = x3xy(1,1)(-1,-1)f(-1)= - f(1)由于(-X)3= - X3,所以 f(-x)= -f(x)2.奇函数 一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)= -f(x),那么f(x)就叫做奇函数.奇函数的图像关于原点对称. 注意:
1由函数的奇偶性定义可知,函数具有奇偶性的一个必要条件是,对于定义域内的任意一个x,则-x也一定是定义域内的一个自变量(即定义域关于原点对称).
2奇、偶函数定义的逆命题也成立,即
若f(x)为奇函数,则f(-x)=-f(x)有成立.
若f(x)为偶函数,则f(-x)=f(x)有成立.
3函数是奇函数或是偶函数称为函数的奇偶性,函数的奇偶性是函数的整体性质;
4如果一个函数f(x)是奇函数或偶函数,那么我们就说函数f(x)具有奇偶性.3.奇偶函数图象的性质1、奇函数的图象关于原点对称. 反过来,如果一个函数的图象关于原点对称,那么就称这个函数为奇函数.2、偶函数的图象关于y轴对称. 反过来,如果一个函数的图象关于y轴对称,那么就称这个函数为偶函数.说明:奇偶函数图象的性质可用于:
a、简化函数图象的画法. b、判断函数的奇偶性例3、已知函数y=f(x)是偶函数,它在y轴右边的图象如下图,画出在y轴左边的图象.解:画法略本课小结1、两个定义:对于f(x)定义域内的任意一个x,
如果都有f(-x)=-f(x) f(x)为奇函数
如果都有f(-x)=f(x) f(x)为偶函数2、两个性质:
一个函数为奇函数 它的图象关于原点对称
一个函数为偶函数 它的图象关于y轴对称例1:判断下列函数的奇偶性:(1)解:定义域为R ∵ f(-x)=(-x)4=f(x)即f(-x)=f(x)∴f(x)偶函数(2)解:定义域为R f(-x)=(-x)5=- x5 =-f(x)即f(-x)=-f(x)∴f(x)奇函数(3)解:定义域为{x|x≠0} ∵ f(-x)=-x+1/(-x)=-f(x)即f(-x)=-f(x)∴f(x)奇函数(4)解:定义域为{x|x≠0} ∵ f(-x)=1/(-x)2=f(x)即f(-x)=f(x)∴f(x)偶函数课堂练习1判断下列函数的奇偶性:课堂练习2 小结
1用定义判断函数奇偶性的步骤:
①先求定义域,看是否关于原点称;②再判断f(-x)=-f(x)或f(-x)=f(x)是否恒成立.课堂练习3若f(x)是定义在R上的奇函数,当x<0时,
f(x)=x(1-x),求当x 0时函数的解析式
解:当x>0时,-x<0,因当x<0时f(x)=x(1-x),
则f(-x)=-x(1+x).又f(x)为奇函数有f(-x)=- f(x), 所以-f(x)=-x(1+x),则f(x)=x(1+x),
又f(0)=f(-0)=-f(0),则f(0)=0
则当x 0 时,f(x)=x(1+x)课堂练习4课堂练习5
2 什么是偶函数?
3 奇函数,偶函数的图像各有什么样的对称性质?Y = x2xxy(2,4)(-2,4)f(-2)=f(2)由于(-X)2 = X2 ,所以 f(-x)=f(x)f(-1)=f(1)(1,1)(-1,1)函 数 的 奇 偶 性正式上课f(-2)=f(2)由于|-X| =| X| ,所以 f(-x)=f(x)1.偶函数 一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=f(x),那么f(x)就叫做偶函数
偶函数的图像关轴对称. Y = x3xy(1,1)(-1,-1)f(-1)= - f(1)由于(-X)3= - X3,所以 f(-x)= -f(x)2.奇函数 一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)= -f(x),那么f(x)就叫做奇函数.奇函数的图像关于原点对称. 注意:
1由函数的奇偶性定义可知,函数具有奇偶性的一个必要条件是,对于定义域内的任意一个x,则-x也一定是定义域内的一个自变量(即定义域关于原点对称).
2奇、偶函数定义的逆命题也成立,即
若f(x)为奇函数,则f(-x)=-f(x)有成立.
若f(x)为偶函数,则f(-x)=f(x)有成立.
3函数是奇函数或是偶函数称为函数的奇偶性,函数的奇偶性是函数的整体性质;
4如果一个函数f(x)是奇函数或偶函数,那么我们就说函数f(x)具有奇偶性.3.奇偶函数图象的性质1、奇函数的图象关于原点对称. 反过来,如果一个函数的图象关于原点对称,那么就称这个函数为奇函数.2、偶函数的图象关于y轴对称. 反过来,如果一个函数的图象关于y轴对称,那么就称这个函数为偶函数.说明:奇偶函数图象的性质可用于:
a、简化函数图象的画法. b、判断函数的奇偶性例3、已知函数y=f(x)是偶函数,它在y轴右边的图象如下图,画出在y轴左边的图象.解:画法略本课小结1、两个定义:对于f(x)定义域内的任意一个x,
如果都有f(-x)=-f(x) f(x)为奇函数
如果都有f(-x)=f(x) f(x)为偶函数2、两个性质:
一个函数为奇函数 它的图象关于原点对称
一个函数为偶函数 它的图象关于y轴对称例1:判断下列函数的奇偶性:(1)解:定义域为R ∵ f(-x)=(-x)4=f(x)即f(-x)=f(x)∴f(x)偶函数(2)解:定义域为R f(-x)=(-x)5=- x5 =-f(x)即f(-x)=-f(x)∴f(x)奇函数(3)解:定义域为{x|x≠0} ∵ f(-x)=-x+1/(-x)=-f(x)即f(-x)=-f(x)∴f(x)奇函数(4)解:定义域为{x|x≠0} ∵ f(-x)=1/(-x)2=f(x)即f(-x)=f(x)∴f(x)偶函数课堂练习1判断下列函数的奇偶性:课堂练习2 小结
1用定义判断函数奇偶性的步骤:
①先求定义域,看是否关于原点称;②再判断f(-x)=-f(x)或f(-x)=f(x)是否恒成立.课堂练习3若f(x)是定义在R上的奇函数,当x<0时,
f(x)=x(1-x),求当x 0时函数的解析式
解:当x>0时,-x<0,因当x<0时f(x)=x(1-x),
则f(-x)=-x(1+x).又f(x)为奇函数有f(-x)=- f(x), 所以-f(x)=-x(1+x),则f(x)=x(1+x),
又f(0)=f(-0)=-f(0),则f(0)=0
则当x 0 时,f(x)=x(1+x)课堂练习4课堂练习5
