16.1.1--16.1.2 分式的复习
文档属性
| 名称 | 16.1.1--16.1.2 分式的复习 |

|
|
| 格式 | rar | ||
| 文件大小 | 755.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-02-24 06:52:00 | ||
图片预览







文档简介
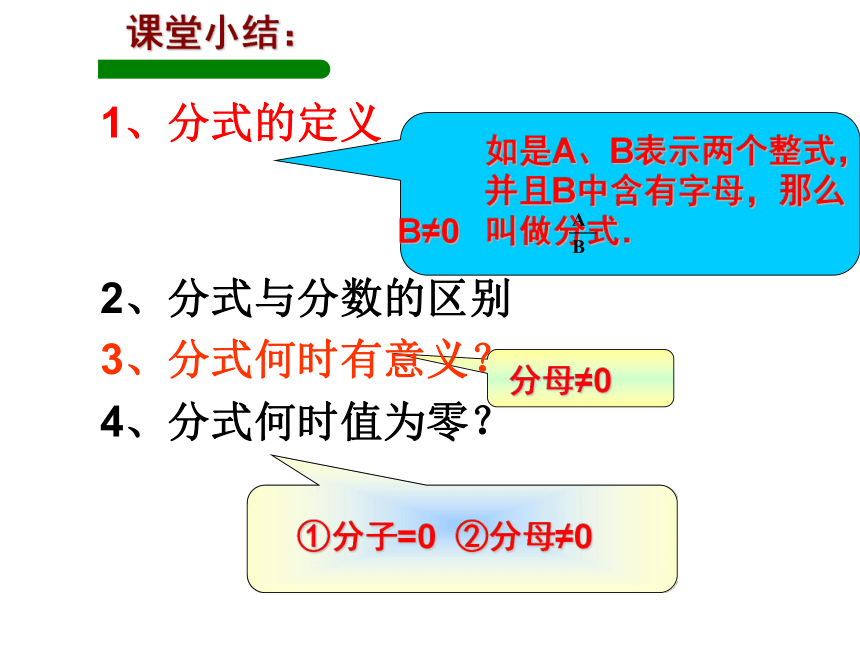
课件25张PPT。南门学校八年(3)(5)班16.1.1--16.1.2 分式的复习想一想下列各式中,哪些是整式?哪些是分式?整式与分式的区别:整式的分母中不含字母,而分式的分母中含有字母.整式和分式统称为有理式.整式分式有理式分母≠0 ①分子=0 ②分母≠0如是A、B表示两个整式,并且B中含有字母,那么 叫做分式.1、分式的定义2、分式与分数的区别3、分式何时有意义?4、分式何时值为零?B≠0例2、当 x 取什么值时,下列分式的值为零 :补充例题解⑴:由分子x+2=0,得 x=-2。而当 x=-2时,分母 2x-5=-4-5≠0。(1)(2)所以当x=-2时,分式 的值是零。解⑵ :由分子|x|-2=0,得 x=±2。当x=2时,分母 2x+4=4+4≠0。当x=-2时,分母 2x+4=-4+4=0。所以当x=2时,分式 的值是零。分式有意义的条件:
分式的分母不等于零分式的值为零的条件:
分式的分子等于零且分母不等于零分式无意义的条件:归纳
分式的分母等于零
分式的值为正或负的条件:
同号得正,异号得负5.下列分式,当x取何值时有意义. 6.下列各式中,无论x取何值,分式
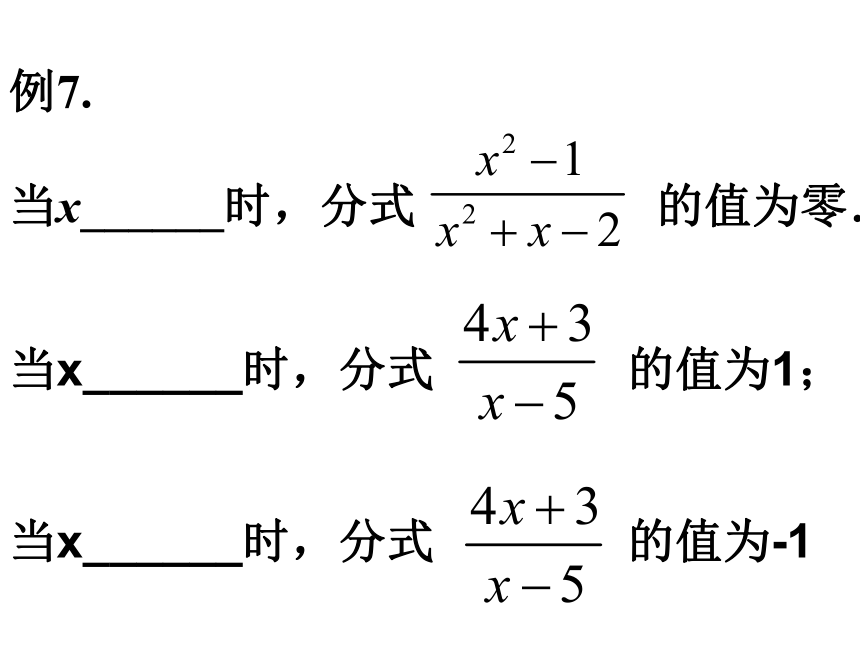
都有意义的是( ) 例7.
当x______时,分式 的值为零. 当x______时,分式 的值为1;
当x______时,分式 的值为-1 练习1.当x为何值时,下列分式有意义?2.当x为何值时,下列分式的值为0? 1、 若m、n都是小于5的整数,且 ,
则m、n的值分别是( )A. m=4;n=3B. m=3;n=2C. m=1;n=1D. m=2;n=3 2、要使分式有意义,只需要( ) A .x ≠1B. x ≠ 3C. x≠-1且x≠3D. x≠-1 或 x≠3B要求m>n且n为偶数.Cx=3时分母为零x=-1时分母为零只取一个不行分式的基本性质 分式的分子与分母同乘(或除以)一个不等于0的整式,分式的值不变。用式子表示为:其中A,B,C是整式。: 把分子.分母的最大公因式(数)约去.
关键是找最简公分母:1.约分2.通分:: 把分母不相同的几个分式化成分母相同的分式.约分的基本步骤:(1)若分子﹑分母都是单项式,则约简系数,并约去相同字母的最低次幂;
(2)若分子﹑分母含有多项式,则先将多项式
分解因式,然后约去分子﹑分母所有的公因式.最简公分母系数的最小公倍数相同因式的最高次幂的积单独的字母放进去化简分式时,通常要使结果化成最简分式或整式2y3x2-3xy4n2ab+1 不改变分式的值,使下列分式的分子与分母都不含“-”号解:2。练习:3。不改变分式的值将下列各式中的系数都化成整数.三、例题讲解与练习例4.不改变分式的值,使下列各式的分子与分母中的多项
式按 的降幂排列,且首项的系数是正数.解:5。通分:6。约分:约分:通分:1、下列约分正确的个数有 ( )A、1个 B、2个 C、3个 D、0个 B练习2、下列各式中是最简分式的( )B练习小 医生诊断下列分式的变形是否有“病”-练习思考题(2)已知 abc=1, 求证:1、约分:2、最简分式:3、化简分式时,通常使结果成为最简分式或整式。把一个分式的分子和分母的公因式
约去,这种变形叫做分式的约分分子和分母已没有公因式,这样的
分式成为最简分式4.把各分式化成相同分母的分式叫做分式的通分.小 结再见
分式的分母不等于零分式的值为零的条件:
分式的分子等于零且分母不等于零分式无意义的条件:归纳
分式的分母等于零
分式的值为正或负的条件:
同号得正,异号得负5.下列分式,当x取何值时有意义. 6.下列各式中,无论x取何值,分式
都有意义的是( ) 例7.
当x______时,分式 的值为零. 当x______时,分式 的值为1;
当x______时,分式 的值为-1 练习1.当x为何值时,下列分式有意义?2.当x为何值时,下列分式的值为0? 1、 若m、n都是小于5的整数,且 ,
则m、n的值分别是( )A. m=4;n=3B. m=3;n=2C. m=1;n=1D. m=2;n=3 2、要使分式有意义,只需要( ) A .x ≠1B. x ≠ 3C. x≠-1且x≠3D. x≠-1 或 x≠3B要求m>n且n为偶数.Cx=3时分母为零x=-1时分母为零只取一个不行分式的基本性质 分式的分子与分母同乘(或除以)一个不等于0的整式,分式的值不变。用式子表示为:其中A,B,C是整式。: 把分子.分母的最大公因式(数)约去.
关键是找最简公分母:1.约分2.通分:: 把分母不相同的几个分式化成分母相同的分式.约分的基本步骤:(1)若分子﹑分母都是单项式,则约简系数,并约去相同字母的最低次幂;
(2)若分子﹑分母含有多项式,则先将多项式
分解因式,然后约去分子﹑分母所有的公因式.最简公分母系数的最小公倍数相同因式的最高次幂的积单独的字母放进去化简分式时,通常要使结果化成最简分式或整式2y3x2-3xy4n2ab+1 不改变分式的值,使下列分式的分子与分母都不含“-”号解:2。练习:3。不改变分式的值将下列各式中的系数都化成整数.三、例题讲解与练习例4.不改变分式的值,使下列各式的分子与分母中的多项
式按 的降幂排列,且首项的系数是正数.解:5。通分:6。约分:约分:通分:1、下列约分正确的个数有 ( )A、1个 B、2个 C、3个 D、0个 B练习2、下列各式中是最简分式的( )B练习小 医生诊断下列分式的变形是否有“病”-练习思考题(2)已知 abc=1, 求证:1、约分:2、最简分式:3、化简分式时,通常使结果成为最简分式或整式。把一个分式的分子和分母的公因式
约去,这种变形叫做分式的约分分子和分母已没有公因式,这样的
分式成为最简分式4.把各分式化成相同分母的分式叫做分式的通分.小 结再见
