对数函数及其性质
图片预览






文档简介
课件22张PPT。对数函数及其性质第一课时 对数函数的概念与图象2.2.2 本节课的学习预告:1.对数函数的定义
2.画出对数函数的图象
3.对数函数性质与应用考古学家一般通过提取附着在出土文物、古遗址上死亡的残留物,利用
估计出土文物或古遗址的年代。 t 能不能看成是 P 的函数? 根据问题的实际意义可知,对于每一个碳14含量P,通过对应关系 ,都有唯
一确定的年代 t 与它对应,所以,t 是P的函数。 一般地,函数y = loga x (a>0,且a≠ 1)叫做对数函数.其中 x是自变量, 函数的定义域是( 0 , +∞)求下列函数的定义域:巩固练习(1):P73方框练习T2(1){x|x≠0}(2){x|x<4} (3){x|x>1} (4){x|x>0且x≠1}我试试我理解在同一坐标系中用描点法画出对数函数
的图象。作图步骤: ①列表,
②描点,
③连线。对数函数:y = loga x (a>0,且a≠ 1)
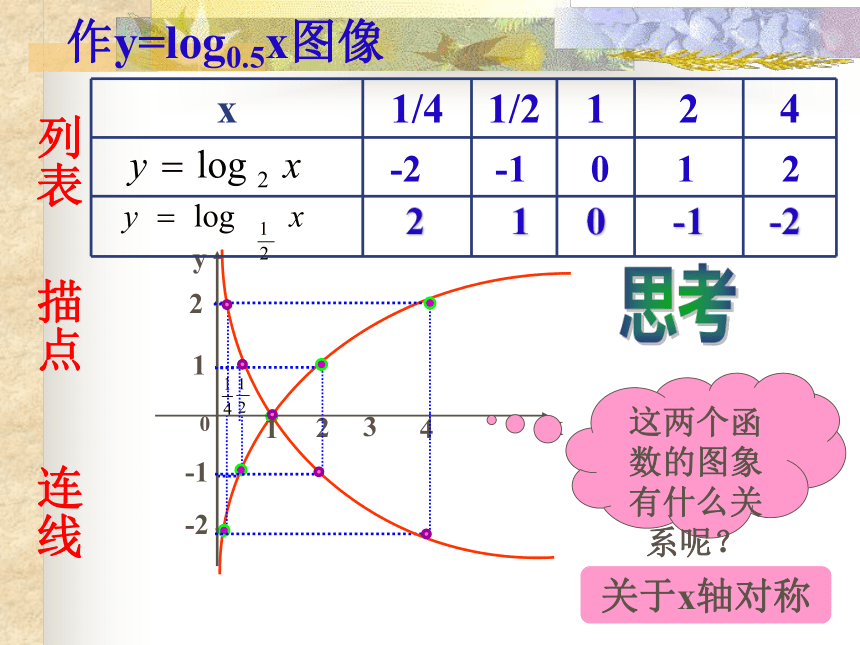
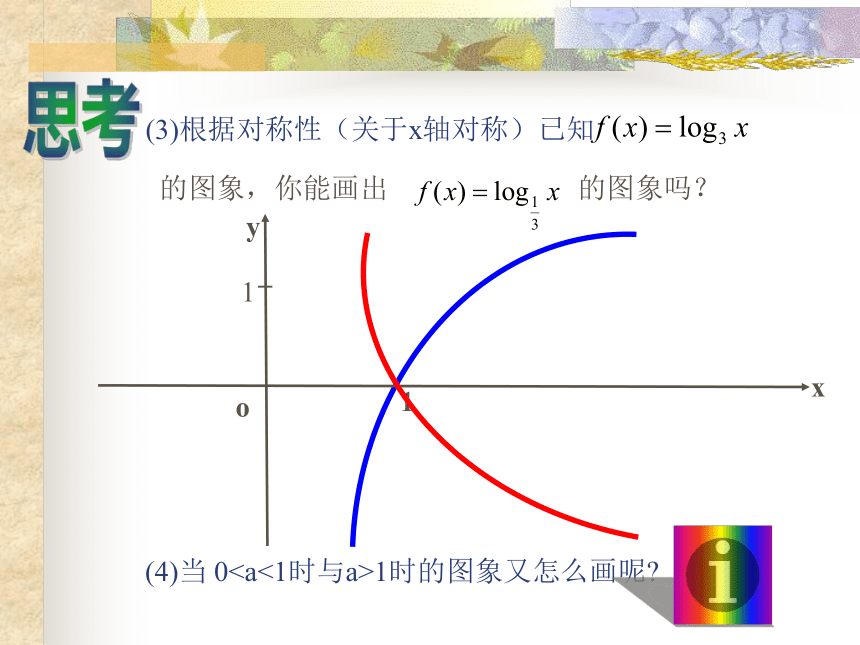
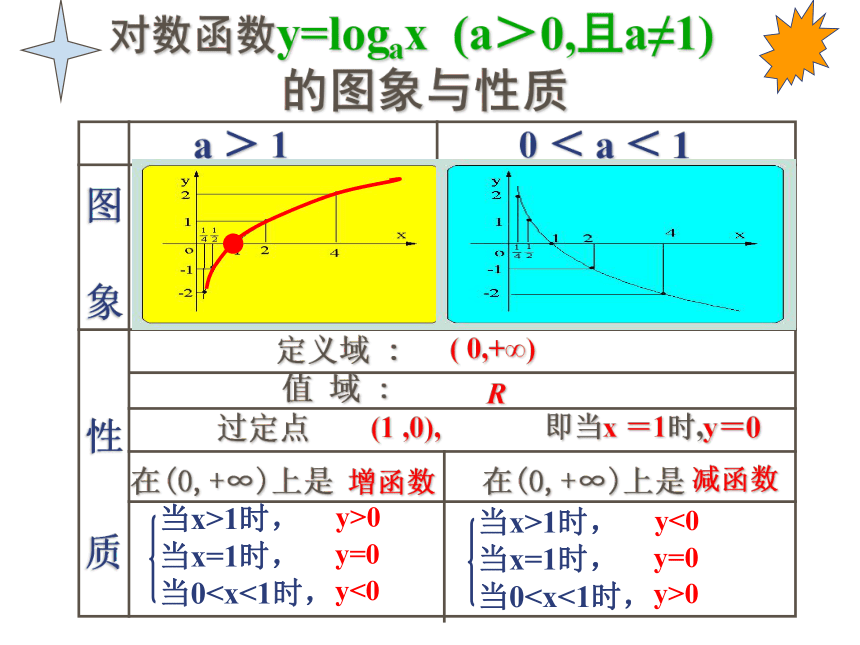
图象与性质列表描点作y=log2x图象连线列表描点作y=log0.5x图像连线 2 1 0 -1 -2 -2 -1 0 1 2 思考这两个函数的图象有什么关系呢?关于x轴对称(3)根据对称性(关于x轴对称)已知思考(4)当 01时的图象又怎么画呢?jihehuaban图 象 性 质a > 1 0 < a < 1定义域 : 值 域 :过定点在(0,+∞)上是在(0,+∞)上是( 0,+∞)R
(1 ,0), 即当x =1时,y=0增函数减函数y>0y=0y<0 y<0y=0y>0 下列是6个对数函数的图象,比较它们底
数的大小 规律:在 x=1的右边
看图象,图象越高底数越小.即图高底小我试试我理解 底数a>1时,底数越大,其图象越接近x轴。补充性质二 底数互为倒数的两个对数函数的图象关于x轴对称。补充性质一
图
形1 底数0(1) log23.4与 log28.5 (2) log 0.3 1.8与 log 0.3 2.7 log23.4log28.5∴ log23.4< log28.5解法1:画图找点比高低解法2:利用对数函数的单调性考察函数y=log 2 x ,∵a=2 > 1,∴函数在区间(0,+∞)
上是增函数;∵3.4<8.5∴ log23.4< log28.5我练练我掌握 比较下列各组中,两个值的大小:
(1) log23.4与 log28.5 (2) log 0.3 1.8与 log 0.3 2.7解法2:考察函数y=log 0.3 x ,
∵a=0.3< 1,
∴函数在区间(0,+∞)上是减函数;
∵1.8<2.7
∴ log 0.3 1.8> log 0.3 2.7 (2)解法1:画图找点比高低我练练我掌握小结 比较下列各组中,两个值的大小:
(1) log23.4与 log28.5 (2) log 0.3 1.8与 log 0.3 2.7小
结比较两个同底对数值的大小时:1.观察底数是大于1还是小于1( a>1时为增函数
0即0 1 比较下列各组中,两个值的大小:
(3) loga5.1与 loga5.9解: ①若a>1则函数在区间(0,+∞)上是增函数;
∵5.1<5.9
∴ loga5.1 < loga5.9
②若0 ∴ loga5.1 > loga5.9我练练我掌握你能口答吗?变一变还能口答吗?<>><<<<< 比较下列各组中两个值的大小:
⑴ log 67 , log 7 6 ; ⑵ log 3π , log 2 0.8 . 解: ⑴∵log67>log66=1
log76<log77=1
∴ log67>log76 ⑵ ∵log3π>log31=0
log20.8<log21=0
∴ log3π>log20.8 注意:利用对数函数的增减性比较两个对数的大小.当不能直接进行比较时,可在两个对数中间插入一个已知数(如1或0等),间接比较上述两个对数的大小提示 : log aa=1提示: log a1=0小技巧:判断对数 与0的大小是
只要比较(a-1)(b-1)与0的大小我分析我发展 比较下列各组中两个值的大小:
⑴ log 67 , log 7 6 ; ⑵ log 3π , log 2 0.8 . 注意:利用对数函数的增减性比较两个对数的大小.当不能直接进行比较时,可在两个对数中间插入一个已知数(如1或0等),间接比较上述两个对数的大小提示 : log aa=1提示: log a1=0小技巧:判断对数 与0的大小是
只要比较(a-1)(b-1)与0的大小我分析我发展(3)巩固练习:P73 T3小 结二、对数函数的图象和性质;三、比较两个对数值的大小.一、对数函数的定义;图 象 性 质a > 1 0 < a < 1定义域 : ( 0,+∞) 值 域 : R过点(1 ,0), 即当x =1时,y=0在(0,+∞)上是增函数 在(0,+∞)上是减函数㈠ 若底数为同一常数,则可由对数函数的单调性直接进行判断.
㈡ 若底数为同一字母,则按对数函数的单调性对底数进行分类讨论.
㈢ 若底数、真数都不相同,则常借助1、0、-1等中间量进行比较 比较两个对数值的大小.(1)作业 Ⅰ 熟记对数函数
的图象和性质
Ⅱ P74.习题2.2 7,8
2.画出对数函数的图象
3.对数函数性质与应用考古学家一般通过提取附着在出土文物、古遗址上死亡的残留物,利用
估计出土文物或古遗址的年代。 t 能不能看成是 P 的函数? 根据问题的实际意义可知,对于每一个碳14含量P,通过对应关系 ,都有唯
一确定的年代 t 与它对应,所以,t 是P的函数。 一般地,函数y = loga x (a>0,且a≠ 1)叫做对数函数.其中 x是自变量, 函数的定义域是( 0 , +∞)求下列函数的定义域:巩固练习(1):P73方框练习T2(1){x|x≠0}(2){x|x<4} (3){x|x>1} (4){x|x>0且x≠1}我试试我理解在同一坐标系中用描点法画出对数函数
的图象。作图步骤: ①列表,
②描点,
③连线。对数函数:y = loga x (a>0,且a≠ 1)
图象与性质列表描点作y=log2x图象连线列表描点作y=log0.5x图像连线 2 1 0 -1 -2 -2 -1 0 1 2 思考这两个函数的图象有什么关系呢?关于x轴对称(3)根据对称性(关于x轴对称)已知思考(4)当 0
(1 ,0), 即当x =1时,y=0增函数减函数y>0y=0y<0 y<0y=0y>0 下列是6个对数函数的图象,比较它们底
数的大小 规律:在 x=1的右边
看图象,图象越高底数越小.即图高底小我试试我理解 底数a>1时,底数越大,其图象越接近x轴。补充性质二 底数互为倒数的两个对数函数的图象关于x轴对称。补充性质一
图
形1 底数0
上是增函数;∵3.4<8.5∴ log23.4< log28.5我练练我掌握 比较下列各组中,两个值的大小:
(1) log23.4与 log28.5 (2) log 0.3 1.8与 log 0.3 2.7解法2:考察函数y=log 0.3 x ,
∵a=0.3< 1,
∴函数在区间(0,+∞)上是减函数;
∵1.8<2.7
∴ log 0.3 1.8> log 0.3 2.7 (2)解法1:画图找点比高低我练练我掌握小结 比较下列各组中,两个值的大小:
(1) log23.4与 log28.5 (2) log 0.3 1.8与 log 0.3 2.7小
结比较两个同底对数值的大小时:1.观察底数是大于1还是小于1( a>1时为增函数
0
(3) loga5.1与 loga5.9解: ①若a>1则函数在区间(0,+∞)上是增函数;
∵5.1<5.9
∴ loga5.1 < loga5.9
②若0
⑴ log 67 , log 7 6 ; ⑵ log 3π , log 2 0.8 . 解: ⑴∵log67>log66=1
log76<log77=1
∴ log67>log76 ⑵ ∵log3π>log31=0
log20.8<log21=0
∴ log3π>log20.8 注意:利用对数函数的增减性比较两个对数的大小.当不能直接进行比较时,可在两个对数中间插入一个已知数(如1或0等),间接比较上述两个对数的大小提示 : log aa=1提示: log a1=0小技巧:判断对数 与0的大小是
只要比较(a-1)(b-1)与0的大小我分析我发展 比较下列各组中两个值的大小:
⑴ log 67 , log 7 6 ; ⑵ log 3π , log 2 0.8 . 注意:利用对数函数的增减性比较两个对数的大小.当不能直接进行比较时,可在两个对数中间插入一个已知数(如1或0等),间接比较上述两个对数的大小提示 : log aa=1提示: log a1=0小技巧:判断对数 与0的大小是
只要比较(a-1)(b-1)与0的大小我分析我发展(3)巩固练习:P73 T3小 结二、对数函数的图象和性质;三、比较两个对数值的大小.一、对数函数的定义;图 象 性 质a > 1 0 < a < 1定义域 : ( 0,+∞) 值 域 : R过点(1 ,0), 即当x =1时,y=0在(0,+∞)上是增函数 在(0,+∞)上是减函数㈠ 若底数为同一常数,则可由对数函数的单调性直接进行判断.
㈡ 若底数为同一字母,则按对数函数的单调性对底数进行分类讨论.
㈢ 若底数、真数都不相同,则常借助1、0、-1等中间量进行比较 比较两个对数值的大小.(1)作业 Ⅰ 熟记对数函数
的图象和性质
Ⅱ P74.习题2.2 7,8
