27.2.1相似三角形的判定
文档属性
| 名称 | 27.2.1相似三角形的判定 |  | |
| 格式 | rar | ||
| 文件大小 | 948.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-02-26 10:50:00 | ||
图片预览


文档简介
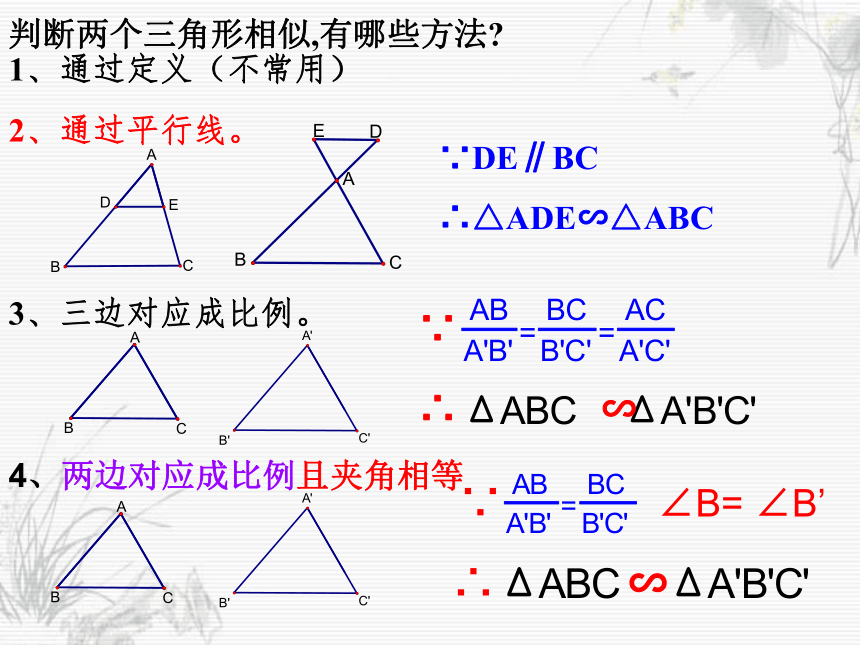
课件16张PPT。27.2.1 相似三角形的判定判断两个三角形相似,有哪些方法?1、通过定义(不常用)2、通过平行线。3、三边对应成比例。∵DE∥BC
∴△ADE∽△ABC4、两边对应成比例且夹角相等∵ ∠B= ∠B’∴ ∽观察两副三角尺,其中同样角度(300与600,或450与450)的两个三角尺相似吗?. 一般地,如果两个三角形有两个对应角相等,它们一定相似吗?
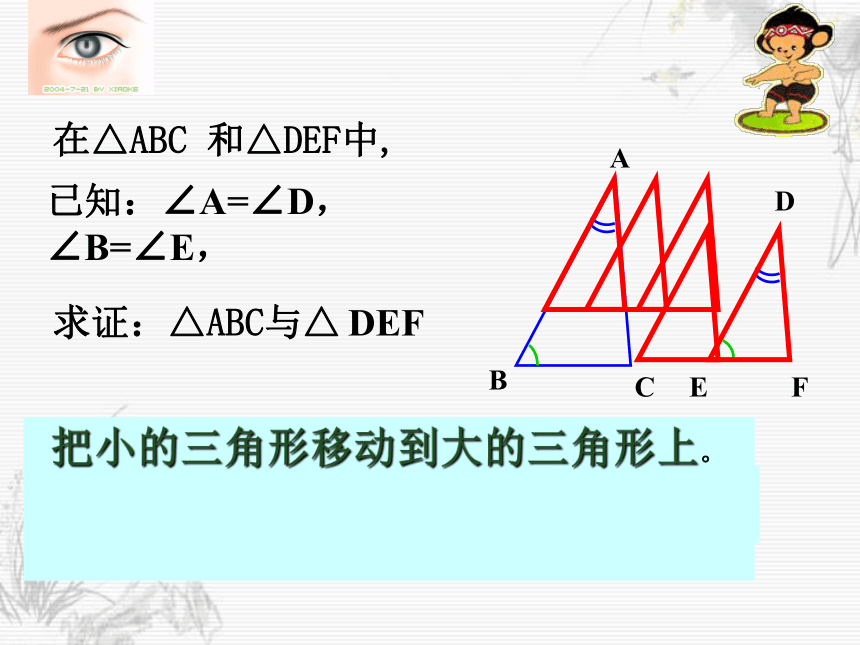
怎样创造相似的条件?在△ABC 和△DEF中,求证:△ABC与△ DEF已知:∠A=∠D,∠B=∠E,把小的三角形移动到大的三角形上。
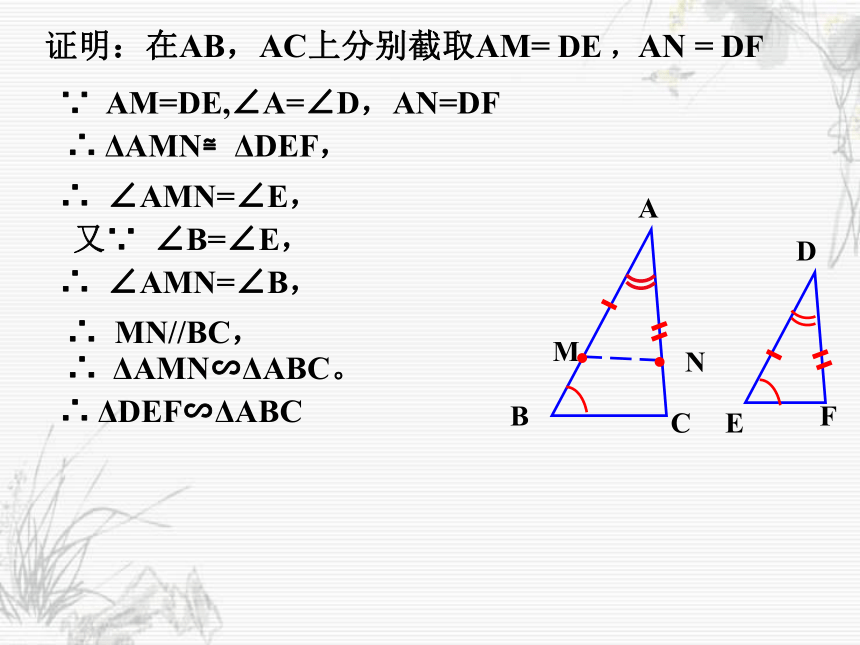
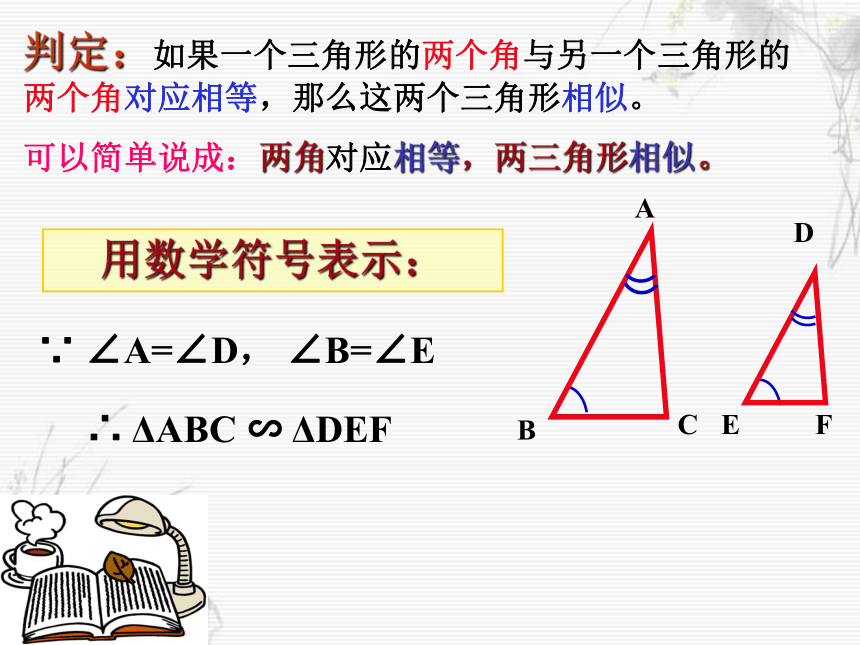
ABCD F E ∵ AM=DE,∠A=∠D,AN=DF∴ ΔAMN≌ΔDEF,∴ ∠AMN=∠E,又∵ ∠B=∠E,∴ ∠AMN=∠B,∴ MN//BC,∴ ΔAMN∽ΔABC。∴ ΔDEF∽ΔABC证明:在AB,AC上分别截取AM= DE ,AN = DFCF∵ ∠A=∠D, ∠B=∠E∴ ΔABC ∽ ΔDEF用数学符号表示:判定:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
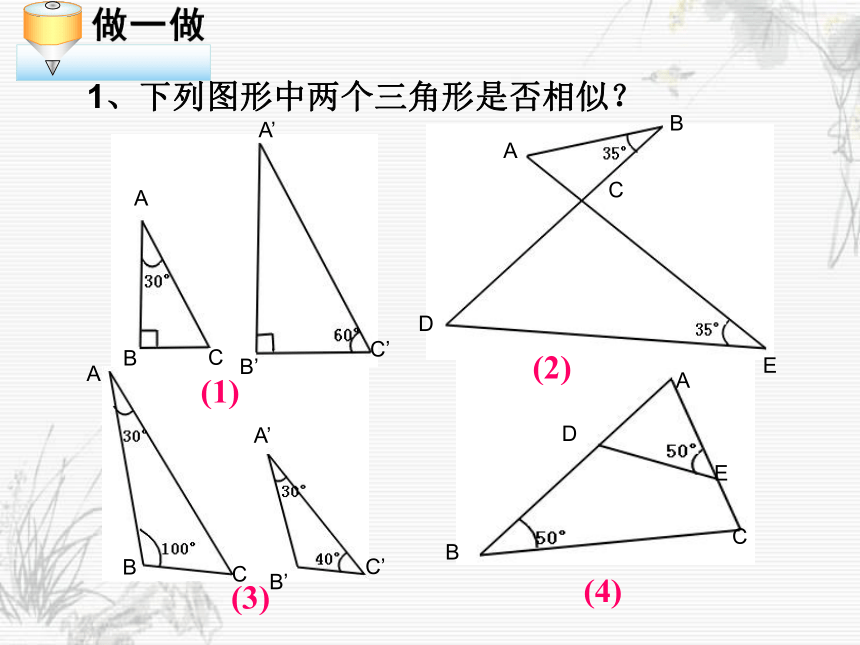
可以简单说成:两角对应相等,两三角形相似。1、下列图形中两个三角形是否相似?(1)(2)(3)(4)2、判断题:
⑴所有的直角三角形都相似 . ( )
⑵有一个锐角对应相等的两直角三角形相似.( )
⑶所有的等边三角形都相似. ( )
⑷所有的等腰直角三角形都相似. ( )
⑸顶角相等的两个等腰三角形相似. ( )
⑹有一个角相等的两个等腰三角形相似. ( )
×√√ √√×例、 如图,弦AB和CD相交于⊙O内一点P,
求证PA·PB=PC·PD.证明:连结AC﹑BD.∵∠A和∠B都是BC所对的圆周角.
∴∠A=∠D.
同理 ∠C=∠B.
∴△PAC∽△PDB,∴PA:PD=PC:PB
即:PA·PB=PC·PD.1、已知D、E分别是△ABC的边AB,AC上的点,若∠A=35°, ∠C=85°,∠AED=60 °
求证:AD·AB= AE·AC2、乐业大石围天坑是百色市有名的旅游景点,为了测量一个峡谷的宽度,地质勘探人员在对面的岩石上观察到一个特别明显的标点O,再在他们所在的这一侧选点A、B、D,使得AB⊥AO, DB⊥AB,然后确定DO和AB的交点C,测得AC=60米,CB=30米,BD=12米,你能帮助他们算出峡谷的宽AO吗?3. 如图,△ABC中,
DE∥BC,EF∥AB,
试说明△ADE∽△EFC. 解: ∵ DE∥BC,EF∥AB∴ ∠ADE=∠B=∠EFC∠AED=∠C. ∴ △ADE∽△EFC. 拓展
(1)如图3,点D在AB上,当∠ =∠ 时,
△ACD∽△ABC。
(2)如图4,已知点E在AC上,若点D在AB上,则满足
条件 ,就可以使△ADE与原△ABC相似。
∠ ACD∠ B (或者∠ ACB=∠ ADB)DE//BC(或者∠ C=∠ ADE)DD拓展
(1)如图3,点D在AB上,当∠ =∠ 时,
△ACD∽△ABC。
(2)如图4,已知点E在AC上,若点D在AB上,则满足
条件 ,就可以使△ADE与原△ABC相似。
∠ ACD∠ B (或者∠ ACB=∠ ADB)DE//BC(或者∠ C=∠ ADE)(或者∠ B=∠ ADE)相似三角形的识别方法有那些?方法1:通过定义方法5:通过两角对应相等。课 堂 小 结(这可是今天新学的,要牢记噢!)方法2:平行于三角形一边的直线。方法3:三边对应成比例。方法4:两边对应成比例且夹角相等。
∴△ADE∽△ABC4、两边对应成比例且夹角相等∵ ∠B= ∠B’∴ ∽观察两副三角尺,其中同样角度(300与600,或450与450)的两个三角尺相似吗?. 一般地,如果两个三角形有两个对应角相等,它们一定相似吗?
怎样创造相似的条件?在△ABC 和△DEF中,求证:△ABC与△ DEF已知:∠A=∠D,∠B=∠E,把小的三角形移动到大的三角形上。
ABCD F E ∵ AM=DE,∠A=∠D,AN=DF∴ ΔAMN≌ΔDEF,∴ ∠AMN=∠E,又∵ ∠B=∠E,∴ ∠AMN=∠B,∴ MN//BC,∴ ΔAMN∽ΔABC。∴ ΔDEF∽ΔABC证明:在AB,AC上分别截取AM= DE ,AN = DFCF∵ ∠A=∠D, ∠B=∠E∴ ΔABC ∽ ΔDEF用数学符号表示:判定:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
可以简单说成:两角对应相等,两三角形相似。1、下列图形中两个三角形是否相似?(1)(2)(3)(4)2、判断题:
⑴所有的直角三角形都相似 . ( )
⑵有一个锐角对应相等的两直角三角形相似.( )
⑶所有的等边三角形都相似. ( )
⑷所有的等腰直角三角形都相似. ( )
⑸顶角相等的两个等腰三角形相似. ( )
⑹有一个角相等的两个等腰三角形相似. ( )
×√√ √√×例、 如图,弦AB和CD相交于⊙O内一点P,
求证PA·PB=PC·PD.证明:连结AC﹑BD.∵∠A和∠B都是BC所对的圆周角.
∴∠A=∠D.
同理 ∠C=∠B.
∴△PAC∽△PDB,∴PA:PD=PC:PB
即:PA·PB=PC·PD.1、已知D、E分别是△ABC的边AB,AC上的点,若∠A=35°, ∠C=85°,∠AED=60 °
求证:AD·AB= AE·AC2、乐业大石围天坑是百色市有名的旅游景点,为了测量一个峡谷的宽度,地质勘探人员在对面的岩石上观察到一个特别明显的标点O,再在他们所在的这一侧选点A、B、D,使得AB⊥AO, DB⊥AB,然后确定DO和AB的交点C,测得AC=60米,CB=30米,BD=12米,你能帮助他们算出峡谷的宽AO吗?3. 如图,△ABC中,
DE∥BC,EF∥AB,
试说明△ADE∽△EFC. 解: ∵ DE∥BC,EF∥AB∴ ∠ADE=∠B=∠EFC∠AED=∠C. ∴ △ADE∽△EFC. 拓展
(1)如图3,点D在AB上,当∠ =∠ 时,
△ACD∽△ABC。
(2)如图4,已知点E在AC上,若点D在AB上,则满足
条件 ,就可以使△ADE与原△ABC相似。
∠ ACD∠ B (或者∠ ACB=∠ ADB)DE//BC(或者∠ C=∠ ADE)DD拓展
(1)如图3,点D在AB上,当∠ =∠ 时,
△ACD∽△ABC。
(2)如图4,已知点E在AC上,若点D在AB上,则满足
条件 ,就可以使△ADE与原△ABC相似。
∠ ACD∠ B (或者∠ ACB=∠ ADB)DE//BC(或者∠ C=∠ ADE)(或者∠ B=∠ ADE)相似三角形的识别方法有那些?方法1:通过定义方法5:通过两角对应相等。课 堂 小 结(这可是今天新学的,要牢记噢!)方法2:平行于三角形一边的直线。方法3:三边对应成比例。方法4:两边对应成比例且夹角相等。
