5.2.1平行线
图片预览











文档简介
课件34张PPT。你喜欢滑雪吗?早在5000年前,人们就把滑雪作为雪上旅行的一种方式。滑雪运动最关键的是要保持
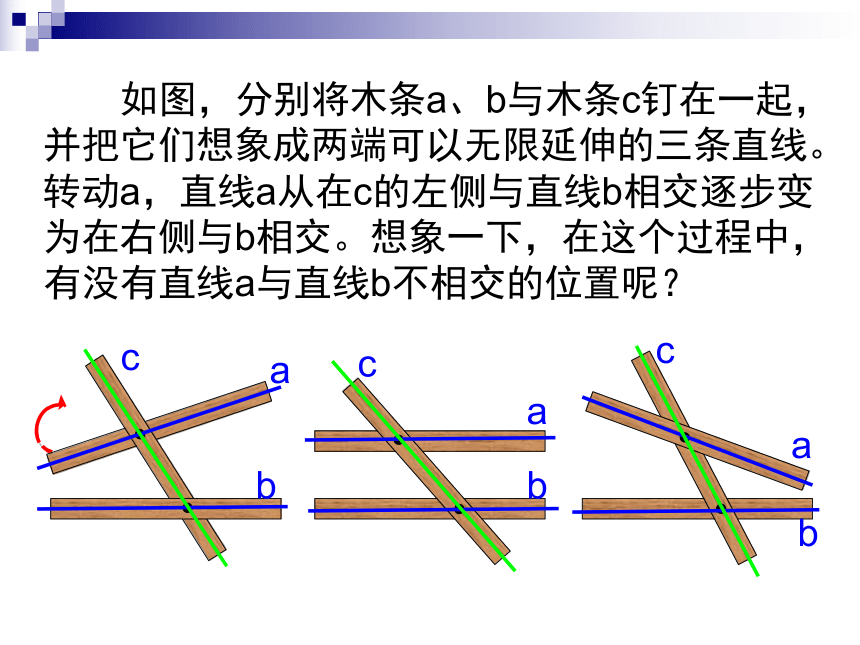
两只雪橇板的平行!5.2.1 平行线 如图,分别将木条a、b与木条c钉在一起,并把它们想象成两端可以无限延伸的三条直线。转动a,直线a从在c的左侧与直线b相交逐步变为在右侧与b相交。想象一下,在这个过程中,有没有直线a与直线b不相交的位置呢? 在木条转动过程中,存在一个直线a与直线b不相交的位置,这时直线a与b互相平行,记作a∥b。 平行线在生活中是很常见的,你还能举出其他一些例子吗?很多国家的国旗上都有平行线古巴国旗俄罗斯国旗比利时国旗荷兰国旗阿根廷国旗瑞士国旗看一看,它们有什么共同之处? 扶手双杠铁轨什么叫平行线? 在同一平面内,不相交的两条直线叫平行线.平行线的定义包含三层意思: (1)“在同一平面内”是前提条件,(2)“不相交”就是说两条直线没有交点,(3)平行线指的是“两条直线”而不是两条射线或两条线段.注意: 如何用几何语言描述平行呢?平行用符号“∥”表示,如:直线AB与直线CD平行,记作:AB∥CD,读作“AB平行于CD”。注意:平行线是相互的,使用平行符号“∥”时,可写成AB∥CD,也可以写成:CD∥AB。如果用a、b表示这两条直线,那么直线a与直线b平行,记作:a∥b.也可以写成: b ∥ a 。 在同一平面内,两条直线有几种位置关系?动手画一画?同一平面内两直线的位置关系:a⊥ba ∥b利用方格纸画平行线12345678如何画平行线?利用横线画
利用竖线画
利用对角线画
利用直尺与三角板画平行线如何画平行线?(1)放(2)靠(3)推(4)画●一放二靠三推四画 在转动木条a的过程中,有几个位置使得a与b平行?如图,过点B画直线a的平行线,能画出几条?再过点C画直线a的平行线,它和前面过点B画出的直线平行吗?讨论 1.如图:经过点B能画几条直线与直线a平行?a 经过直线外一点,有且只有一条直线和已知直线平行探究b 通过观察和画图,可以体验一个基本事实(平行公理): 2.过点C画一条直线与直线a平行,它与上题中所画的直线b平行吗?3.通过画图,你发现了什么? 如果两条直线都与第三条直线平行,那么这两条直线互相平行. 平行b 也就是说:如果b∥a,c∥a,那么b∥c。 如图,直线a ∥b,b∥c,c∥d,
那么a ∥d吗?为什么?abcd解: ∵ a ∥b,b∥c,
∴a ∥c (
)
∵ c∥d,
∴ a ∥d
如果两条直线都与第三条直线平行,
那么这两条直线互相平行。
(如果两条直线都与第三条直线平行,那么这两条直线互相平行。)
练一练不相交的直线就是平行线吗?在同一平面内不相交的直线就是平行线, 不在同一平面内不相交的直线不是平行线.练习:如图,长方体的各棱中,
与AB平行的棱有 ,
与AB相交的棱有 ,
与AB不平行也不相交的棱有 ,1.判断正错(正打“√”,错打“×” )
1.两条不相交的直线叫平行线.
2.在同一平面内的两条直线不平行就相交
3.一条直线的平行线有且只有一条
4.过一点,有且只有一条直线与这条直线平行
5.a,b,c是三条直线,如果a∥b且b∥c则a∥c练习一下:6.有且只有一个公共点的两直线是相交直线。2.在同一平面内,直线a与b满足下列条件:
a与b没有公共点,则a与b的位置关系_____。
a与b有且只有一个公共点,则a与b的位置关系___。
若AB∥CD且AB∥EF,______∥_____,理由是_______________________;平行相交CDEF平行公理推论3、下列说法中正确的是( )
A、在同一平面内,两条直线的位置
关系有相交、垂直、平行。
B、在同一平面内如果两条线段不相交,
那么这两条线段平行。
C、在同一平面内,不相交的两条射
线是平行线。
D、在同一平面内,不相交的两直线
是平行线。D4、下列语句中,正确的个数是( )
①不相交的两条直线是平行线
②同一平面内,两直线位置关系有两种,即相交或平行
③若线段AB与CD没有交点,则AB∥CD
④若a∥b,b∥c,则a与c不相交。
A、1个 B、2个 C、3个 D、4个B经过直线外一点,有且只有一条直线与这条直线平行5、已知直线l1与l2都经过点P,并且l1∥l3, l2∥l3,那么l1与l2必须重合,这是因为 . 1、在平面上有三条直线a , b , c ,
它们之间可能有哪几种位置关系?请画
图说明。(提示:从交点的个数考虑)
拓展延伸 同一平面内,三条直线的交点可以有 个.0或1或2或3 2.对于同一平面内的直线a、b、c,如果a∥b,c与a相交,那么c与b是什么位置关系?相交 3. 如图,AD∥BC,在 AB 上取一点 M,过点 M 作 MN∥BC,且交 CD 于点 N. 说明 MN 与 AD 的位置关系,为什么? 解:因为 AD∥BC,MN∥BC,
根据平行于同一直线的两直线
平行,可以得到 MN∥AD. 4. 在同一平面内有 4 条直线,这 4 条直线可以把这个平面分成几部分? (2) 当 4 条直线中只有三条直线两两平行时,可以把平面分成 8 部分. (3) 当 4 条直线仅有两条直线互相平行时,可以把整个平面分成 9 部分或 10 部分. (4) 当 4 条直线中有两条直线平行,另两条直线也平行时,可以把平面分成 9 部分. (5) 当 4 条直线任意两条都不平行时,可以把平面
分成 8 部分, 或 10 部分, 或 11 部分.
两只雪橇板的平行!5.2.1 平行线 如图,分别将木条a、b与木条c钉在一起,并把它们想象成两端可以无限延伸的三条直线。转动a,直线a从在c的左侧与直线b相交逐步变为在右侧与b相交。想象一下,在这个过程中,有没有直线a与直线b不相交的位置呢? 在木条转动过程中,存在一个直线a与直线b不相交的位置,这时直线a与b互相平行,记作a∥b。 平行线在生活中是很常见的,你还能举出其他一些例子吗?很多国家的国旗上都有平行线古巴国旗俄罗斯国旗比利时国旗荷兰国旗阿根廷国旗瑞士国旗看一看,它们有什么共同之处? 扶手双杠铁轨什么叫平行线? 在同一平面内,不相交的两条直线叫平行线.平行线的定义包含三层意思: (1)“在同一平面内”是前提条件,(2)“不相交”就是说两条直线没有交点,(3)平行线指的是“两条直线”而不是两条射线或两条线段.注意: 如何用几何语言描述平行呢?平行用符号“∥”表示,如:直线AB与直线CD平行,记作:AB∥CD,读作“AB平行于CD”。注意:平行线是相互的,使用平行符号“∥”时,可写成AB∥CD,也可以写成:CD∥AB。如果用a、b表示这两条直线,那么直线a与直线b平行,记作:a∥b.也可以写成: b ∥ a 。 在同一平面内,两条直线有几种位置关系?动手画一画?同一平面内两直线的位置关系:a⊥ba ∥b利用方格纸画平行线12345678如何画平行线?利用横线画
利用竖线画
利用对角线画
利用直尺与三角板画平行线如何画平行线?(1)放(2)靠(3)推(4)画●一放二靠三推四画 在转动木条a的过程中,有几个位置使得a与b平行?如图,过点B画直线a的平行线,能画出几条?再过点C画直线a的平行线,它和前面过点B画出的直线平行吗?讨论 1.如图:经过点B能画几条直线与直线a平行?a 经过直线外一点,有且只有一条直线和已知直线平行探究b 通过观察和画图,可以体验一个基本事实(平行公理): 2.过点C画一条直线与直线a平行,它与上题中所画的直线b平行吗?3.通过画图,你发现了什么? 如果两条直线都与第三条直线平行,那么这两条直线互相平行. 平行b 也就是说:如果b∥a,c∥a,那么b∥c。 如图,直线a ∥b,b∥c,c∥d,
那么a ∥d吗?为什么?abcd解: ∵ a ∥b,b∥c,
∴a ∥c (
)
∵ c∥d,
∴ a ∥d
如果两条直线都与第三条直线平行,
那么这两条直线互相平行。
(如果两条直线都与第三条直线平行,那么这两条直线互相平行。)
练一练不相交的直线就是平行线吗?在同一平面内不相交的直线就是平行线, 不在同一平面内不相交的直线不是平行线.练习:如图,长方体的各棱中,
与AB平行的棱有 ,
与AB相交的棱有 ,
与AB不平行也不相交的棱有 ,1.判断正错(正打“√”,错打“×” )
1.两条不相交的直线叫平行线.
2.在同一平面内的两条直线不平行就相交
3.一条直线的平行线有且只有一条
4.过一点,有且只有一条直线与这条直线平行
5.a,b,c是三条直线,如果a∥b且b∥c则a∥c练习一下:6.有且只有一个公共点的两直线是相交直线。2.在同一平面内,直线a与b满足下列条件:
a与b没有公共点,则a与b的位置关系_____。
a与b有且只有一个公共点,则a与b的位置关系___。
若AB∥CD且AB∥EF,______∥_____,理由是_______________________;平行相交CDEF平行公理推论3、下列说法中正确的是( )
A、在同一平面内,两条直线的位置
关系有相交、垂直、平行。
B、在同一平面内如果两条线段不相交,
那么这两条线段平行。
C、在同一平面内,不相交的两条射
线是平行线。
D、在同一平面内,不相交的两直线
是平行线。D4、下列语句中,正确的个数是( )
①不相交的两条直线是平行线
②同一平面内,两直线位置关系有两种,即相交或平行
③若线段AB与CD没有交点,则AB∥CD
④若a∥b,b∥c,则a与c不相交。
A、1个 B、2个 C、3个 D、4个B经过直线外一点,有且只有一条直线与这条直线平行5、已知直线l1与l2都经过点P,并且l1∥l3, l2∥l3,那么l1与l2必须重合,这是因为 . 1、在平面上有三条直线a , b , c ,
它们之间可能有哪几种位置关系?请画
图说明。(提示:从交点的个数考虑)
拓展延伸 同一平面内,三条直线的交点可以有 个.0或1或2或3 2.对于同一平面内的直线a、b、c,如果a∥b,c与a相交,那么c与b是什么位置关系?相交 3. 如图,AD∥BC,在 AB 上取一点 M,过点 M 作 MN∥BC,且交 CD 于点 N. 说明 MN 与 AD 的位置关系,为什么? 解:因为 AD∥BC,MN∥BC,
根据平行于同一直线的两直线
平行,可以得到 MN∥AD. 4. 在同一平面内有 4 条直线,这 4 条直线可以把这个平面分成几部分? (2) 当 4 条直线中只有三条直线两两平行时,可以把平面分成 8 部分. (3) 当 4 条直线仅有两条直线互相平行时,可以把整个平面分成 9 部分或 10 部分. (4) 当 4 条直线中有两条直线平行,另两条直线也平行时,可以把平面分成 9 部分. (5) 当 4 条直线任意两条都不平行时,可以把平面
分成 8 部分, 或 10 部分, 或 11 部分.
