【苏教版必修五教案】3.3 .1二元一次不等式表示的平面区域 教案2
文档属性
| 名称 | 【苏教版必修五教案】3.3 .1二元一次不等式表示的平面区域 教案2 |
|
|
| 格式 | rar | ||
| 文件大小 | 658.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-02-26 00:00:00 | ||
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
3.3 .1二元一次不等式表示的平面区域
【教学思路】:
一、创设情景,揭示课题
1.情境:下表给出了三种食物的维生素含量及成本:
维生素A(单位/kg) 维生素B
(单位/kg) 成 本(元)
X 300 700 5
Y 500 100 4
Z 300 300 3
某人欲将这三种食物混合成100kg的食品,要使混合食品中至少含35000单位的维生素及40000单位的维生素,设X、Y这两种食物各取kg、kg,那么应满足怎样的关系?
解答:∵X、Y这两种食物分别为kg、kg,∴食物为kg,则有
,即,
又∵,∴(介绍二元一次不等式的概念),
如果进一步要求如何取值时总成本最小呢?如何解决该问题.
问题转化为在以上不等式组约束下,求(介绍目标函数概念)的最大值问题.
要解决以上问题,我们首先要来了解二元一次不等式的几何意义.
2.问题:
坐标满足二元一次方程的点组成的图形是一条直线.怎样才能快速准确地画出直线呢?(学生答:描两点连成线.例如:该直线经过点和,画出经过两点的直线即为所求).教师问:怎样判断点在不在直线上呢?
结论:点的坐标满足直线的方程,则点在直线上;点的坐标不满足直线方程,则点不在直线上.
坐标满足不等式的点是否在直线上呢?这些点在哪儿呢?与直线的位置有什么关系呢?
二、研探新知
通过代特殊点的方法检验满足不等式的点的位置,并猜
想出结论:坐标满足不等式的点在直线的上方.
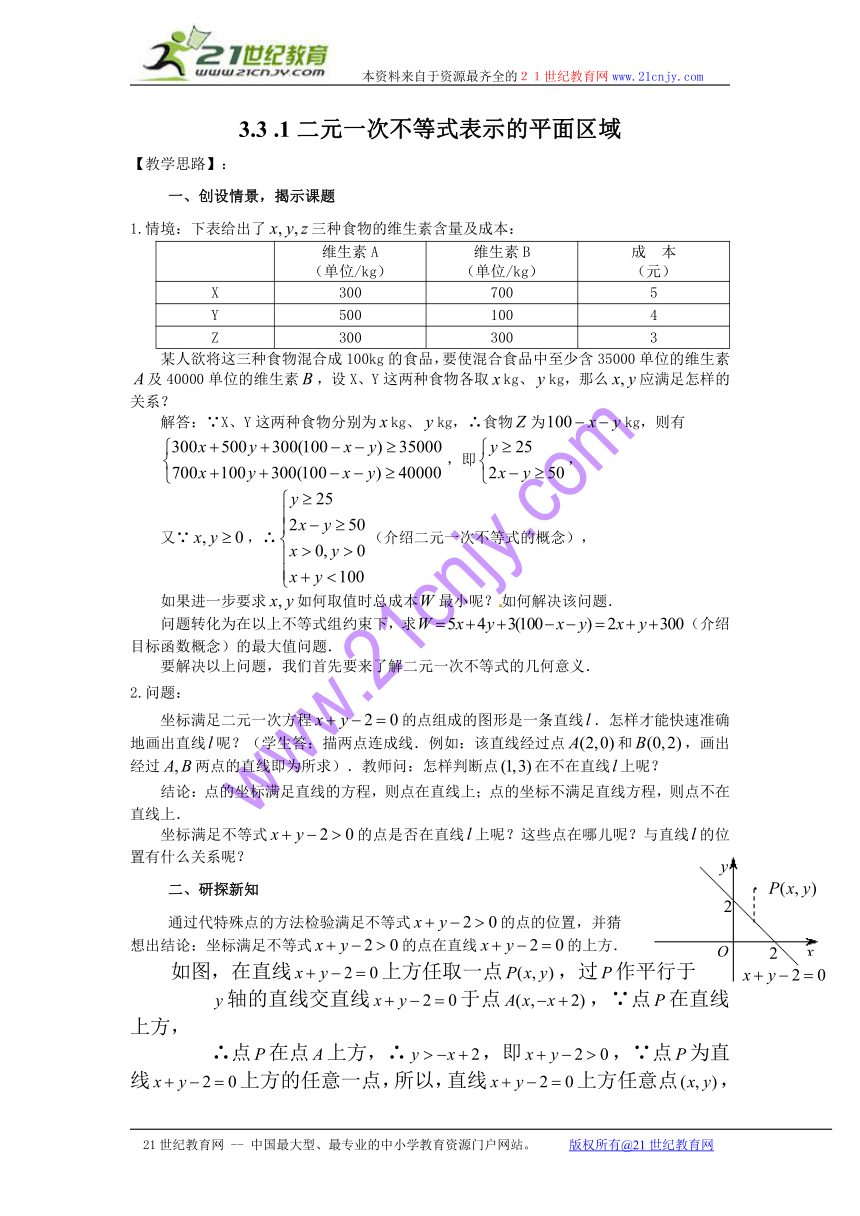
如图,在直线上方任取一点,过作平行于
轴的直线交直线于点,∵点在直线上方,
∴点在点上方,∴,即,∵点为直线上方的任意一点,所以,直线上方任意点,都有,即;同理,对于直线左下方任意点,都有,即.又∵平面上任意一点不在直线上即在直线上方或直线下方.因此,满足不等式的点在直线的上方,我们称不等式表示的是直线上方的平面区域;同样,不等式表示的是直线下方的平面区域.
学生练习:判断不等式表示的是直线上方还是下方的平面区域?(下方)
结论:①一般地, 在直角坐标系中,二元一次不等式表示某侧所有点组成的平面区域.我们把直线画成虚线,表示区域不包括边界.而不等式表示区域时则包括边界,把边界画成实线.
②一般地,直线把平面分成两个区域(如图):
表示直线上方的平面区域;
表示直线下方的平面区域.21世纪教育网
说明:(1)表示直线及直线上方的平面区域;表示直线及直线下方的平面区域.
(2)对于不含边界的区域,要将边界画成虚线.
三、质疑答辩,排难解惑,发展思维
例1(教材例1)画出下列不等式所表示的平面区域:(1);(2).
解:(1)(2)两个不等式所表示的平面区域如下图所示:
例2 判断下列不等式所表示的平面区域在相应直线的哪个区域?(用“上方”或“下方”填空)
(1)不等式表示直线 的平面区域;
(2)不等式表示直线 的平面区域;
(3)不等式表示直线 的平面区域;
(4)不等式表示直线 的平面区域.
说明:二元一次不等式在平面直角坐标系中表示某一侧所有点组成的平面区域.可以用“选点法”确定具体区域:任选一个不在直线上的点,检验它的坐标是否满足所给的不等式.若适合,则该点所在的一侧即为不等式所表示的平面区域;否则,直线的另一侧为所求的平面区域.
例3(1)若点在直线下方区域,则实数的取值范围为 .
(2)若点在直线的上方区域,则点在此直线的下方还是上方区域?
解:(1)∵直线下方的点的坐标满足,∴.
(2)∵直线的上方区域的点的坐标满足,∵点在直线的上方区域,∴,∴.又∵,∴点在此直线的上方区域.
例4(教材例2) 将下列各图中的平面区域(阴影部分)用不等式表示出来(其中图(1)中区域不包括轴):
解:(1);(2);(3).
例5 原点和点在直线的两侧,则实数的取值范围是 .
提示:将点和的坐标代入的符号相反,即,∴.
四、巩固深化,反馈矫正
五、归纳整理,整体认识
1.二元一次不等式的几何意义;二元一次不等式表示的平面区域.
2.二元一次不等式表示哪个平面区域的判断方法(二元一次不等式表示的平面区域的确定)
3.懂得画出二元一次不等式在平面区域中表示的图形
六、承上启下,留下悬念
1.由直线围成的三角形区域(包括边界)用不等式可表示为__
七、板书设计(略)
八、课后记:
下半平面
上半平面
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
3.3 .1二元一次不等式表示的平面区域
【教学思路】:
一、创设情景,揭示课题
1.情境:下表给出了三种食物的维生素含量及成本:
维生素A(单位/kg) 维生素B
(单位/kg) 成 本(元)
X 300 700 5
Y 500 100 4
Z 300 300 3
某人欲将这三种食物混合成100kg的食品,要使混合食品中至少含35000单位的维生素及40000单位的维生素,设X、Y这两种食物各取kg、kg,那么应满足怎样的关系?
解答:∵X、Y这两种食物分别为kg、kg,∴食物为kg,则有
,即,
又∵,∴(介绍二元一次不等式的概念),
如果进一步要求如何取值时总成本最小呢?如何解决该问题.
问题转化为在以上不等式组约束下,求(介绍目标函数概念)的最大值问题.
要解决以上问题,我们首先要来了解二元一次不等式的几何意义.
2.问题:
坐标满足二元一次方程的点组成的图形是一条直线.怎样才能快速准确地画出直线呢?(学生答:描两点连成线.例如:该直线经过点和,画出经过两点的直线即为所求).教师问:怎样判断点在不在直线上呢?
结论:点的坐标满足直线的方程,则点在直线上;点的坐标不满足直线方程,则点不在直线上.
坐标满足不等式的点是否在直线上呢?这些点在哪儿呢?与直线的位置有什么关系呢?
二、研探新知
通过代特殊点的方法检验满足不等式的点的位置,并猜
想出结论:坐标满足不等式的点在直线的上方.
如图,在直线上方任取一点,过作平行于
轴的直线交直线于点,∵点在直线上方,
∴点在点上方,∴,即,∵点为直线上方的任意一点,所以,直线上方任意点,都有,即;同理,对于直线左下方任意点,都有,即.又∵平面上任意一点不在直线上即在直线上方或直线下方.因此,满足不等式的点在直线的上方,我们称不等式表示的是直线上方的平面区域;同样,不等式表示的是直线下方的平面区域.
学生练习:判断不等式表示的是直线上方还是下方的平面区域?(下方)
结论:①一般地, 在直角坐标系中,二元一次不等式表示某侧所有点组成的平面区域.我们把直线画成虚线,表示区域不包括边界.而不等式表示区域时则包括边界,把边界画成实线.
②一般地,直线把平面分成两个区域(如图):
表示直线上方的平面区域;
表示直线下方的平面区域.21世纪教育网
说明:(1)表示直线及直线上方的平面区域;表示直线及直线下方的平面区域.
(2)对于不含边界的区域,要将边界画成虚线.
三、质疑答辩,排难解惑,发展思维
例1(教材例1)画出下列不等式所表示的平面区域:(1);(2).
解:(1)(2)两个不等式所表示的平面区域如下图所示:
例2 判断下列不等式所表示的平面区域在相应直线的哪个区域?(用“上方”或“下方”填空)
(1)不等式表示直线 的平面区域;
(2)不等式表示直线 的平面区域;
(3)不等式表示直线 的平面区域;
(4)不等式表示直线 的平面区域.
说明:二元一次不等式在平面直角坐标系中表示某一侧所有点组成的平面区域.可以用“选点法”确定具体区域:任选一个不在直线上的点,检验它的坐标是否满足所给的不等式.若适合,则该点所在的一侧即为不等式所表示的平面区域;否则,直线的另一侧为所求的平面区域.
例3(1)若点在直线下方区域,则实数的取值范围为 .
(2)若点在直线的上方区域,则点在此直线的下方还是上方区域?
解:(1)∵直线下方的点的坐标满足,∴.
(2)∵直线的上方区域的点的坐标满足,∵点在直线的上方区域,∴,∴.又∵,∴点在此直线的上方区域.
例4(教材例2) 将下列各图中的平面区域(阴影部分)用不等式表示出来(其中图(1)中区域不包括轴):
解:(1);(2);(3).
例5 原点和点在直线的两侧,则实数的取值范围是 .
提示:将点和的坐标代入的符号相反,即,∴.
四、巩固深化,反馈矫正
五、归纳整理,整体认识
1.二元一次不等式的几何意义;二元一次不等式表示的平面区域.
2.二元一次不等式表示哪个平面区域的判断方法(二元一次不等式表示的平面区域的确定)
3.懂得画出二元一次不等式在平面区域中表示的图形
六、承上启下,留下悬念
1.由直线围成的三角形区域(包括边界)用不等式可表示为__
七、板书设计(略)
八、课后记:
下半平面
上半平面
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
