1.1.2弧.度.制(改)
图片预览




文档简介
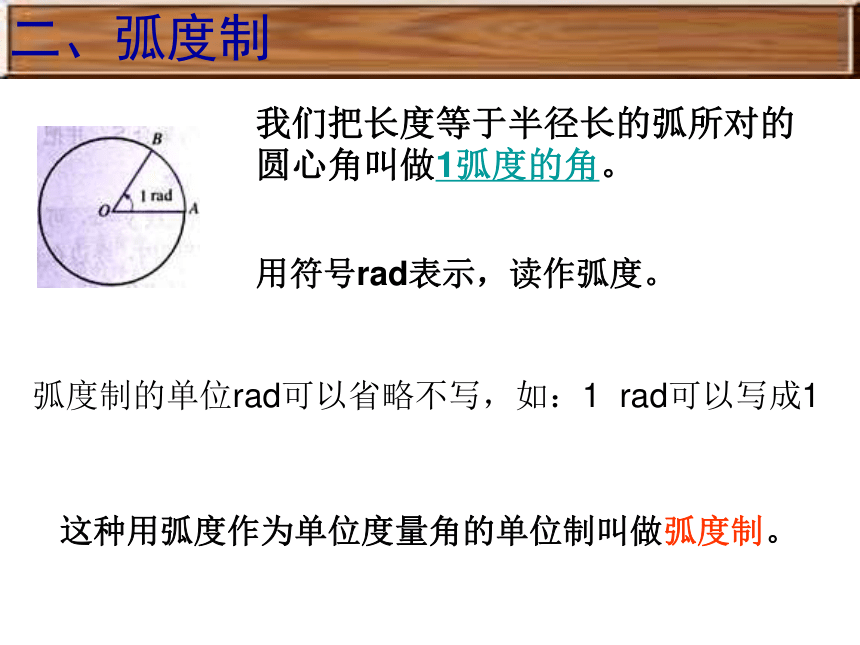
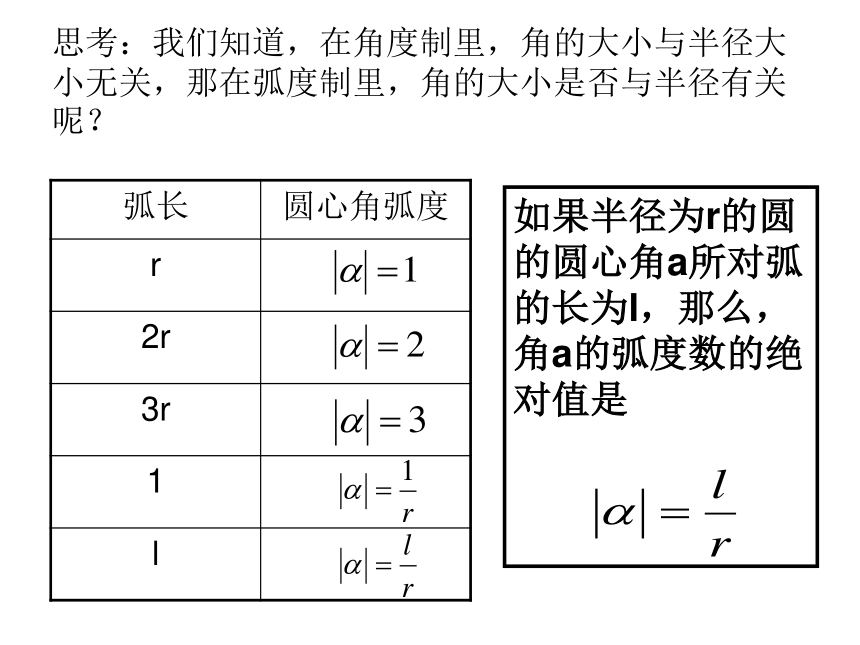
课件14张PPT。1.1.2 弧度制 3、在角度制下,当把两个带着度、分、秒为单位的角相加、相减时,由于运算进率不是十进制,总给我们带来不少困难.一、角度制 1、用“度”作单位来度量角的单位制称作 “角度制”,规定:圆周1/360的称作1°角。 2、角度制的单位有:度、分、秒。我们把长度等于半径长的弧所对的圆心角叫做1弧度的角。二、弧度制用符号rad表示,读作弧度。这种用弧度作为单位度量角的单位制叫做弧度制。弧度制的单位rad可以省略不写,如:1 rad可以写成1思考:我们知道,在角度制里,角的大小与半径大小无关,那在弧度制里,角的大小是否与半径有关呢?如果半径为r的圆的圆心角a所对弧的长为l,那么,角a的弧度数的绝对值是
弧度制与角度之间的关系思考:一个圆到底是多少弧度呢?为什么?解:∵一个圆对应的弧长为2πr,
∴其对应的圆心角的弧度说为:
∵一个圆的度数是360°,∴360°=2π,即:
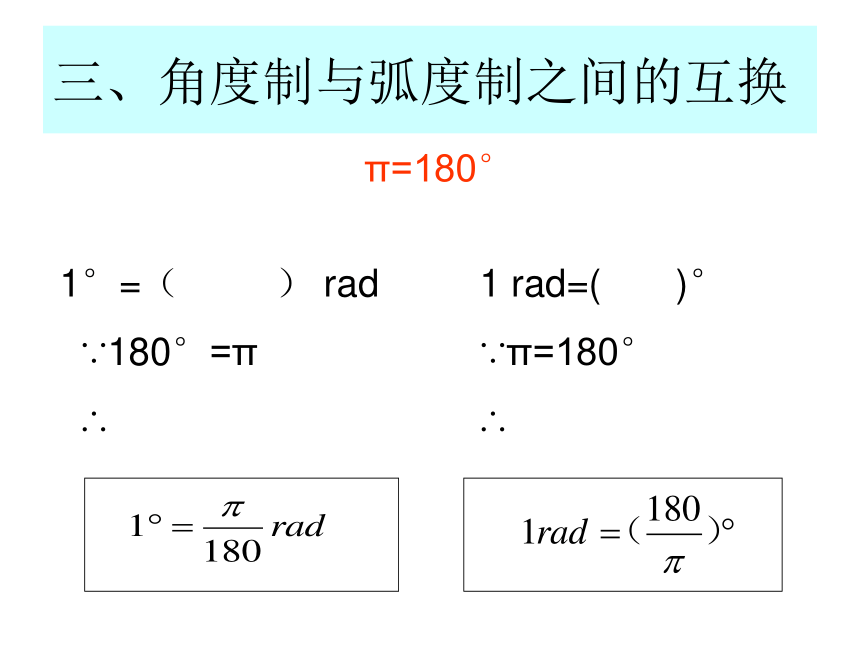
π=180°三、角度制与弧度制之间的互换π=180°1°=( ) rad
∵180°=π
∴1 rad=( )°
∵π=180°
∴
提问:弧度的大小是否与半径有关?为什么?完成课本P 6 探究的表格 思考:刚才的表格中提供OB旋转的方向有何作用? 一般地,正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0填写下列特殊角的度数和弧度数的对应表。提示:应尽快熟悉和习惯弧度制!四、例题讲解例1(1)把67°30′化成弧度制。
(2)把 化成角度制。解(1)∵67°30′=67.5°= ,
又∵1°=
∴67°30′=67.5 =
(2) = 180°=405°练习:P 9 1,2例2:将下列弧度制表示的角化为2kπ+α(k∈Z,α∈[0,2π))的形式,并指出它们所在的象限。(1) (2) 解(1) ,∴ 为第一象限角
(2) ,∴ 为第二象限角练习:P 9 6, 3, 5 P 10 6作业: P 10 7(1)(2) 8(1)(2)1.1弧度角:2.弧度的计算公式:3.弧度与角度的换算: 把长度等于半径长的弧所对的圆心角叫做1弧度的角,
弧度制与角度之间的关系思考:一个圆到底是多少弧度呢?为什么?解:∵一个圆对应的弧长为2πr,
∴其对应的圆心角的弧度说为:
∵一个圆的度数是360°,∴360°=2π,即:
π=180°三、角度制与弧度制之间的互换π=180°1°=( ) rad
∵180°=π
∴1 rad=( )°
∵π=180°
∴
提问:弧度的大小是否与半径有关?为什么?完成课本P 6 探究的表格 思考:刚才的表格中提供OB旋转的方向有何作用? 一般地,正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0填写下列特殊角的度数和弧度数的对应表。提示:应尽快熟悉和习惯弧度制!四、例题讲解例1(1)把67°30′化成弧度制。
(2)把 化成角度制。解(1)∵67°30′=67.5°= ,
又∵1°=
∴67°30′=67.5 =
(2) = 180°=405°练习:P 9 1,2例2:将下列弧度制表示的角化为2kπ+α(k∈Z,α∈[0,2π))的形式,并指出它们所在的象限。(1) (2) 解(1) ,∴ 为第一象限角
(2) ,∴ 为第二象限角练习:P 9 6, 3, 5 P 10 6作业: P 10 7(1)(2) 8(1)(2)1.1弧度角:2.弧度的计算公式:3.弧度与角度的换算: 把长度等于半径长的弧所对的圆心角叫做1弧度的角,
