1.3.2秦九韶算法
图片预览








文档简介
课件22张PPT。1.3算法案例第二课时
秦九韶算法1、求两个数的最大公约数的两种方法分别是( )和( )。
2、两个数21672,8127的最大公约数是 ( )
A、2709 B、2606 C、2703 D、2706课前复习[问题1]:设计求多项式f(x)=2x5-5x4-4x3+3x2-6x+7当x=5时的值的算法,并写出程序. 点评:上述算法一共做了15次乘法运算,5次加法运算.优点是简单,易懂;缺点是不通用,不能解决任意多项多求值问题,而且计算效率不高.新课引入[问题2]:能否探索更好的算法,来解决任意多项式的求值问题?f(x)=2x5-5x4-4x3+3x2-6x+7
=(2x4-5x3-4x2+3x-6)x+7
=((2x3-5x2-4x+3)x-6)x+7
=(((2x2-5x-4)x+3)x-6)x+7
=((((2x-5)x-4)x+3)x-6)x+7
v0=2
v1=v0x-5=2×5-5=5
v2=v1x-4=5×5-4=21
v3=v2x+3=21×5+3=108
v4=v3x-6=108×5-6=534
v5=v4x+7=534×5+7=2677所以,当x=5时,多项式的值是2677.这种求多项式值的方法就叫秦九韶算法.新课引入秦九韶《数书九章》.例1:用秦九韶算法求多项式 f(x)=2x5-5x4-4x3+3x2-6x+7当x=5时的值.解法一:首先将原多项式改写成如下形式 : f(x)=((((2x-5)x-4)x+3)x-6)x+7v0=2 v1=v0x-5=2×5-5=5
v2=v1x-4=5×5-4=21
v3=v2x+3=21×5+3=108
v4=v3x-6=108×5-6=534
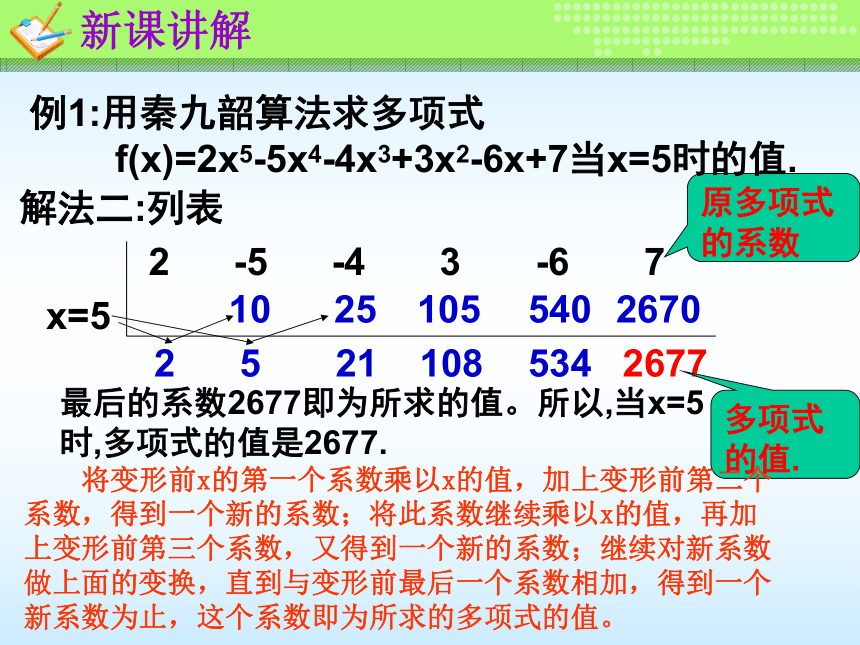
v5=v4x+7=534×5+7=2677所以,当x=5时,多项式的值是2677.然后由内向外逐层计算一次多项式的值,即新课引入用秦九韶算法求多项式的值,与多项式的组成由直接的关系吗?用秦九韶算法求上述多项式的值,需要多少次乘法运算和多少次加法运算? 在求值的过程中,计算只与多项式的系数有关。共做了5次乘法运算,5次加法运算。把高次幂的运算转化为简单的加和乘的运算2 -5 -4 3 -6 7x=5105252110510854053426702677最后的系数2677即为所求的值。所以,当x=5时,多项式的值是2677.原多项式的系数多项式的值.例1:用秦九韶算法求多项式 f(x)=2x5-5x4-4x3+3x2-6x+7当x=5时的值.解法二:列表2新课讲解 将变形前x的第一个系数乘以x的值,加上变形前第二个系数,得到一个新的系数;将此系数继续乘以x的值,再加上变形前第三个系数,又得到一个新的系数;继续对新系数做上面的变换,直到与变形前最后一个系数相加,得到一个新系数为止,这个系数即为所求的多项式的值。自我测评42 -5 0 -4 3 -6 0x=5105252512512160560830403034所以,当x=5时,多项式的值是15170.练一练:用秦九韶算法求多项式 f(x)=2x6-5x5-4x3+3x2-6x当x=5时的值.解:原多项式先化为:
f(x)=2x6-5x5 +0×x4-4x3+3x2-6x+0
列表21517015170 注意:n次多项式有n+1项,因此缺少哪一项应将其系数补0.新课讲解f(x)=anxn+an-1xn-1+an-2xn-2+……+a1x+a0.我们可以改写成如下形式:f(x)=(…(anx+an-1)x+an-2)x+…+a1)x+a0. 求多项式的值时,首先计算最内层括号内一次多项式的值,即
v1=anx+an-1,然后由内向外逐层计算一次多项式的值,即 一般地,对于一个n次多项式v2=v1x+an-2,v3=v2x+an-3, ……,vn=vn-1x+a0. 这样,求n次多项式f(x)的值就转化为求n个一次多项式的值.这种算法称为秦九韶算法. 点评:秦九韶算法是求一元多项式的值的一种方法.
它的特点是:把求一个n次多项式的值转化为求n个一次多项式的值,通过这种转化,把运算的次数由至多n(n+1)/2次乘法运算和n次加法运算,减少为n次乘法运算和n次加法运算,大大提高了运算效率.秦九韶算法的特点及注意事项:特点: 通过一次式的反复计算,有规律的推算出下一个值,从而计算高次多项式的值,这种算法也称为“递推法”.对于一个n次多项式当最高次项的系数不为1时,需进行 次乘法;若各项均不为零,则需进行 次加法(或减法),缺几项减去几.nn注意:若多项式函数中间出现空项,要以系数为0补齐此项,即0×xm随堂训练:1、用秦九韶算法计算多项式当x=0.4时的值时,需要做乘法和加法的次数分别是( )A 6,6 B 5,6 C 5,5 D 6,5AD自我测评3v1=anx+an-1,v2=v1x+an-2,v3=v2x+an-3, ……,vn=vn-1x+a0. 观察上述秦九韶算法中的n个一次式,可见vk的计算要用到vk-1的值.若令v0=an,得 这是一个在秦九韶算法中反复执行的步骤,因此可用循环结构来实现.第一步,输入多项式次数n、最高次项的系数an和x的值
第二步,将v的值初始化为an,将i的值初始化为n-1
第三步,输入i次项的系数ai
第四步,v=vx+ai,i=i-1
第五步,若i>=0,则返回第三步,否则输出v算法分析:否程序框图开始输入n,an,x的值输入aii>=0?i=n-1v=anv=vx+aii=i-1输出v结束是课后作业:
秦九韶算法1、求两个数的最大公约数的两种方法分别是( )和( )。
2、两个数21672,8127的最大公约数是 ( )
A、2709 B、2606 C、2703 D、2706课前复习[问题1]:设计求多项式f(x)=2x5-5x4-4x3+3x2-6x+7当x=5时的值的算法,并写出程序. 点评:上述算法一共做了15次乘法运算,5次加法运算.优点是简单,易懂;缺点是不通用,不能解决任意多项多求值问题,而且计算效率不高.新课引入[问题2]:能否探索更好的算法,来解决任意多项式的求值问题?f(x)=2x5-5x4-4x3+3x2-6x+7
=(2x4-5x3-4x2+3x-6)x+7
=((2x3-5x2-4x+3)x-6)x+7
=(((2x2-5x-4)x+3)x-6)x+7
=((((2x-5)x-4)x+3)x-6)x+7
v0=2
v1=v0x-5=2×5-5=5
v2=v1x-4=5×5-4=21
v3=v2x+3=21×5+3=108
v4=v3x-6=108×5-6=534
v5=v4x+7=534×5+7=2677所以,当x=5时,多项式的值是2677.这种求多项式值的方法就叫秦九韶算法.新课引入秦九韶《数书九章》.例1:用秦九韶算法求多项式 f(x)=2x5-5x4-4x3+3x2-6x+7当x=5时的值.解法一:首先将原多项式改写成如下形式 : f(x)=((((2x-5)x-4)x+3)x-6)x+7v0=2 v1=v0x-5=2×5-5=5
v2=v1x-4=5×5-4=21
v3=v2x+3=21×5+3=108
v4=v3x-6=108×5-6=534
v5=v4x+7=534×5+7=2677所以,当x=5时,多项式的值是2677.然后由内向外逐层计算一次多项式的值,即新课引入用秦九韶算法求多项式的值,与多项式的组成由直接的关系吗?用秦九韶算法求上述多项式的值,需要多少次乘法运算和多少次加法运算? 在求值的过程中,计算只与多项式的系数有关。共做了5次乘法运算,5次加法运算。把高次幂的运算转化为简单的加和乘的运算2 -5 -4 3 -6 7x=5105252110510854053426702677最后的系数2677即为所求的值。所以,当x=5时,多项式的值是2677.原多项式的系数多项式的值.例1:用秦九韶算法求多项式 f(x)=2x5-5x4-4x3+3x2-6x+7当x=5时的值.解法二:列表2新课讲解 将变形前x的第一个系数乘以x的值,加上变形前第二个系数,得到一个新的系数;将此系数继续乘以x的值,再加上变形前第三个系数,又得到一个新的系数;继续对新系数做上面的变换,直到与变形前最后一个系数相加,得到一个新系数为止,这个系数即为所求的多项式的值。自我测评42 -5 0 -4 3 -6 0x=5105252512512160560830403034所以,当x=5时,多项式的值是15170.练一练:用秦九韶算法求多项式 f(x)=2x6-5x5-4x3+3x2-6x当x=5时的值.解:原多项式先化为:
f(x)=2x6-5x5 +0×x4-4x3+3x2-6x+0
列表21517015170 注意:n次多项式有n+1项,因此缺少哪一项应将其系数补0.新课讲解f(x)=anxn+an-1xn-1+an-2xn-2+……+a1x+a0.我们可以改写成如下形式:f(x)=(…(anx+an-1)x+an-2)x+…+a1)x+a0. 求多项式的值时,首先计算最内层括号内一次多项式的值,即
v1=anx+an-1,然后由内向外逐层计算一次多项式的值,即 一般地,对于一个n次多项式v2=v1x+an-2,v3=v2x+an-3, ……,vn=vn-1x+a0. 这样,求n次多项式f(x)的值就转化为求n个一次多项式的值.这种算法称为秦九韶算法. 点评:秦九韶算法是求一元多项式的值的一种方法.
它的特点是:把求一个n次多项式的值转化为求n个一次多项式的值,通过这种转化,把运算的次数由至多n(n+1)/2次乘法运算和n次加法运算,减少为n次乘法运算和n次加法运算,大大提高了运算效率.秦九韶算法的特点及注意事项:特点: 通过一次式的反复计算,有规律的推算出下一个值,从而计算高次多项式的值,这种算法也称为“递推法”.对于一个n次多项式当最高次项的系数不为1时,需进行 次乘法;若各项均不为零,则需进行 次加法(或减法),缺几项减去几.nn注意:若多项式函数中间出现空项,要以系数为0补齐此项,即0×xm随堂训练:1、用秦九韶算法计算多项式当x=0.4时的值时,需要做乘法和加法的次数分别是( )A 6,6 B 5,6 C 5,5 D 6,5AD自我测评3v1=anx+an-1,v2=v1x+an-2,v3=v2x+an-3, ……,vn=vn-1x+a0. 观察上述秦九韶算法中的n个一次式,可见vk的计算要用到vk-1的值.若令v0=an,得 这是一个在秦九韶算法中反复执行的步骤,因此可用循环结构来实现.第一步,输入多项式次数n、最高次项的系数an和x的值
第二步,将v的值初始化为an,将i的值初始化为n-1
第三步,输入i次项的系数ai
第四步,v=vx+ai,i=i-1
第五步,若i>=0,则返回第三步,否则输出v算法分析:否程序框图开始输入n,an,x的值输入aii>=0?i=n-1v=anv=vx+aii=i-1输出v结束是课后作业:
