高中数学数形结合思想专题

课件18张PPT。 数形结合的思想方法　　数学是研究数量关系和空间形式的科学，“数”与“形”及它们的联系与转化是数学研究永恒的主题。从“数”“形”两个方面对数学问题进行分析，既注重“数”的严谨性，又充分发挥“形”的直观性。“以数解形，以形助数”，也是高考中必考的思想方法。
　　前言引言
（1）函数中的数形结合思想；
（2）不等式中的数形结合思想；
（3）数列中的数形结合思想；
（4)向量中的数形结合思想；
（5）复数中的数形结合思想；
（6）解析几何中的数形结合思想；
基本内容数形结合的基本思路 根据数的结构特征，构造出与之相应的几何图形，并利用图形的特性和规律，解决数的问题；(以形助数）
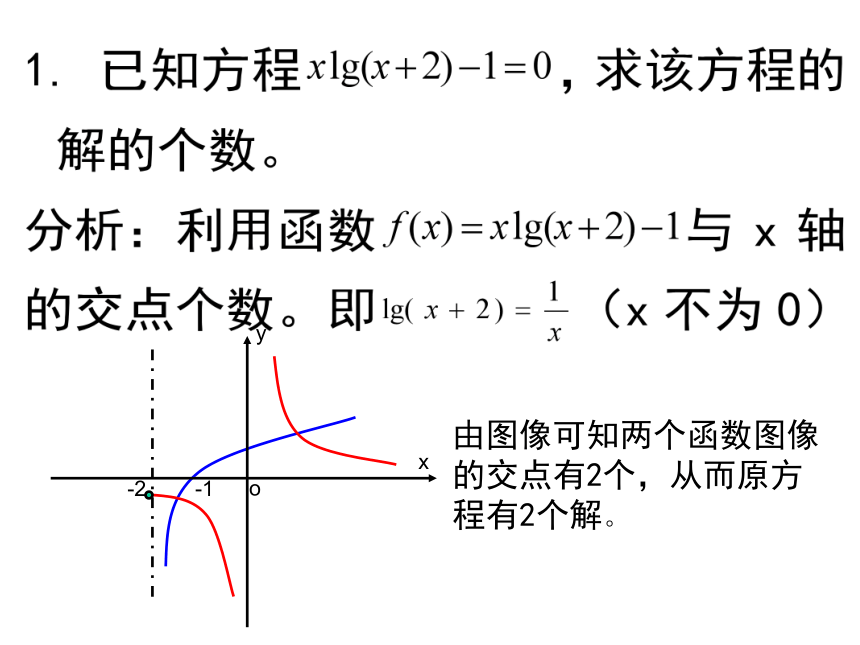
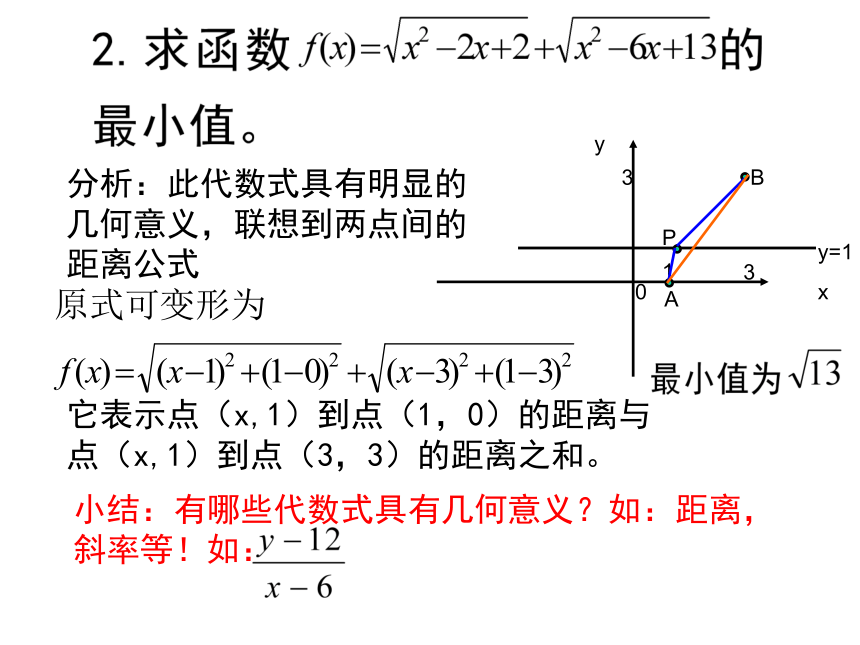
将图形信息转化成代数信息，使解决形的问题转化为数量关系的问题。（以数解形）四、典型示范(函数中)基础训练(函数）由图像可知两个函数图像的交点有2个，从而原方程有2个解。它表示点（x,1）到点（1，0）的距离与点（x,1）到点（3，3）的距离之和。分析：此代数式具有明显的几何意义，联想到两点间的距离公式小结：有哪些代数式具有几何意义？如：距离，斜率等！如：P(6,12)解：解法小结：数形结合法2(附加）3四、典型示范（不等式中）基础训练（不等式）四、典型示范（不等式中）四、典型示范（数列中）基础训练（数列）四、典型示范（数列中）方法二：图像法12四、典型示范（向量中）基础训练（向量）方法二：图像法四、典型示范（复数中）基础训练（复数）定义法P四、典型示范（解析几何中）基础训练（解析几何）xyoPMC解法小结：数形结合法
利用几何性质解决六、规律总结二 数形结合思想简言之就是“代数问题几何化，几何问题代数化”，充分体现图形的直观性，代数推理的合理性。解题时不能单纯用图形的直观代替严密的逻辑推理。一 实现数形结合，常与下列内容有关：
（1）函数与图像的对应关系；
（2）方程与曲线的对应关系；
（3）以几何元素和几何条件为背景建立起来的概念,如三角函数，向量等；
（4）所给的等式或代数式有明显的几何意义，如斜率，截距，距离等。课堂小结GOODBYE