圆与圆位置关系
图片预览



文档简介
课件27张PPT。25.7圆与圆的位置关系通过前面的学习我们了解了点与圆的位置关系以及直线与圆的位置关系,那么圆与圆又有什么样的位置关系呢?又是怎样区分的呢?
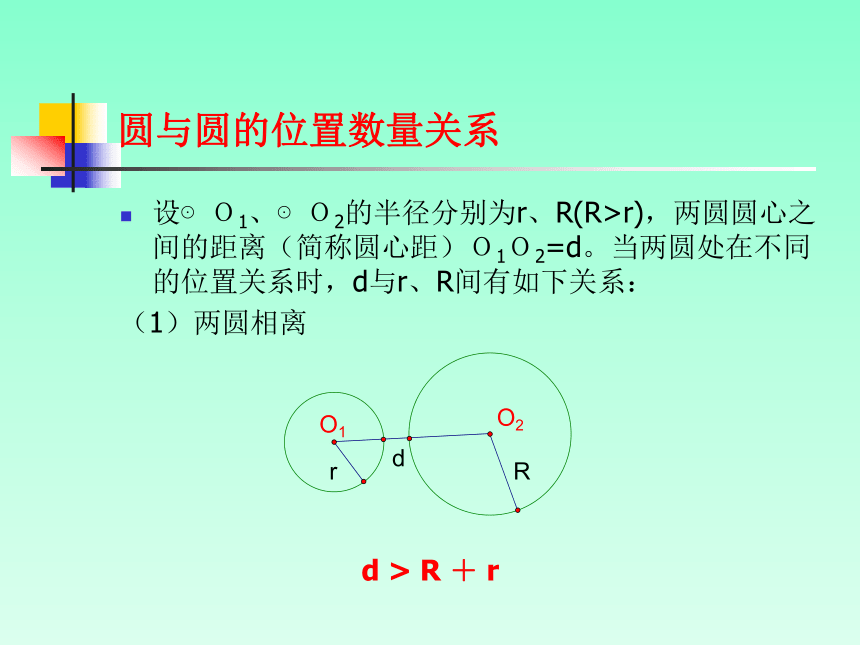
外离外切相交内切内含圆与圆的位置数量关系设⊙O1、⊙O2的半径分别为r、R(R>r),两圆圆心之间的距离(简称圆心距)O1O2=d。当两圆处在不同的位置关系时,d与r、R间有如下关系:
(1)两圆相离
d > R + r
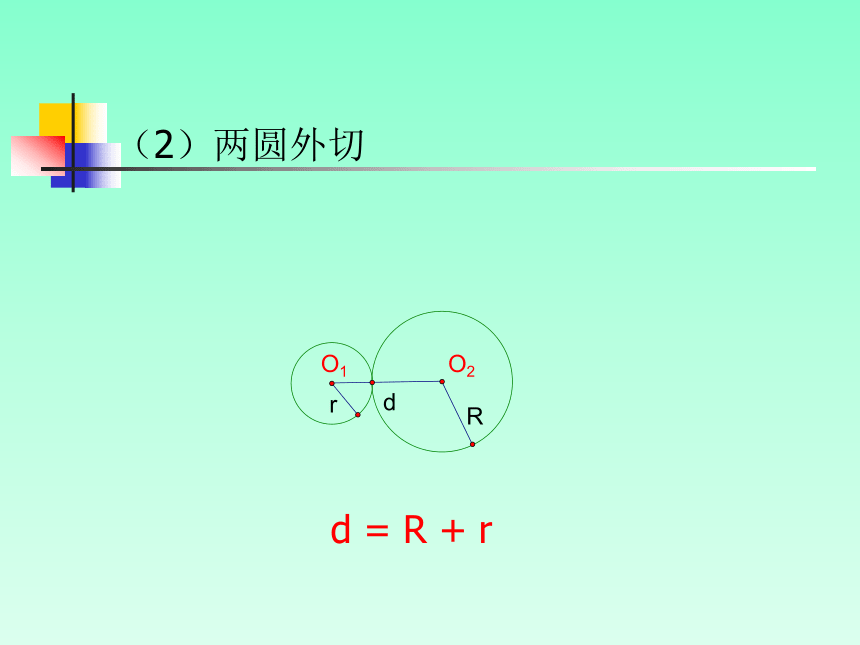
(2)两圆外切
d = R + r
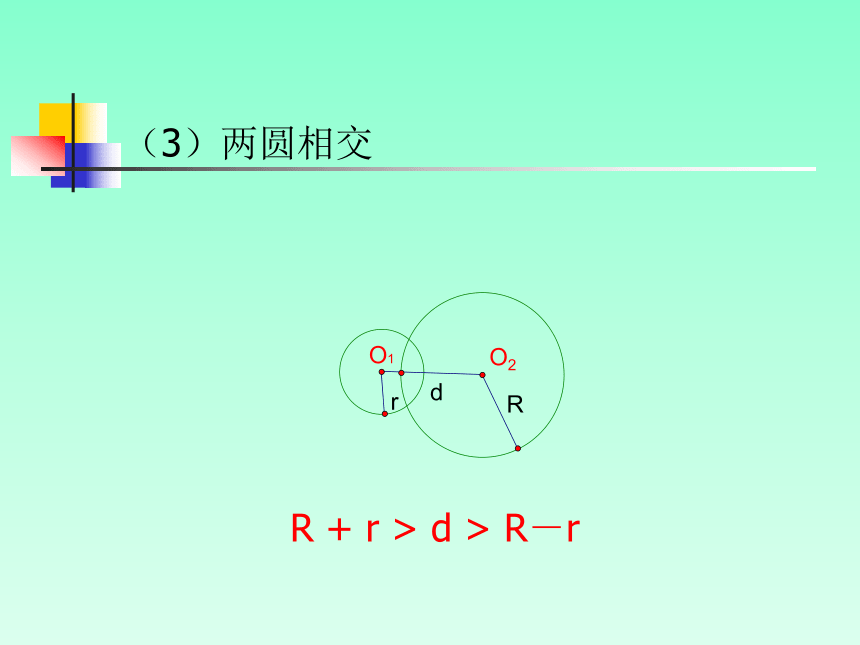
(3)两圆相交
R + r > d > R-r
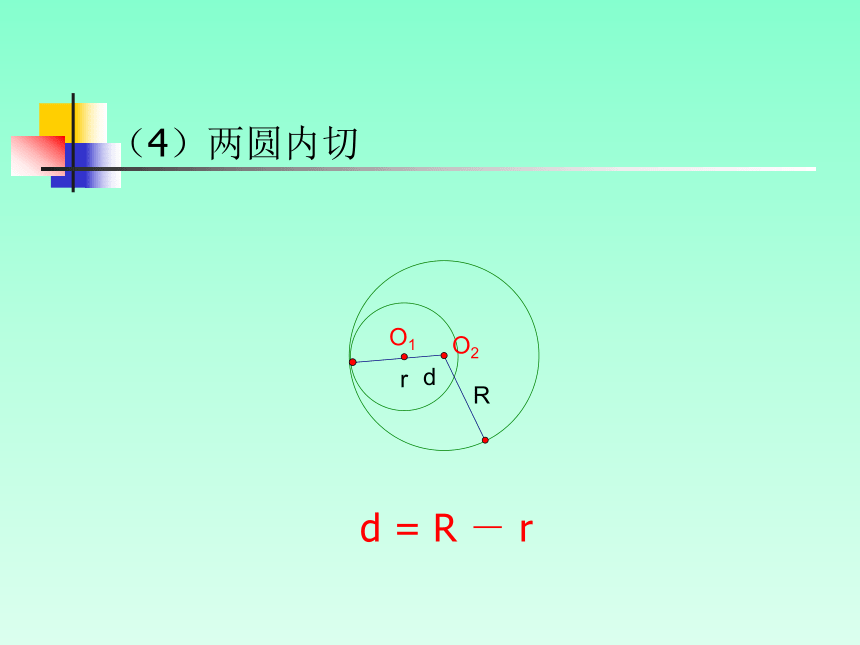
(4)两圆内切
d = R - r
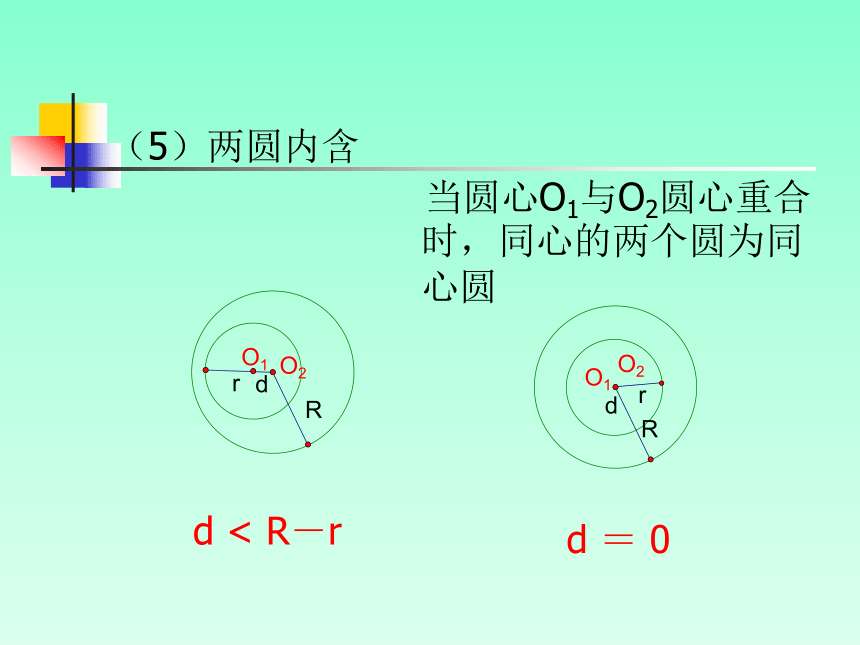
(5)两圆内含
d < R-r
当圆心O1与O2圆心重合时,同心的两个圆为同心圆d = 0课堂演练 1. ⊙O1、⊙O2的半径分别为r=3cm,R=4cm.若设:
⑴O1O2=8cm ⑵O1O2=7cm
⑶O1O2=5cm ⑷O1O2=1cm
⑸O1O2=0.5cm ⑹O1O2=0cm
2.定圆O的半径是4厘米,同一平面内动圆P的半径是1厘米,当点P向点O移动时:
⑴OP多长,两圆相交?
⑵OP多长,两圆相切?
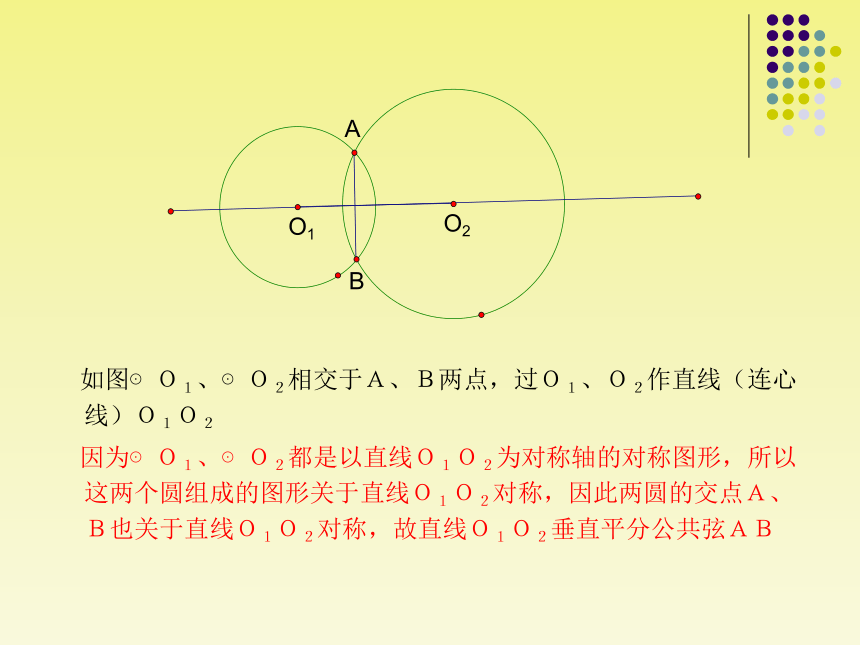
如图⊙O1、⊙O2相交于A、B两点,过O1、O2作直线(连心线)O1O2
因为⊙O1、⊙O2都是以直线O1O2为对称轴的对称图形,所以这两个圆组成的图形关于直线O1O2对称,因此两圆的交点A、B也关于直线O1O2对称,故直线O1O2垂直平分公共弦AB
由此可得
定理 两圆相交时,连心线垂直平分两圆的
公共弦
当两圆的交点A、B重合为一点时,这唯一
的公共点叫切点.因此有
定理 两圆相切时,连心线通过切点
演示两圆的位置关系外离外切相交内切内含12345演示两圆外离>两圆外切两圆相交两圆内切两圆内含=<=< < ddddd例2: 求证:如果两圆相切,那么其中任一个圆的过两圆切点的切线,也必是另一个圆的切线. 分析:分两种情况讨论,
一、当两圆外切时,
二、当两圆内切时。 依据:两圆相切,连心线必过切点。 例3: 如图,⊙O的半径为5cm,点P是⊙O外一点,OP =8cm,求(1)以P为圆心作⊙P与⊙O内切,大圆⊙P的半径是多少?(2)以P为圆心作⊙P与⊙O内切,大圆⊙P的半径是多少? 解: (1)设⊙O与⊙P外切于点A,则
PA=OP-OA
PA=3cm.
(2)设⊙O 与⊙P内切于点B,则
PB=OP+OB
PB=13cm.判别两圆关系1. 若两圆的圆心距两圆半径是方程两根,则两圆位置关系为 .外离2. 若两圆的半径为圆心距 满足则两圆位置关系为 .外切或内切
.内含4、相交两圆的半径分别为8cm和
5cm,公共弦长为8cm,则两圆的
圆心距为 。4练习5、已知两个等圆相交于A、B,
⊙O1经过点O2,求∠O1AB的度数。练习6、已知:A是⊙O1、⊙O2的一个交点,点P是O1 O2的中点,过点A的直线MN垂直于PA,交⊙O1、 ⊙ O2于M、N。
求证:AM=AN。练习例4: 已知⊙的半径为(1) ⊙⊙外切,则 的半径为 .⊙ 已知⊙的半径为变(一)轨迹或3cm为半径的圆O点为圆心7cm外离圆和圆的五种位置关系O1O2 > R+rO1O2 = R+rR- r < O1O2 < R+rO1O2 = R-r0 ≤ O1O2 < R-rO1O2 = 0外切相交内切内含同心圆(一种特殊的内含)相切两圆的性质1、通过两圆圆心的直线叫做连心线。
2、如果两个圆相切,那么切点一定
在连心线上。连心线:是指通过两圆圆心的一条直线。分析:连心线是它的对称轴。两圆相切时,由
于切点是它们唯一的公共点,所以切点一定在对
称轴上。敬请指导点与圆的位置关系图1图2图3返回直线和圆的位置关系返回直线与圆的位置关系图1图2图3返回
外离外切相交内切内含圆与圆的位置数量关系设⊙O1、⊙O2的半径分别为r、R(R>r),两圆圆心之间的距离(简称圆心距)O1O2=d。当两圆处在不同的位置关系时,d与r、R间有如下关系:
(1)两圆相离
d > R + r
(2)两圆外切
d = R + r
(3)两圆相交
R + r > d > R-r
(4)两圆内切
d = R - r
(5)两圆内含
d < R-r
当圆心O1与O2圆心重合时,同心的两个圆为同心圆d = 0课堂演练 1. ⊙O1、⊙O2的半径分别为r=3cm,R=4cm.若设:
⑴O1O2=8cm ⑵O1O2=7cm
⑶O1O2=5cm ⑷O1O2=1cm
⑸O1O2=0.5cm ⑹O1O2=0cm
2.定圆O的半径是4厘米,同一平面内动圆P的半径是1厘米,当点P向点O移动时:
⑴OP多长,两圆相交?
⑵OP多长,两圆相切?
如图⊙O1、⊙O2相交于A、B两点,过O1、O2作直线(连心线)O1O2
因为⊙O1、⊙O2都是以直线O1O2为对称轴的对称图形,所以这两个圆组成的图形关于直线O1O2对称,因此两圆的交点A、B也关于直线O1O2对称,故直线O1O2垂直平分公共弦AB
由此可得
定理 两圆相交时,连心线垂直平分两圆的
公共弦
当两圆的交点A、B重合为一点时,这唯一
的公共点叫切点.因此有
定理 两圆相切时,连心线通过切点
演示两圆的位置关系外离外切相交内切内含12345演示两圆外离>两圆外切两圆相交两圆内切两圆内含=<=< < ddddd例2: 求证:如果两圆相切,那么其中任一个圆的过两圆切点的切线,也必是另一个圆的切线. 分析:分两种情况讨论,
一、当两圆外切时,
二、当两圆内切时。 依据:两圆相切,连心线必过切点。 例3: 如图,⊙O的半径为5cm,点P是⊙O外一点,OP =8cm,求(1)以P为圆心作⊙P与⊙O内切,大圆⊙P的半径是多少?(2)以P为圆心作⊙P与⊙O内切,大圆⊙P的半径是多少? 解: (1)设⊙O与⊙P外切于点A,则
PA=OP-OA
PA=3cm.
(2)设⊙O 与⊙P内切于点B,则
PB=OP+OB
PB=13cm.判别两圆关系1. 若两圆的圆心距两圆半径是方程两根,则两圆位置关系为 .外离2. 若两圆的半径为圆心距 满足则两圆位置关系为 .外切或内切
.内含4、相交两圆的半径分别为8cm和
5cm,公共弦长为8cm,则两圆的
圆心距为 。4练习5、已知两个等圆相交于A、B,
⊙O1经过点O2,求∠O1AB的度数。练习6、已知:A是⊙O1、⊙O2的一个交点,点P是O1 O2的中点,过点A的直线MN垂直于PA,交⊙O1、 ⊙ O2于M、N。
求证:AM=AN。练习例4: 已知⊙的半径为(1) ⊙⊙外切,则 的半径为 .⊙ 已知⊙的半径为变(一)轨迹或3cm为半径的圆O点为圆心7cm外离圆和圆的五种位置关系O1O2 > R+rO1O2 = R+rR- r < O1O2 < R+rO1O2 = R-r0 ≤ O1O2 < R-rO1O2 = 0外切相交内切内含同心圆(一种特殊的内含)相切两圆的性质1、通过两圆圆心的直线叫做连心线。
2、如果两个圆相切,那么切点一定
在连心线上。连心线:是指通过两圆圆心的一条直线。分析:连心线是它的对称轴。两圆相切时,由
于切点是它们唯一的公共点,所以切点一定在对
称轴上。敬请指导点与圆的位置关系图1图2图3返回直线和圆的位置关系返回直线与圆的位置关系图1图2图3返回
