双曲线
图片预览








文档简介
课件21张PPT。双曲线及标准方程一、回顾1.椭圆的第一定义是什么?
2.椭圆的标准方程、焦点坐标是什么?y|MF1|+|MF2|=2a(2a>|F1F2|)a2=b2+c2
F ( ±c,0) F(0, ± c)
双曲线的定义平面内与两定点F1`F2的距离的差的绝对值等于常数(小于|F1F2 | )的点的轨迹叫做双曲线。
这两个定点叫做双曲线的焦点,
两焦点的距离叫做双曲线的焦距。 双曲线的一支
两条射线 1、平面内与两定点F1,F2的距离的差等于常数(小于 |F1F2 | )的点的轨迹是什么?2、若常数2a=0,轨迹是什么?
3、若常数2a= |F1F2|轨迹是什么?垂直平分线椭圆:平面内与两定点 F 1、F2的距离之和等
于常数( 大于 | F 1F2 | ) 的点的轨迹叫做椭圆。
这两定点叫做椭圆的焦点,两焦点的距离叫椭
圆的焦距。双曲线:平面内与两定点 F 1、F2的距离的差
的绝对值等于常数( 小于 | F 1F2 | ) 的点的轨迹
叫做双曲线。这两定点叫做双曲线的焦点,两
焦点的距离叫双曲线的焦距。共性:
1、两者都是平面内动点到两定点的距离问题;
2、两者的定点都是焦点;
3、两者定点间的距离都是焦距。区别:
椭圆是距离之和;
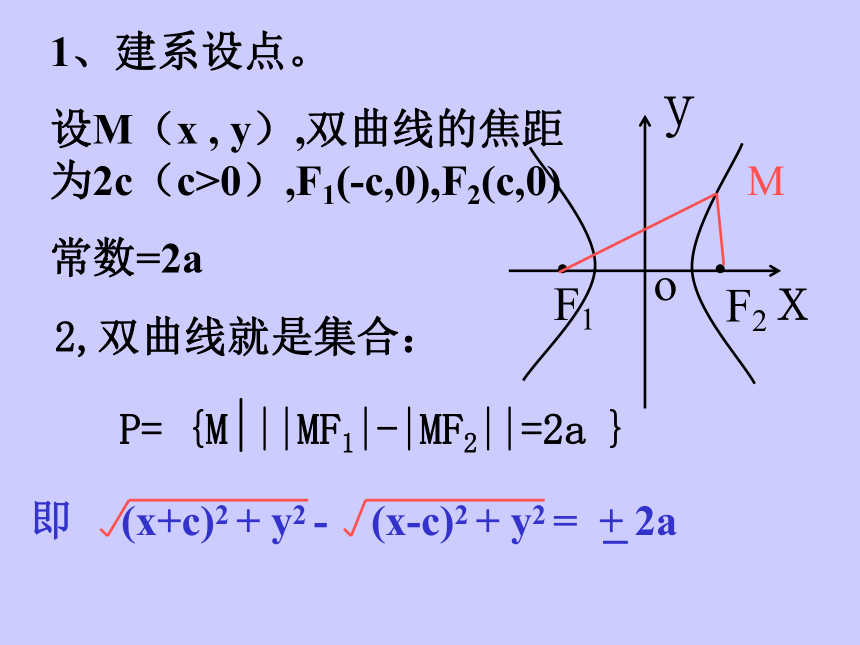
双曲线是距离之差的绝对值。求双曲线的标准方程1、建系设点。
设M(x , y),双曲线的焦距为2c(c>0),F1(-c,0),F2(c,0)
常数=2aF1F2M cx-a2=± a √(x-c)2+y2
(c2-a2) x2-a2y2=a2(c2-a2)
∵c>a,∴c2 >a2
令(c2-a2)=b2 (b>0)我们称这个方程为双曲线的标准方程焦点在y轴上的双曲线的标准方程是什么?想一想两种不同类型的双曲线方程只是x的平方项与y的平方项系数有着不同的符号。变1、焦点在x轴的双曲线时,求焦点坐标
例1、如果方程 表示双曲线,求m的范围解(m-1)(2-m)<0,∴m>2或m<1变2、焦点在x轴的椭圆时,求焦点坐标例2.已知双曲线的焦点为F1(-5,0),
F2(5,0)双曲线上一点到焦点的距
离差的绝对值等于6,求双曲线的标准方程。求标准方程的关键是什么?1、中心、焦点位置定性;
2、a、b 定量。位置、大小定标准方程X型:Y型:练习 1.求适合下列条件的双曲线的标准方程. (1)(2)焦点(0,-6),(0,6),经过点(2,-5). 2.已知方程 ,求它的焦点坐标. 3.已知方程 表示双曲线,求的取值范围.
例3,证明椭圆
与双曲线x2-15y2=15的焦点相同.变:椭圆与双曲线的一个交点为P,F1是椭圆的左焦点,求|PF1|.ABoA1x小结例题:
根据下列条件,求双曲线的标准方程:
1、过点 P ( 3 , )、Q ( , 5 ) 且焦点在坐标
轴上;
2、 c = ,经过点 (-5 , 2 ),焦点在 x 轴上;
3、与双曲线 的相同焦点,且经过
点 ( 3 , 2 )堂上练习
1.a=5,b=4且焦点在x轴上.
2.a=4,c=6且焦点在y轴上.
3.a=3,焦点坐标是(0,-5)和(0,5).课后作业:
P108习题8.3
第1题、第2题、第3题
2.椭圆的标准方程、焦点坐标是什么?y|MF1|+|MF2|=2a(2a>|F1F2|)a2=b2+c2
F ( ±c,0) F(0, ± c)
双曲线的定义平面内与两定点F1`F2的距离的差的绝对值等于常数(小于|F1F2 | )的点的轨迹叫做双曲线。
这两个定点叫做双曲线的焦点,
两焦点的距离叫做双曲线的焦距。 双曲线的一支
两条射线 1、平面内与两定点F1,F2的距离的差等于常数(小于 |F1F2 | )的点的轨迹是什么?2、若常数2a=0,轨迹是什么?
3、若常数2a= |F1F2|轨迹是什么?垂直平分线椭圆:平面内与两定点 F 1、F2的距离之和等
于常数( 大于 | F 1F2 | ) 的点的轨迹叫做椭圆。
这两定点叫做椭圆的焦点,两焦点的距离叫椭
圆的焦距。双曲线:平面内与两定点 F 1、F2的距离的差
的绝对值等于常数( 小于 | F 1F2 | ) 的点的轨迹
叫做双曲线。这两定点叫做双曲线的焦点,两
焦点的距离叫双曲线的焦距。共性:
1、两者都是平面内动点到两定点的距离问题;
2、两者的定点都是焦点;
3、两者定点间的距离都是焦距。区别:
椭圆是距离之和;
双曲线是距离之差的绝对值。求双曲线的标准方程1、建系设点。
设M(x , y),双曲线的焦距为2c(c>0),F1(-c,0),F2(c,0)
常数=2aF1F2M cx-a2=± a √(x-c)2+y2
(c2-a2) x2-a2y2=a2(c2-a2)
∵c>a,∴c2 >a2
令(c2-a2)=b2 (b>0)我们称这个方程为双曲线的标准方程焦点在y轴上的双曲线的标准方程是什么?想一想两种不同类型的双曲线方程只是x的平方项与y的平方项系数有着不同的符号。变1、焦点在x轴的双曲线时,求焦点坐标
例1、如果方程 表示双曲线,求m的范围解(m-1)(2-m)<0,∴m>2或m<1变2、焦点在x轴的椭圆时,求焦点坐标例2.已知双曲线的焦点为F1(-5,0),
F2(5,0)双曲线上一点到焦点的距
离差的绝对值等于6,求双曲线的标准方程。求标准方程的关键是什么?1、中心、焦点位置定性;
2、a、b 定量。位置、大小定标准方程X型:Y型:练习 1.求适合下列条件的双曲线的标准方程. (1)(2)焦点(0,-6),(0,6),经过点(2,-5). 2.已知方程 ,求它的焦点坐标. 3.已知方程 表示双曲线,求的取值范围.
例3,证明椭圆
与双曲线x2-15y2=15的焦点相同.变:椭圆与双曲线的一个交点为P,F1是椭圆的左焦点,求|PF1|.ABoA1x小结例题:
根据下列条件,求双曲线的标准方程:
1、过点 P ( 3 , )、Q ( , 5 ) 且焦点在坐标
轴上;
2、 c = ,经过点 (-5 , 2 ),焦点在 x 轴上;
3、与双曲线 的相同焦点,且经过
点 ( 3 , 2 )堂上练习
1.a=5,b=4且焦点在x轴上.
2.a=4,c=6且焦点在y轴上.
3.a=3,焦点坐标是(0,-5)和(0,5).课后作业:
P108习题8.3
第1题、第2题、第3题
