命题、定理
图片预览








文档简介
课件26张PPT。5.3.2 命题、定理甲同学:
1、我是中国人;
2、我的球鞋是新的;
3、熊猫没有翅膀;
4、对顶角相等;乙同学:
1、今天下雨吗?
2、你吃早饭了吗?
3、画一个60度的角;
4、直线AB与CD平行吗?设问2:这两组语句有何区别吗?设问1:这一组语句有什么共同特点吗?下列四个语句有什么共同点?(1)如果两条直线都与第三条直线平行,那么这两条直线也互相平行;
(2)两条平行线被第三条直线所截,同旁内角互补;
(3)对顶角相等;
(4)等式两边加同一个数,结果仍是等式.这些语句都是对某一件事情作出“是”或“不是”的判断.1.命题的定义:判断一件事情的语句,叫做命题.观察与发现:1、下列语句是命题的是( )
A、你去哪里?
B、画一个圆
C、圆是一个美丽的图形呀!
D、相等的角是内错角疑问句、祈使句、感叹句等不是命题。
D巩固概念:2、下列语句不是命题的是( )
A、延长线段AB
B、自然数是整数
C、两个锐角的和是钝角
D、同角的补角相等疑问句、祈使句、感叹句等不是命题。
A巩固概念:3、下列语句中,不是命题的句子是( )
A、两点之间线段最短;
B、篮球是圆的;
C、同位角相等;
D、连接A、B两点。4、给出下列语句: ①连接AB并延长到C;②两条直线相交,有几个交点?③两个锐角互余;④内错角相等,两直线平行;⑤求线段的长度;其中是命题的是( )
A、③④⑤ B、④ C、④⑤ D、③④注:命题作出的判断可能是正确的,也可以是错误的。巩固概念:DD2)两条直线相交,有且只有一个交点( )4)对顶角相等( )6)取线段AB的中点C;( )1)长度相等的两条线段是相等的线段吗?( )7)画两条相等的线段( )5 、判断下列语句是不是命题?是用“√”,
不是用“× 表示。3)不相等的两个角不是对顶角( )5)相等的两个角是对顶角( )×√××√√√探求新知: 观察下列语句,并判断是不是命题。
(1)如果两个角相等,那么它们是对顶角;
(2)如果a>b,b>c,那么a>c;
(3)如果等式的两边加上同一个数,那么结果仍是等式;
(4)如果两条平行直线被第三条直线所截,那么同旁内角互补;设问:这些命题都有哪些共同特点呢?1、上面的四个命题都是”如果……,那么……“的形式。
2、由两部分组成,一部分是已知事项,另一部分是由已知事项推出的事项。题设: 是已知事项;
结论: 是由已知事项推出的事项
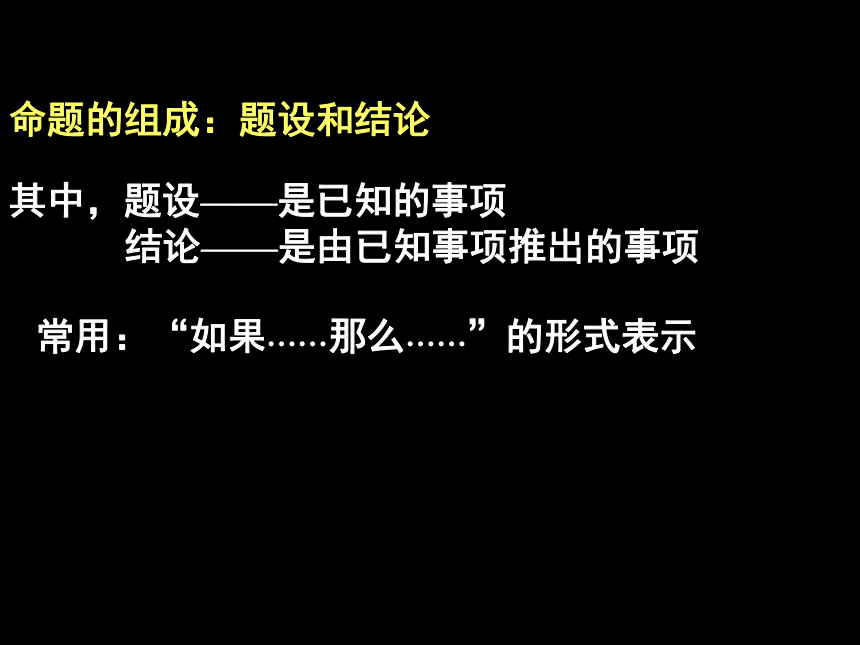
一般地,命题由题设和结论两部分组成。命题的组成:题设和结论其中,题设——是已知的事项
结论——是由已知事项推出的事项常用:“如果……那么……”的形式表示命题如果……那么……题 设结 论1.如果同位角相等,那么两直线平行.
2.如果两直线平行,那么内错角相等.
3.如果a∥b,b ∥c,那么a ∥c.
4.如果两个角不相等,那么这两个角不是对顶角. 指出下面命题的题设和结论:注:对于一个命题,如果题设与结论不明显时,我们应该先将命题改写”如果……,那么……“的形式。 “如果”开始的部分是题设, “那么”开始的部分是结论。如:对顶角相等题设结论如果两个角是对顶角,那么这两个角相等题设结论例1、指下面的命题的题设和结论,并改写成“如果……那么……”的形式。
1、两直线平行,同旁内角互补。
2、邻补角是互补的角。
3、小于直角的角是锐角。
4、等角的补角相等。
5、平行于同一条直线的两条直线平行。练习:指出下列命题的题设和结论,并改写
成“如果……那么……” 的形式.
(1)两直线平行,同位角相等;
(2)等角的余角相等
(3) 相等的角是对顶角
(4)三个内角都等于60°的三角形是
等边三角形
(5)垂直于同一条直线的两条直线平行1、如果a>0,b>0,那么a+b>0
2、如果a>0,b>0,那么a+b<0观察以下两个命题,并说说这两个命题有什么相同和不同的地方?观察与发现: 如果题设成立,那么结论一定成立,
这样的一些命题叫做真命题. 如果题设成立时,不能保证结论一定
成立,它就是错误的命题,像这样的命题
叫做假命题.真命题与假命题例2、哪些是真命题,哪些是假命题?
1)一个角的补角大于这个角
2)相等的两个角是对顶角
3)两点可以确定一条直线
4)若A=B,则2A=2B
5)锐角和钝角互为补角
6)两点之间线段最短
7)同角的余角相等(假命题)(假命题)(真命题)(真命题)(假命题)(真命题)(真命题)(9)如果两个角互补,那么它们是邻补角 .
(10)如果一个数能被2整除,那么它也能被4整除.注:判断一个命题是假命题时要举反例8)同位角相等(假命题)(假命题)(假命题)判断一个命题是假命题的方法:“举反例”例如:
证明:“一个锐角与一个钝角的和等于一个平角”是假命题。只需举一反例: 锐角30°,钝角120°,它们的和就不等于180°,所以:这个命题是假命题公理公理:人们在长期实践中总结出来的,并把它们作为判断其他命题真假的原始依据的命题。(它们是不需要证明的基本事实)定理定理:用逻辑推理的方法判断它们是正确的,并且可以进一步作为判断其他命题真假的依据。这样得到的真命题叫做定理。
(它们是需要证明其正确性后才能用)过两点有且只有一条直线.2) 线段公理:两点之间,线段最短.4) 平行线判定公理:同位角相等,两直线平行.5) 平行线性质公理:两直线平行,同位角相等.1) 直线公理:3) 平行公理:经过直线外一点,有且只有一条
直线与已知直线平行.1、下列语句中,不是命题的句子是 ( )
A 过一点做已知直线的垂线;
B 两点确定一条直线;
C 钝角小于90O;
D 凡平角都相等。2、命题是 一件事情的句子,命题都是由 和 两部分组成。3、命题“若a≠b,则a2≠b2”的题设是 ,结论是 。达标小测验4、指出下列命题的题设和结论,并说明其真假性.
(1)如果AB⊥CD,垂足是O,那么∠AOC=90°.
(2)两直线平行, 同位角相等 .
(3)如果两个角互补,那么它们是邻补角 .
(4)如果一个数能被2整除,那么它也能被4整除.解:(1) 题设是“AB⊥CD,垂足是O”,结论是“∠AOC=90°”. (2) 题设是“两直线平行”,结论是“同位角相等 ”. (3) 题设是“两个角互补”,结论是“它们是邻补角 ”. (4) 题设是“一个数能被2整除”,结论是“它也能被4整除”.
(1)命题“同角的余角相等”的题设是( )
A同角 B同角的余角 C余角相等 D等角的余角相等
(2)命题“等角的补角相等”中的“补角”是( )
(A)题设部分 (B)同属于题设和结论部分
(C)结论部分 (D)既不属题设也不属结论
(3)“两负数之积为正数”的题设是____,结论是____;
(4)把“在同一平面内,垂直于同一条直线的两直线互相平行”改写成“如果______,那么_____”的形式.拓展延伸1)每个命题都是由题设、结论两部分组成.1.定义:判断一件事情的语句.2)命题常写成“如果······那么······”的形式.2)假命题:错误的命题.1)真命题:正确的命题;小结:2.构成:3.分类:
1、我是中国人;
2、我的球鞋是新的;
3、熊猫没有翅膀;
4、对顶角相等;乙同学:
1、今天下雨吗?
2、你吃早饭了吗?
3、画一个60度的角;
4、直线AB与CD平行吗?设问2:这两组语句有何区别吗?设问1:这一组语句有什么共同特点吗?下列四个语句有什么共同点?(1)如果两条直线都与第三条直线平行,那么这两条直线也互相平行;
(2)两条平行线被第三条直线所截,同旁内角互补;
(3)对顶角相等;
(4)等式两边加同一个数,结果仍是等式.这些语句都是对某一件事情作出“是”或“不是”的判断.1.命题的定义:判断一件事情的语句,叫做命题.观察与发现:1、下列语句是命题的是( )
A、你去哪里?
B、画一个圆
C、圆是一个美丽的图形呀!
D、相等的角是内错角疑问句、祈使句、感叹句等不是命题。
D巩固概念:2、下列语句不是命题的是( )
A、延长线段AB
B、自然数是整数
C、两个锐角的和是钝角
D、同角的补角相等疑问句、祈使句、感叹句等不是命题。
A巩固概念:3、下列语句中,不是命题的句子是( )
A、两点之间线段最短;
B、篮球是圆的;
C、同位角相等;
D、连接A、B两点。4、给出下列语句: ①连接AB并延长到C;②两条直线相交,有几个交点?③两个锐角互余;④内错角相等,两直线平行;⑤求线段的长度;其中是命题的是( )
A、③④⑤ B、④ C、④⑤ D、③④注:命题作出的判断可能是正确的,也可以是错误的。巩固概念:DD2)两条直线相交,有且只有一个交点( )4)对顶角相等( )6)取线段AB的中点C;( )1)长度相等的两条线段是相等的线段吗?( )7)画两条相等的线段( )5 、判断下列语句是不是命题?是用“√”,
不是用“× 表示。3)不相等的两个角不是对顶角( )5)相等的两个角是对顶角( )×√××√√√探求新知: 观察下列语句,并判断是不是命题。
(1)如果两个角相等,那么它们是对顶角;
(2)如果a>b,b>c,那么a>c;
(3)如果等式的两边加上同一个数,那么结果仍是等式;
(4)如果两条平行直线被第三条直线所截,那么同旁内角互补;设问:这些命题都有哪些共同特点呢?1、上面的四个命题都是”如果……,那么……“的形式。
2、由两部分组成,一部分是已知事项,另一部分是由已知事项推出的事项。题设: 是已知事项;
结论: 是由已知事项推出的事项
一般地,命题由题设和结论两部分组成。命题的组成:题设和结论其中,题设——是已知的事项
结论——是由已知事项推出的事项常用:“如果……那么……”的形式表示命题如果……那么……题 设结 论1.如果同位角相等,那么两直线平行.
2.如果两直线平行,那么内错角相等.
3.如果a∥b,b ∥c,那么a ∥c.
4.如果两个角不相等,那么这两个角不是对顶角. 指出下面命题的题设和结论:注:对于一个命题,如果题设与结论不明显时,我们应该先将命题改写”如果……,那么……“的形式。 “如果”开始的部分是题设, “那么”开始的部分是结论。如:对顶角相等题设结论如果两个角是对顶角,那么这两个角相等题设结论例1、指下面的命题的题设和结论,并改写成“如果……那么……”的形式。
1、两直线平行,同旁内角互补。
2、邻补角是互补的角。
3、小于直角的角是锐角。
4、等角的补角相等。
5、平行于同一条直线的两条直线平行。练习:指出下列命题的题设和结论,并改写
成“如果……那么……” 的形式.
(1)两直线平行,同位角相等;
(2)等角的余角相等
(3) 相等的角是对顶角
(4)三个内角都等于60°的三角形是
等边三角形
(5)垂直于同一条直线的两条直线平行1、如果a>0,b>0,那么a+b>0
2、如果a>0,b>0,那么a+b<0观察以下两个命题,并说说这两个命题有什么相同和不同的地方?观察与发现: 如果题设成立,那么结论一定成立,
这样的一些命题叫做真命题. 如果题设成立时,不能保证结论一定
成立,它就是错误的命题,像这样的命题
叫做假命题.真命题与假命题例2、哪些是真命题,哪些是假命题?
1)一个角的补角大于这个角
2)相等的两个角是对顶角
3)两点可以确定一条直线
4)若A=B,则2A=2B
5)锐角和钝角互为补角
6)两点之间线段最短
7)同角的余角相等(假命题)(假命题)(真命题)(真命题)(假命题)(真命题)(真命题)(9)如果两个角互补,那么它们是邻补角 .
(10)如果一个数能被2整除,那么它也能被4整除.注:判断一个命题是假命题时要举反例8)同位角相等(假命题)(假命题)(假命题)判断一个命题是假命题的方法:“举反例”例如:
证明:“一个锐角与一个钝角的和等于一个平角”是假命题。只需举一反例: 锐角30°,钝角120°,它们的和就不等于180°,所以:这个命题是假命题公理公理:人们在长期实践中总结出来的,并把它们作为判断其他命题真假的原始依据的命题。(它们是不需要证明的基本事实)定理定理:用逻辑推理的方法判断它们是正确的,并且可以进一步作为判断其他命题真假的依据。这样得到的真命题叫做定理。
(它们是需要证明其正确性后才能用)过两点有且只有一条直线.2) 线段公理:两点之间,线段最短.4) 平行线判定公理:同位角相等,两直线平行.5) 平行线性质公理:两直线平行,同位角相等.1) 直线公理:3) 平行公理:经过直线外一点,有且只有一条
直线与已知直线平行.1、下列语句中,不是命题的句子是 ( )
A 过一点做已知直线的垂线;
B 两点确定一条直线;
C 钝角小于90O;
D 凡平角都相等。2、命题是 一件事情的句子,命题都是由 和 两部分组成。3、命题“若a≠b,则a2≠b2”的题设是 ,结论是 。达标小测验4、指出下列命题的题设和结论,并说明其真假性.
(1)如果AB⊥CD,垂足是O,那么∠AOC=90°.
(2)两直线平行, 同位角相等 .
(3)如果两个角互补,那么它们是邻补角 .
(4)如果一个数能被2整除,那么它也能被4整除.解:(1) 题设是“AB⊥CD,垂足是O”,结论是“∠AOC=90°”. (2) 题设是“两直线平行”,结论是“同位角相等 ”. (3) 题设是“两个角互补”,结论是“它们是邻补角 ”. (4) 题设是“一个数能被2整除”,结论是“它也能被4整除”.
(1)命题“同角的余角相等”的题设是( )
A同角 B同角的余角 C余角相等 D等角的余角相等
(2)命题“等角的补角相等”中的“补角”是( )
(A)题设部分 (B)同属于题设和结论部分
(C)结论部分 (D)既不属题设也不属结论
(3)“两负数之积为正数”的题设是____,结论是____;
(4)把“在同一平面内,垂直于同一条直线的两直线互相平行”改写成“如果______,那么_____”的形式.拓展延伸1)每个命题都是由题设、结论两部分组成.1.定义:判断一件事情的语句.2)命题常写成“如果······那么······”的形式.2)假命题:错误的命题.1)真命题:正确的命题;小结:2.构成:3.分类:
