整数指数幂
图片预览





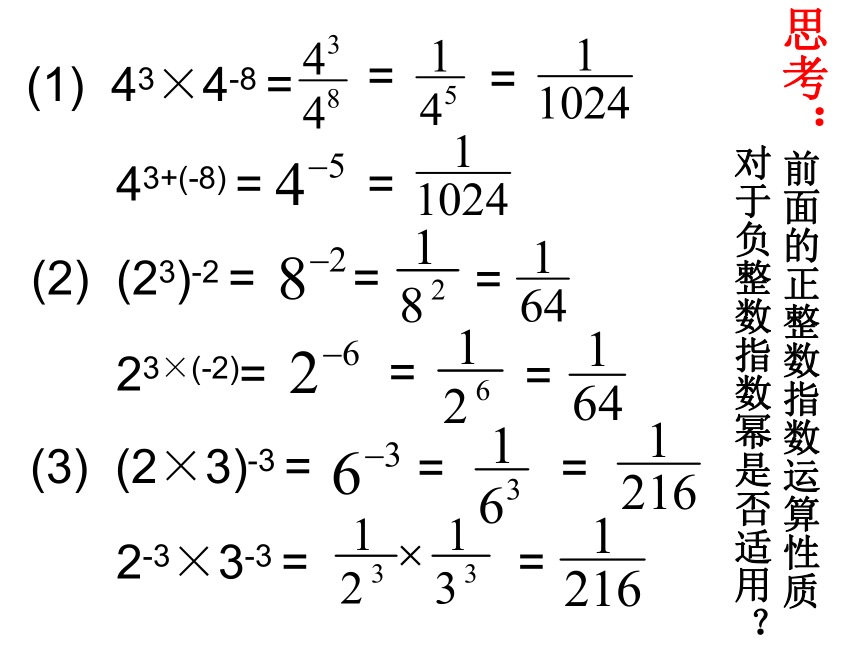

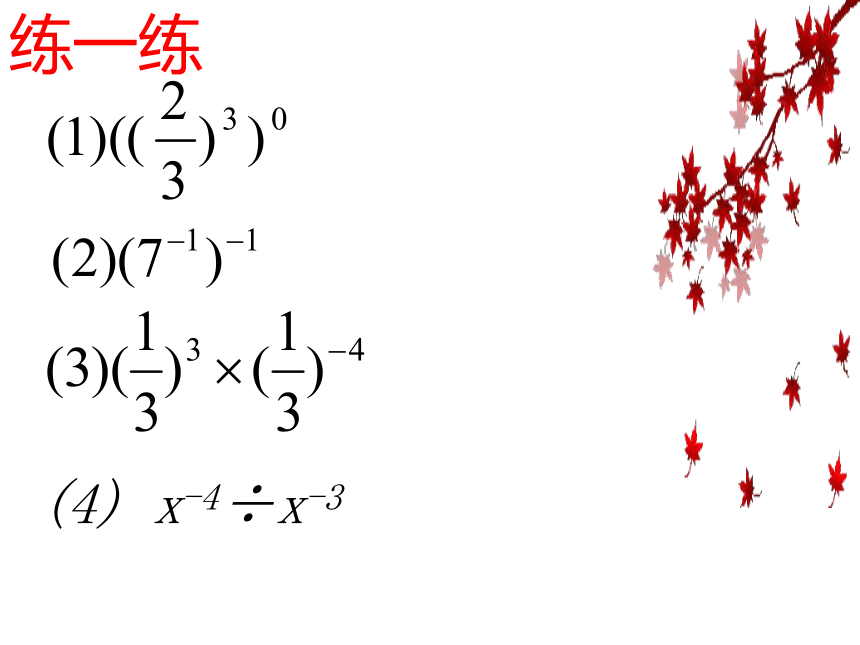
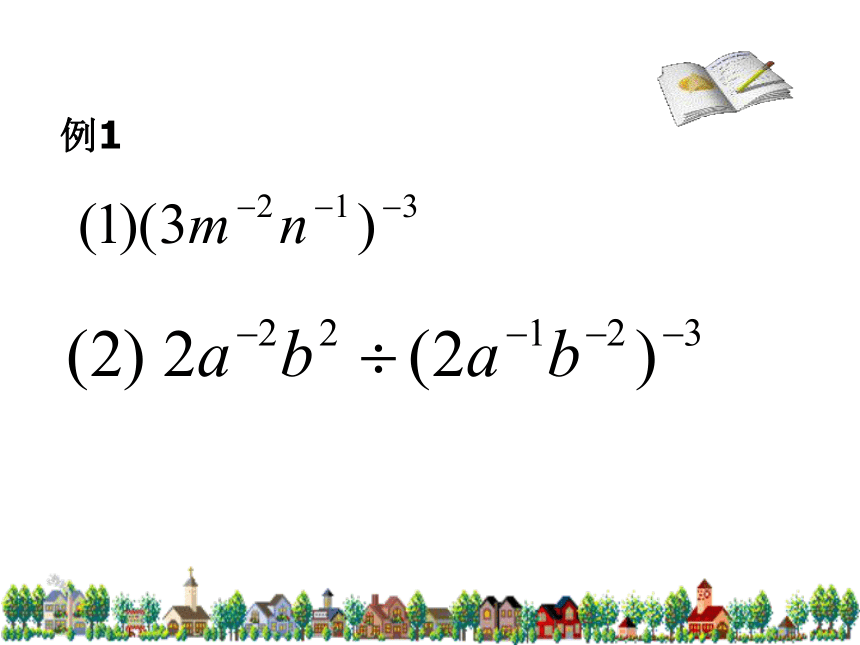
文档简介
课件23张PPT。整数指数幂 (a?b)n= an?bn 正整数指数幂的运算法则m,n为正整数am?an=am+n(am)n=am?n当a≠0时,a0=1。(0指数幂的运算)am÷an=am-n (a≠0 m、n为正整数且m>n)a5÷a3=a2a3÷a5=?a3÷a5=a3-5=a-2a3÷a5==思考:在 中,当n是负整数时,
表示什么意义?n是正整数时, a-n属于分式。并且(a≠0)例如:引入负整数指数幂后,指数的取值范围就扩大到全体整数。 (n是正整数)(n=0)(n是负整数)1例题计算:(1) 43×4-8 = 43+(-8) =(2) (23)-2 =23×(-2)=(3) (2×3)-3 =2-3×3-3 ===========思考:前面的正整数指数运算性质
对于负整数指数幂是否适用?整数指数幂有以下运算性质:(1)am·an=am+n (a≠0)
(2)(am)n=amn (a≠0)
(3)(ab)n=anbn (a,b≠0)
(4)am÷an=am-n (a≠0)
(5) (b≠0)
当a≠0时,a0=1。(6)a-3·a-9=
(a-3)2=
(ab)-3=
a-3÷a-5=练一练(4) x-4÷x-3例1练习(1) (-6x-2)2+2x0
(2)(3x-1)-2 ÷(-2x)-3
(3)--3用一用(4)课堂达标测试基础题:1.计算:
(a+b)m+1·(a+b)n-1; (2) (-a2b)2·(-a2b3)3÷(-ab4)5
(3) (x3)2÷(x2)4·x0
(4) (-1.8x4y2z3) ÷(-0.2x2y4z) ÷(-1/3xyz)提高题:2.已知 ,求a51÷a8的值;3.计算:xn+2·xn-2÷(x2)3n-3;4.已知:10m=5,10n=4,求102m-3n.?概念:科学记数法:绝对值大于10的数记成a×10n的形式,其中
1≤ <10,n是正整数。例如,864000可以写成8.64×105. 用小数表示下列各数类似地,我们可以利用10的负整数次幂,
用科学记数法表示一些绝对值较小的数,
即将它们表示成a×10- n的形式,其中n是
正整数,1≤∣a∣<10.0.01=0.00000001=0.1=0.00001=1 × 10-11 × 10-21 × 10-51 × 10-8例题1:用科学记数法表示下列各数0.000611= -0.00105=6.11 × 10-4 -1.05 × 10-3思考:当绝对值较小的数用科学记数法表示为a ×10-n时,a,n有什么特点?a的取值一样为1≤︱a︱<10;n是正整数,n等于原数中左边第一个不为0的数字前面所有的0的个数。(包括小数点前面的0)0.0‥‥‥01=1 × 10-nn个06.075×10-4- 3.099×10-1- 6.07×10-3- 1.009874×1061.06×105并指出结果的精确度与有效数字。用a ×10n 表示的数,其有效数字由a来确定,其精确度由原数来确定。分析:把a×10-n还原成原数时,只需把a的小数点
点向左移动n位。 (1)7.213×10-5=(2)-1.5×10-4=例3:把下列科学记数法还原。自学课本例114、计算:(结果用科学记数法表示)1、比较大小:
(1)3.01×10-4--------------9.5×10-3
<(2)3.01×10-4-----------3.10×10-4<①用科学记数法表示,并把结果保留两位有效数字:
(1)0.000 03; (2)-0.000 00647;
(3)0.000 0314; (4)2013 000.
用科学记数法填空:
(1)1微秒=_________秒;
(2)1毫克=_________克=_________千克;
(3)1微米=_________厘米=_________ 米;
(4)1纳米=_________微米=_________米;
(5)1平方厘米=_________平方米;
(6)1毫升= _________ 升=_________立方米.生活小常识1×10-61×10-61×10-31×10-61×10-41×10-41×10-61×10-31×10-91×10-3
表示什么意义?n是正整数时, a-n属于分式。并且(a≠0)例如:引入负整数指数幂后,指数的取值范围就扩大到全体整数。 (n是正整数)(n=0)(n是负整数)1例题计算:(1) 43×4-8 = 43+(-8) =(2) (23)-2 =23×(-2)=(3) (2×3)-3 =2-3×3-3 ===========思考:前面的正整数指数运算性质
对于负整数指数幂是否适用?整数指数幂有以下运算性质:(1)am·an=am+n (a≠0)
(2)(am)n=amn (a≠0)
(3)(ab)n=anbn (a,b≠0)
(4)am÷an=am-n (a≠0)
(5) (b≠0)
当a≠0时,a0=1。(6)a-3·a-9=
(a-3)2=
(ab)-3=
a-3÷a-5=练一练(4) x-4÷x-3例1练习(1) (-6x-2)2+2x0
(2)(3x-1)-2 ÷(-2x)-3
(3)--3用一用(4)课堂达标测试基础题:1.计算:
(a+b)m+1·(a+b)n-1; (2) (-a2b)2·(-a2b3)3÷(-ab4)5
(3) (x3)2÷(x2)4·x0
(4) (-1.8x4y2z3) ÷(-0.2x2y4z) ÷(-1/3xyz)提高题:2.已知 ,求a51÷a8的值;3.计算:xn+2·xn-2÷(x2)3n-3;4.已知:10m=5,10n=4,求102m-3n.?概念:科学记数法:绝对值大于10的数记成a×10n的形式,其中
1≤ <10,n是正整数。例如,864000可以写成8.64×105. 用小数表示下列各数类似地,我们可以利用10的负整数次幂,
用科学记数法表示一些绝对值较小的数,
即将它们表示成a×10- n的形式,其中n是
正整数,1≤∣a∣<10.0.01=0.00000001=0.1=0.00001=1 × 10-11 × 10-21 × 10-51 × 10-8例题1:用科学记数法表示下列各数0.000611= -0.00105=6.11 × 10-4 -1.05 × 10-3思考:当绝对值较小的数用科学记数法表示为a ×10-n时,a,n有什么特点?a的取值一样为1≤︱a︱<10;n是正整数,n等于原数中左边第一个不为0的数字前面所有的0的个数。(包括小数点前面的0)0.0‥‥‥01=1 × 10-nn个06.075×10-4- 3.099×10-1- 6.07×10-3- 1.009874×1061.06×105并指出结果的精确度与有效数字。用a ×10n 表示的数,其有效数字由a来确定,其精确度由原数来确定。分析:把a×10-n还原成原数时,只需把a的小数点
点向左移动n位。 (1)7.213×10-5=(2)-1.5×10-4=例3:把下列科学记数法还原。自学课本例114、计算:(结果用科学记数法表示)1、比较大小:
(1)3.01×10-4--------------9.5×10-3
<(2)3.01×10-4-----------3.10×10-4<①用科学记数法表示,并把结果保留两位有效数字:
(1)0.000 03; (2)-0.000 00647;
(3)0.000 0314; (4)2013 000.
用科学记数法填空:
(1)1微秒=_________秒;
(2)1毫克=_________克=_________千克;
(3)1微米=_________厘米=_________ 米;
(4)1纳米=_________微米=_________米;
(5)1平方厘米=_________平方米;
(6)1毫升= _________ 升=_________立方米.生活小常识1×10-61×10-61×10-31×10-61×10-41×10-41×10-61×10-31×10-91×10-3
