8.3一元一次不等式组的应用(第2课时)课件
文档属性
| 名称 | 8.3一元一次不等式组的应用(第2课时)课件 |  | |
| 格式 | rar | ||
| 文件大小 | 317.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-03-07 19:21:00 | ||
图片预览





文档简介
课件13张PPT。8.3一元一次不等式组的应用回顾交流1.什么叫一元一次不等式组?
怎样解一元一次不等式组?
2.试一试:答:_-6____ 已知不等式组 的解
集为-1<x<1,则(a+1)(b-1)的值为多少? 若 ︱ x ︱=2,则x= 若︱ x ︱<2,则x若︱4 x ︱ <8, 则x若︱4 x-3 ︱ <2,则x±2-2 < x < 2-2 < x < 2由题意得:-2 < 4x -3< 24x-3 < 24x-3>-2合作探索2、一群女生住若干间宿舍,
每间住4人,剩19人无房住;每
间住6人,有一间宿舍住不满,
(1)设有x间宿舍,请写出x应满
足的不等式组;
(2)可能有多少间宿舍,多少名
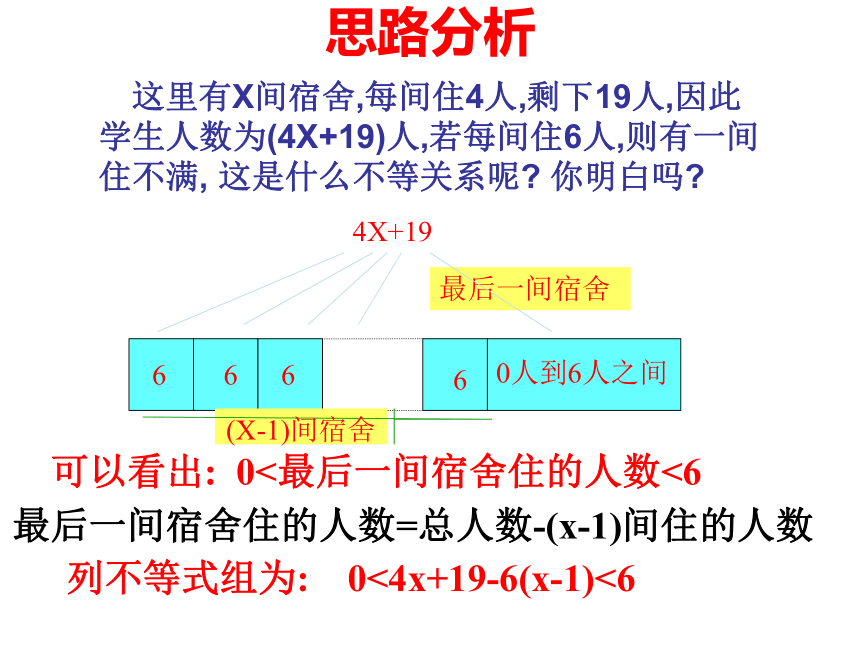
学生? 思路分析 这里有X间宿舍,每间住4人,剩下19人,因此学生人数为(4X+19)人,若每间住6人,则有一间住不满, 这是什么不等关系呢? 你明白吗? 6 664X+190人到6人之间最后一间宿舍6(X-1)间宿舍列不等式组为: 0<4x+19-6(x-1)<6可以看出: 0<最后一间宿舍住的人数<6最后一间宿舍住的人数=总人数-(x-1)间住的人数解: 设有x间宿舍,根据题意得不等式组: 0<4x+19-6(x-1)<6即: 4x+19-6(x-1)>0
4x+19-6(x-1)<6
解得: 18.5因为x是整数,所以x=10,11,12.
因此可能有10间宿舍,59名学生或11间宿舍,63名学生或12间宿舍,67名学生.实践应用,合作探索例2: 某工厂现有甲种原料360kg,乙种原料290kg,计划利用这两种原料生产A,B两种产品共50件,已知生产一件A产品需要甲原料9kg,乙原料3kg,生产一件B产品需要甲原料4kg,乙原料10kg,
(1)设生产X件A种产品,写出X应满足的不等式组
(2)有哪几种符合的生产方案?
(3)若生产一件A产品可获利700元,生产一件B产品可获利1200元,那么采用哪种生产方案可使生产A、B两种产品的总获利最大?最大利润是多少?思路分析:
(1)本题的不等关系是:
生产A、B两种产品所需的甲种原料≤360
生产A、B两种产品所需的乙种原料≤290(2) 列表看各量的关系所以,列不等式组为:解得:30≤X≤32所以,可有三种生产方案:A种30件,B种20件;A种31件,B种19件;A种32件,B种18件。因为x为正整数,所以,X的可能取值为30,31,321、有堆苹果分给一组小朋友,如果每人5个,还有18个多余,如果每人7个,则还有一位小朋友分不到7个,求苹果的个数和小朋友的人数。解:设小朋友人数为x人,则苹果数为(5x+18)个,根据题意得:解得:9
怎样解一元一次不等式组?
2.试一试:答:_-6____ 已知不等式组 的解
集为-1<x<1,则(a+1)(b-1)的值为多少? 若 ︱ x ︱=2,则x= 若︱ x ︱<2,则x若︱4 x ︱ <8, 则x若︱4 x-3 ︱ <2,则x±2-2 < x < 2-2 < x < 2由题意得:-2 < 4x -3< 24x-3 < 24x-3>-2合作探索2、一群女生住若干间宿舍,
每间住4人,剩19人无房住;每
间住6人,有一间宿舍住不满,
(1)设有x间宿舍,请写出x应满
足的不等式组;
(2)可能有多少间宿舍,多少名
学生? 思路分析 这里有X间宿舍,每间住4人,剩下19人,因此学生人数为(4X+19)人,若每间住6人,则有一间住不满, 这是什么不等关系呢? 你明白吗? 6 664X+190人到6人之间最后一间宿舍6(X-1)间宿舍列不等式组为: 0<4x+19-6(x-1)<6可以看出: 0<最后一间宿舍住的人数<6最后一间宿舍住的人数=总人数-(x-1)间住的人数解: 设有x间宿舍,根据题意得不等式组: 0<4x+19-6(x-1)<6即: 4x+19-6(x-1)>0
4x+19-6(x-1)<6
解得: 18.5
因此可能有10间宿舍,59名学生或11间宿舍,63名学生或12间宿舍,67名学生.实践应用,合作探索例2: 某工厂现有甲种原料360kg,乙种原料290kg,计划利用这两种原料生产A,B两种产品共50件,已知生产一件A产品需要甲原料9kg,乙原料3kg,生产一件B产品需要甲原料4kg,乙原料10kg,
(1)设生产X件A种产品,写出X应满足的不等式组
(2)有哪几种符合的生产方案?
(3)若生产一件A产品可获利700元,生产一件B产品可获利1200元,那么采用哪种生产方案可使生产A、B两种产品的总获利最大?最大利润是多少?思路分析:
(1)本题的不等关系是:
生产A、B两种产品所需的甲种原料≤360
生产A、B两种产品所需的乙种原料≤290(2) 列表看各量的关系所以,列不等式组为:解得:30≤X≤32所以,可有三种生产方案:A种30件,B种20件;A种31件,B种19件;A种32件,B种18件。因为x为正整数,所以,X的可能取值为30,31,321、有堆苹果分给一组小朋友,如果每人5个,还有18个多余,如果每人7个,则还有一位小朋友分不到7个,求苹果的个数和小朋友的人数。解:设小朋友人数为x人,则苹果数为(5x+18)个,根据题意得:解得:9
