必修1 第二章 函数 2.1.3 函数的单调性 教案
文档属性
| 名称 | 必修1 第二章 函数 2.1.3 函数的单调性 教案 |

|
|
| 格式 | rar | ||
| 文件大小 | 161.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-03-04 00:00:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
第二章 函数
2.1.3 函数的单调性
本节教材分析
一 三维目标
1知识与能力目标
(1) 理解函数的单调性及其几何意义。
(2) 学会运用函数图象理解和研究函数的性质.。
(3) 理解增区间、减区间等概念,掌握增(减)函数的证明和判别。
2 过程与方法目标
(1)逐步借助图像、表格、自然语言和数学符号语言,建立增(减)函数的概念。
(2)学生利用定义证明单调性,进一步加强逻辑推理能力及判断推理能力的培养
(3)培养学生利用数学语言对概念进行概括的能力。
3情感态度与价值观目标
(1) 通过本节课的教学,启发学生养成细心观察,认真分析,严谨论证的良好习惯.
(2) 通过问题链的引入,激发学生学习数学的兴趣;学生通过积极参与教学活动,获得成功的体验,锻炼克服困难的意志,建立学习的信心。
二 教学重点
函数单调性的概念和判断。
三 教学难点
利用函数单调性的定义判断具体函数的单调性。
四 教学建议
函数的单调性是函数的一个重要性质,在讲解函数单调性的概念时要结合图形进行分析说明,是抽象的概念直观化,加深概念的理解。同时也要注意培养学生应用图形解决问题的能力。
新课导入设计
导入一:分别画y=2x,y=-2x和y= +1的函数图像,引导学生观察图像的升降变化,体会不同函数在不同区间上的变化差异,从而导入新课。
导入二:列举生活中的例子 比如
(1)近六届世界杯进球数如下表: 画成折线图:
年份 进球数
1990 115
1994 137
1998 171
2002 161
2006 147
2010 145
问题1:随着年份的不同,进球数有什么变化?进球数的变化和图象的变化有什么联系?
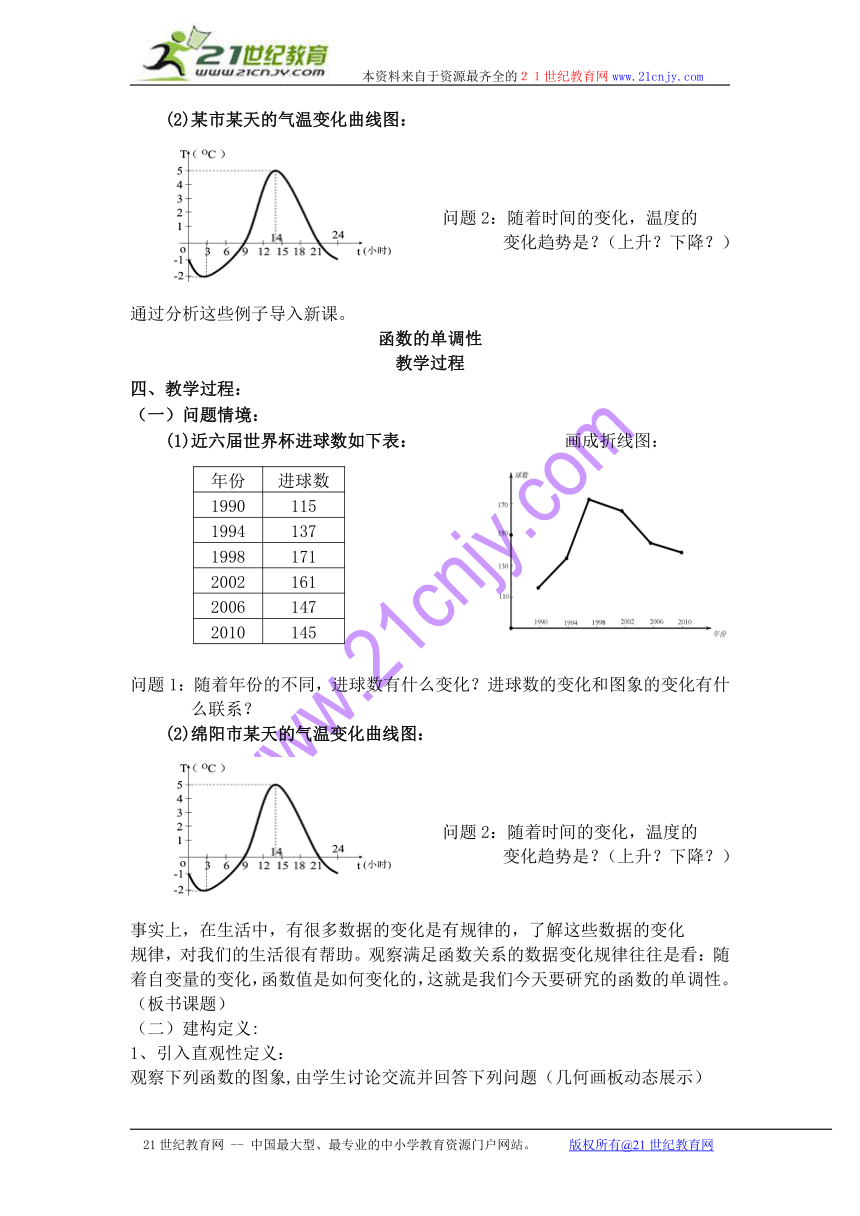
(2)某市某天的气温变化曲线图:
问题2:随着时间的变化,温度的
变化趋势是?(上升?下降?)
通过分析这些例子导入新课。
函数的单调性
教学过程
四、教学过程:
(一)问题情境:
(1)近六届世界杯进球数如下表: 画成折线图:
年份 进球数
1990 115
1994 137
1998 171
2002 161
2006 147
2010 145
问题1:随着年份的不同,进球数有什么变化?进球数的变化和图象的变化有什么联系?
(2)绵阳市某天的气温变化曲线图:
问题2:随着时间的变化,温度的
变化趋势是?(上升?下降?)
事实上,在生活中,有很多数据的变化是有规律的,了解这些数据的变化
规律,对我们的生活很有帮助。观察满足函数关系的数据变化规律往往是看:随着自变量的变化,函数值是如何变化的,这就是我们今天要研究的函数的单调性。
(板书课题)
(二)建构定义:
1、引入直观性定义:
观察下列函数的图象,由学生讨论交流并回答下列问题(几何画板动态展示)
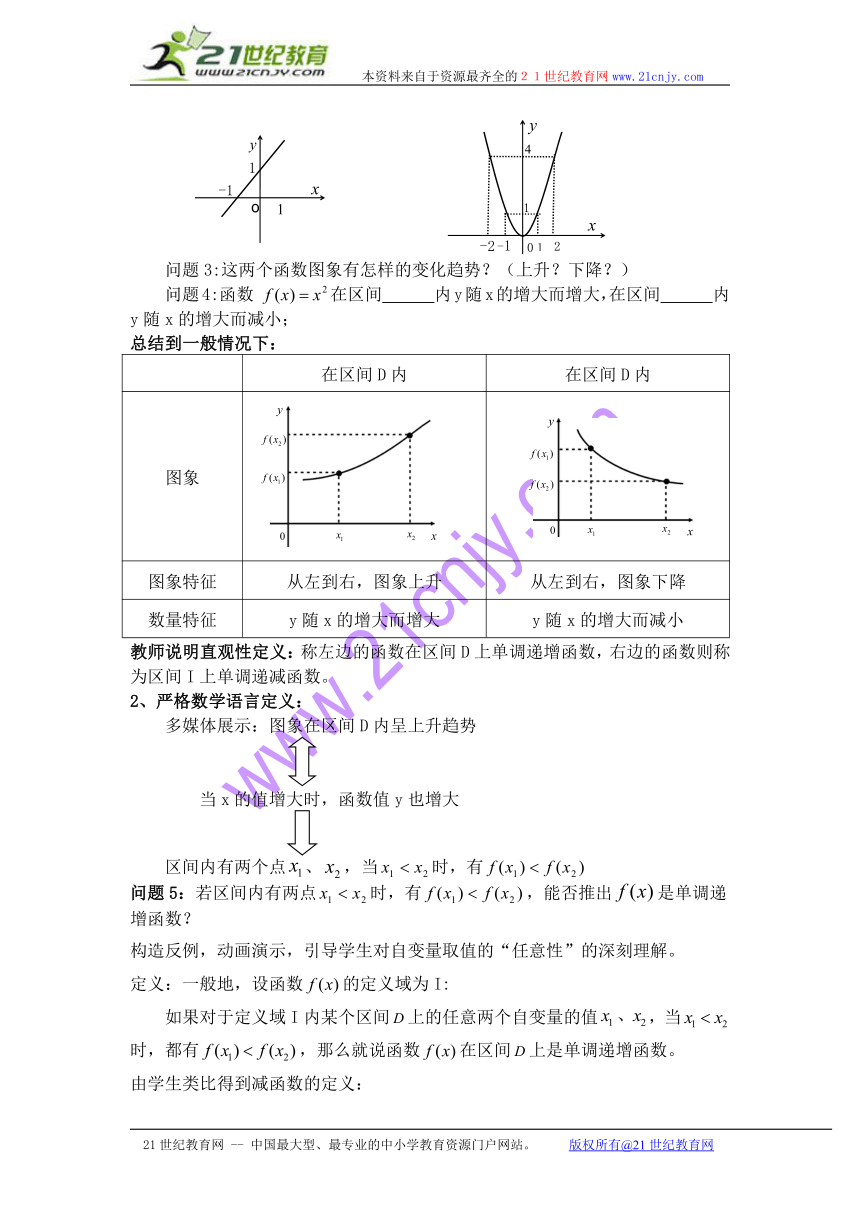
问题3:这两个函数图象有怎样的变化趋势?(上升?下降?)
问题4:函数在区间 内y随x的增大而增大,在区间 内
y随x的增大而减小;
总结到一般情况下:
在区间D内 在区间D内
图象
图象特征 从左到右,图象上升 从左到右,图象下降
数量特征 y随x的增大而增大 y随x的增大而减小
教师说明直观性定义:称左边的函数在区间D上单调递增函数,右边的函数则称为区间I上单调递减函数。
2、严格数学语言定义:
多媒体展示:图象在区间D内呈上升趋势
当x的值增大时,函数值y也增大
区间内有两个点、,当时,有
问题5:若区间内有两点时,有,能否推出是单调递
增函数?
构造反例,动画演示,引导学生对自变量取值的“任意性”的深刻理解。
定义:一般地,设函数的定义域为I:
如果对于定义域I内某个区间上的任意两个自变量的值,当时,都有,那么就说函数在区间上是单调递增函数。
由学生类比得到减函数的定义:
如果对于定义域I内某个区间上的任意两个自变量的值,当时,都有,那么就说函数在区间上是单调递减函数。
注:
(1)三大特征:①属于同一区间;②任意性;③有大小:通常规定;
(2)相对于定义域,函数的单调性可以是函数的局部性质。
举例:在上是单调增函数,但在整个定义域上不是增(减)函数。
(三)定义应用:
例1、下图是定义在[-5,5]上的函数的图象,根据图象说出函数的单调区间,以及在每一单调区间上,是增函数还是减函数。
分析:动画演示,帮助学生理解。
解:的单调区间有[-5,-2),[-2,1),[1,3),[3,5]。
其中在[-5,-2),[1,3)上是减函数;
在[-2,1), [3,5)上是增函数。
强调单调区间的写法:
问题6:可否写成[-5,-2)U[-2,1)?
问题7:写成[-5,-2)还是写成[-5,-2]?
多媒体展示构造反例说明:
(1)单调区间一般不能求并集;
(2)当端点满足单调性定义时,可开可闭。
例2、试判断函数 在区间(0,+∞)上是增函数还是减函数?并给予证明。
分析:问1:除了图象法判定函数单调性还有什么方法?
2:如何用定义法判定函数单调性?
3:用定义判定函数单调性的关键是什么?(提示如何比较3和2的大小,从而引入作差法)
证明:函数 在(0,+∞)上是增函数
设 是(0,+∞)上的任意两个值,且,
则
又,故,
则,即:
因此,函数 在(0,+∞)上是增函数。
总结定义法证明函数单调性的步骤:
1、取值:设任意属于给定区间,且;
2、作差变形:变形的常用方法:因式分解、配方、有理化等;
3、定号:确定的正负号;
4、下结论:由定义得出函数的单调性。
思考题:
在上面证明中,你能理解的任意性的意义吗?
解答:有了“任意性”在区间内不管取哪两个值,其证明过程都是一样的。
四、课堂练习:
(1)课本P65页1,
(2)证明:函数在上是减函数。(动画演示帮助理解)
课堂思考:
函数
单调区间
单调性
课后思考:
函数在R上单调递增,那么,的符号有什么规律?若单调递减,又该如何
五、回顾小结:
1、函数单调性的定义;
2、判定函数单调性:
(1)方法:图象法,定义法;
(2)定义法步骤:取值,作差变形,定号,下结论。
六、课后作业:
1、必做题:课后练习1,4,6,
2、选做题: 课后练习7
七、板书设计
函数单调性
一、函数单调性概念1、单调递增函数2、单调递减函数3、单调区间 (主板书) 二、例题及解答例1例2 (副板书) 议练活动 (辅助性板书)
4
y
y
1
-1
x
1
o
1
x
0
-1
1
-2
2
2
-4
2
1
5
4
3
1
-1
-2
-1
-5
-3
-2
3
x
o
取值
作差变形
定号
下结论
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
第二章 函数
2.1.3 函数的单调性
本节教材分析
一 三维目标
1知识与能力目标
(1) 理解函数的单调性及其几何意义。
(2) 学会运用函数图象理解和研究函数的性质.。
(3) 理解增区间、减区间等概念,掌握增(减)函数的证明和判别。
2 过程与方法目标
(1)逐步借助图像、表格、自然语言和数学符号语言,建立增(减)函数的概念。
(2)学生利用定义证明单调性,进一步加强逻辑推理能力及判断推理能力的培养
(3)培养学生利用数学语言对概念进行概括的能力。
3情感态度与价值观目标
(1) 通过本节课的教学,启发学生养成细心观察,认真分析,严谨论证的良好习惯.
(2) 通过问题链的引入,激发学生学习数学的兴趣;学生通过积极参与教学活动,获得成功的体验,锻炼克服困难的意志,建立学习的信心。
二 教学重点
函数单调性的概念和判断。
三 教学难点
利用函数单调性的定义判断具体函数的单调性。
四 教学建议
函数的单调性是函数的一个重要性质,在讲解函数单调性的概念时要结合图形进行分析说明,是抽象的概念直观化,加深概念的理解。同时也要注意培养学生应用图形解决问题的能力。
新课导入设计
导入一:分别画y=2x,y=-2x和y= +1的函数图像,引导学生观察图像的升降变化,体会不同函数在不同区间上的变化差异,从而导入新课。
导入二:列举生活中的例子 比如
(1)近六届世界杯进球数如下表: 画成折线图:
年份 进球数
1990 115
1994 137
1998 171
2002 161
2006 147
2010 145
问题1:随着年份的不同,进球数有什么变化?进球数的变化和图象的变化有什么联系?
(2)某市某天的气温变化曲线图:
问题2:随着时间的变化,温度的
变化趋势是?(上升?下降?)
通过分析这些例子导入新课。
函数的单调性
教学过程
四、教学过程:
(一)问题情境:
(1)近六届世界杯进球数如下表: 画成折线图:
年份 进球数
1990 115
1994 137
1998 171
2002 161
2006 147
2010 145
问题1:随着年份的不同,进球数有什么变化?进球数的变化和图象的变化有什么联系?
(2)绵阳市某天的气温变化曲线图:
问题2:随着时间的变化,温度的
变化趋势是?(上升?下降?)
事实上,在生活中,有很多数据的变化是有规律的,了解这些数据的变化
规律,对我们的生活很有帮助。观察满足函数关系的数据变化规律往往是看:随着自变量的变化,函数值是如何变化的,这就是我们今天要研究的函数的单调性。
(板书课题)
(二)建构定义:
1、引入直观性定义:
观察下列函数的图象,由学生讨论交流并回答下列问题(几何画板动态展示)
问题3:这两个函数图象有怎样的变化趋势?(上升?下降?)
问题4:函数在区间 内y随x的增大而增大,在区间 内
y随x的增大而减小;
总结到一般情况下:
在区间D内 在区间D内
图象
图象特征 从左到右,图象上升 从左到右,图象下降
数量特征 y随x的增大而增大 y随x的增大而减小
教师说明直观性定义:称左边的函数在区间D上单调递增函数,右边的函数则称为区间I上单调递减函数。
2、严格数学语言定义:
多媒体展示:图象在区间D内呈上升趋势
当x的值增大时,函数值y也增大
区间内有两个点、,当时,有
问题5:若区间内有两点时,有,能否推出是单调递
增函数?
构造反例,动画演示,引导学生对自变量取值的“任意性”的深刻理解。
定义:一般地,设函数的定义域为I:
如果对于定义域I内某个区间上的任意两个自变量的值,当时,都有,那么就说函数在区间上是单调递增函数。
由学生类比得到减函数的定义:
如果对于定义域I内某个区间上的任意两个自变量的值,当时,都有,那么就说函数在区间上是单调递减函数。
注:
(1)三大特征:①属于同一区间;②任意性;③有大小:通常规定;
(2)相对于定义域,函数的单调性可以是函数的局部性质。
举例:在上是单调增函数,但在整个定义域上不是增(减)函数。
(三)定义应用:
例1、下图是定义在[-5,5]上的函数的图象,根据图象说出函数的单调区间,以及在每一单调区间上,是增函数还是减函数。
分析:动画演示,帮助学生理解。
解:的单调区间有[-5,-2),[-2,1),[1,3),[3,5]。
其中在[-5,-2),[1,3)上是减函数;
在[-2,1), [3,5)上是增函数。
强调单调区间的写法:
问题6:可否写成[-5,-2)U[-2,1)?
问题7:写成[-5,-2)还是写成[-5,-2]?
多媒体展示构造反例说明:
(1)单调区间一般不能求并集;
(2)当端点满足单调性定义时,可开可闭。
例2、试判断函数 在区间(0,+∞)上是增函数还是减函数?并给予证明。
分析:问1:除了图象法判定函数单调性还有什么方法?
2:如何用定义法判定函数单调性?
3:用定义判定函数单调性的关键是什么?(提示如何比较3和2的大小,从而引入作差法)
证明:函数 在(0,+∞)上是增函数
设 是(0,+∞)上的任意两个值,且,
则
又,故,
则,即:
因此,函数 在(0,+∞)上是增函数。
总结定义法证明函数单调性的步骤:
1、取值:设任意属于给定区间,且;
2、作差变形:变形的常用方法:因式分解、配方、有理化等;
3、定号:确定的正负号;
4、下结论:由定义得出函数的单调性。
思考题:
在上面证明中,你能理解的任意性的意义吗?
解答:有了“任意性”在区间内不管取哪两个值,其证明过程都是一样的。
四、课堂练习:
(1)课本P65页1,
(2)证明:函数在上是减函数。(动画演示帮助理解)
课堂思考:
函数
单调区间
单调性
课后思考:
函数在R上单调递增,那么,的符号有什么规律?若单调递减,又该如何
五、回顾小结:
1、函数单调性的定义;
2、判定函数单调性:
(1)方法:图象法,定义法;
(2)定义法步骤:取值,作差变形,定号,下结论。
六、课后作业:
1、必做题:课后练习1,4,6,
2、选做题: 课后练习7
七、板书设计
函数单调性
一、函数单调性概念1、单调递增函数2、单调递减函数3、单调区间 (主板书) 二、例题及解答例1例2 (副板书) 议练活动 (辅助性板书)
4
y
y
1
-1
x
1
o
1
x
0
-1
1
-2
2
2
-4
2
1
5
4
3
1
-1
-2
-1
-5
-3
-2
3
x
o
取值
作差变形
定号
下结论
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
