三角形中位线定理
图片预览

文档简介
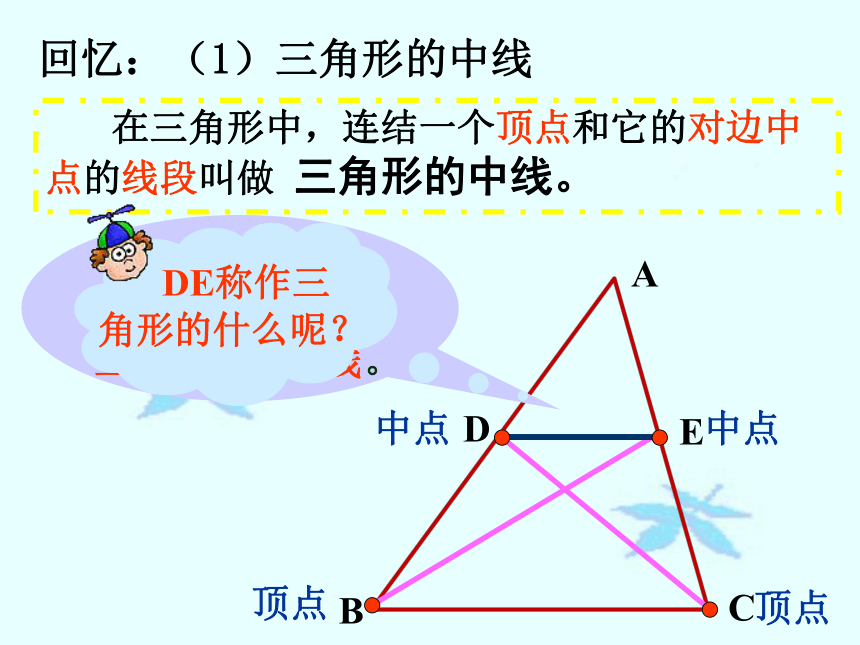
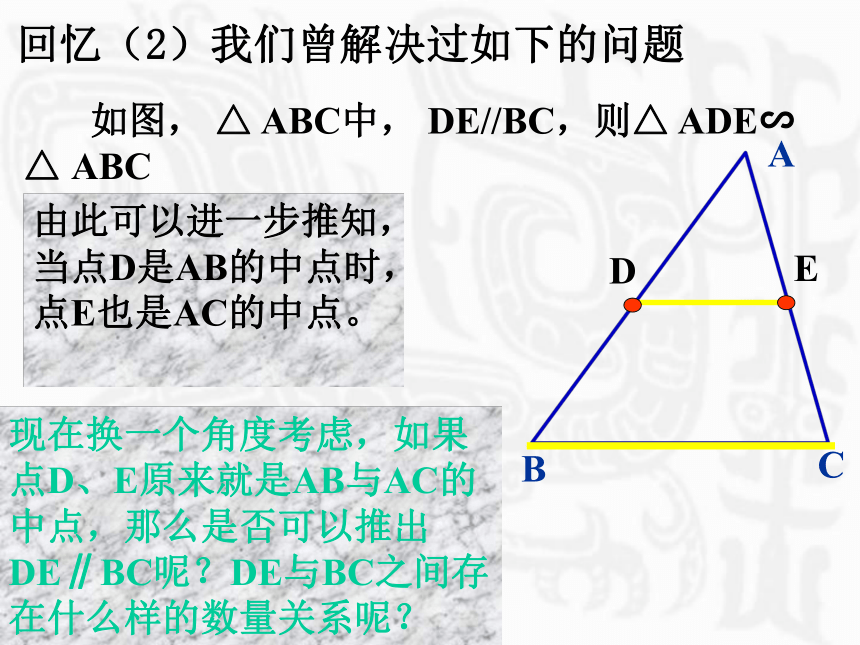
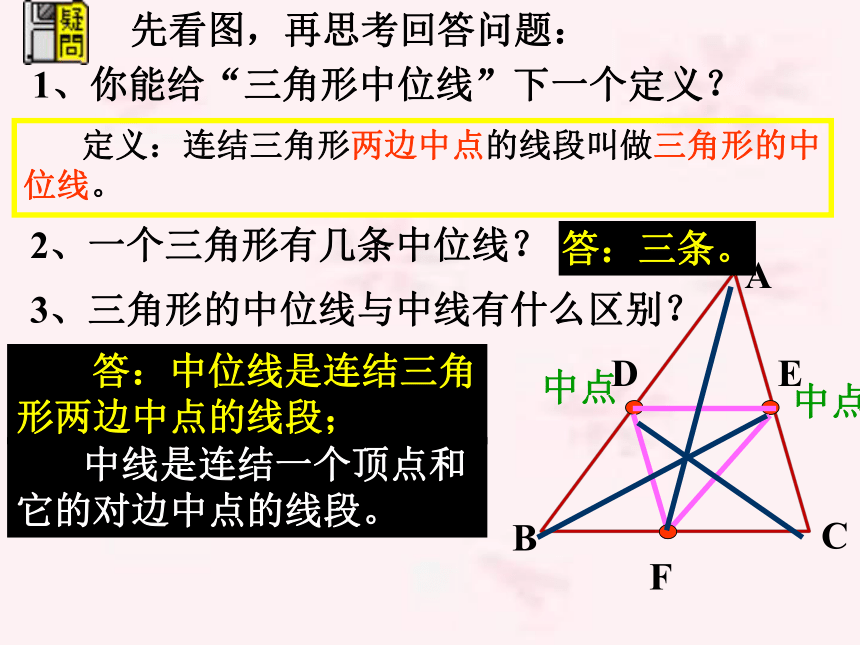
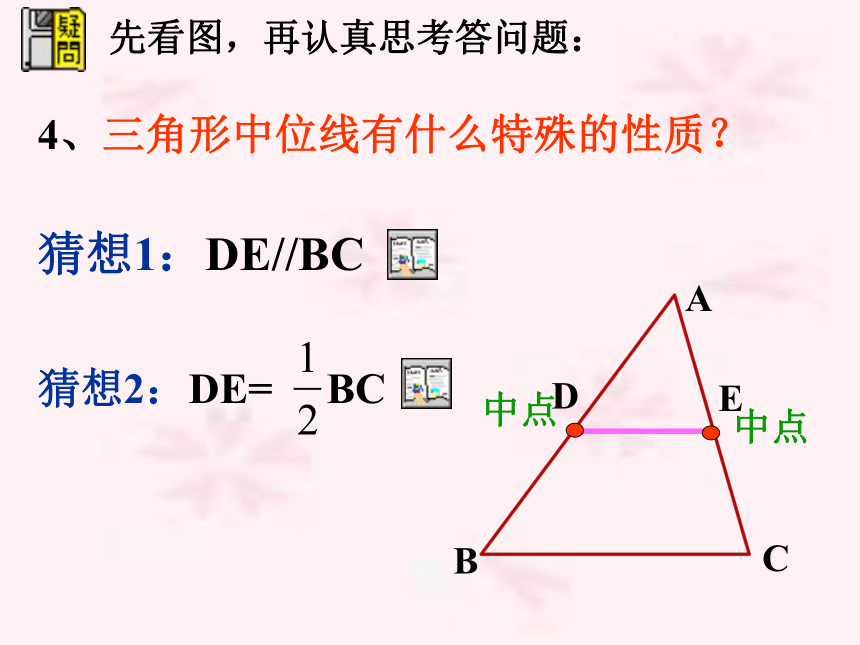
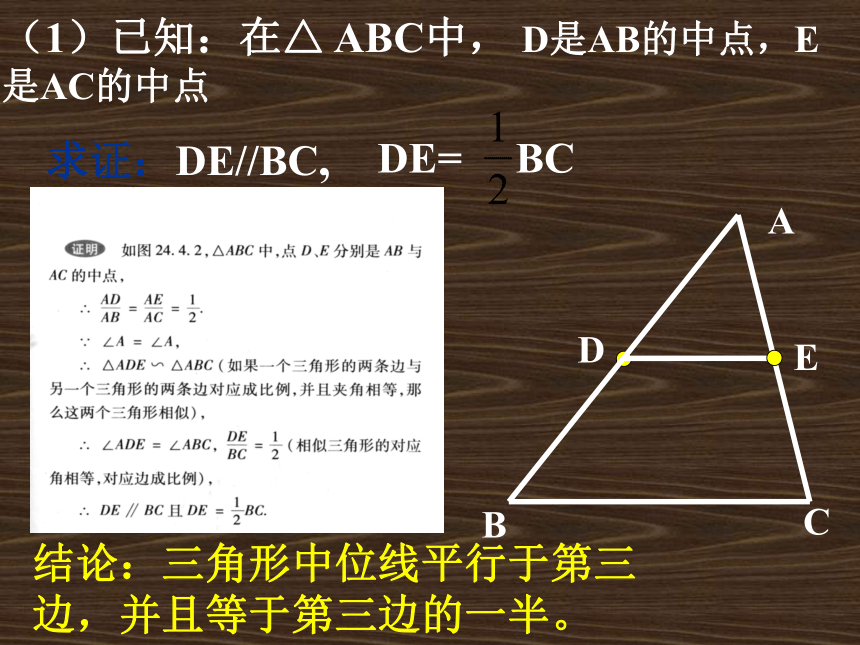
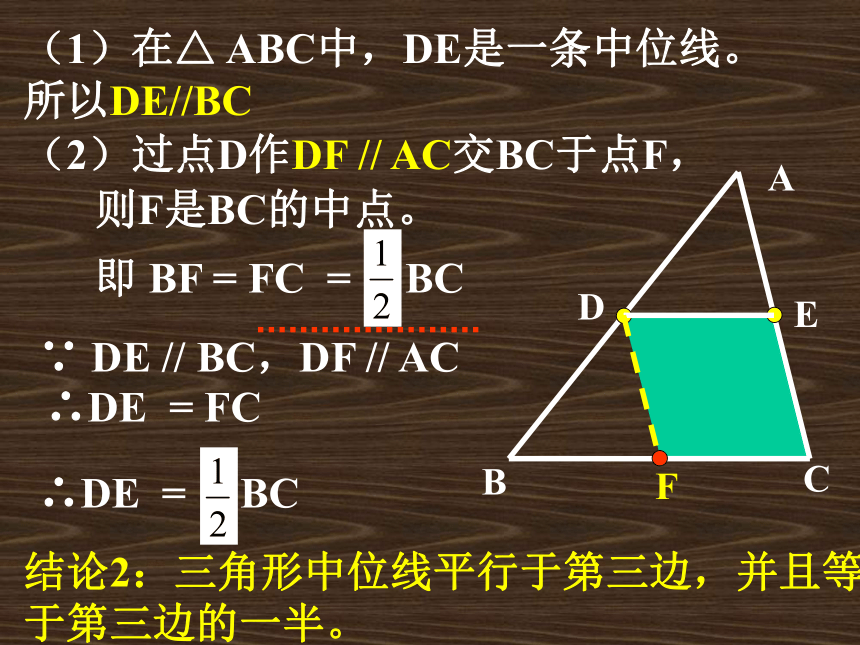
课件18张PPT。三角形中位线回忆:(1)三角形的中线 在三角形中,连结一个顶点和它的对边中点的线段叫做 三角形的中线。 它就是我们这节课要学习的三角形的中位线。由此可以进一步推知,当点D是AB的中点时,点E也是AC的中点。现在换一个角度考虑,如果点D、E原来就是AB与AC的中点,那么是否可以推出DE∥BC呢?DE与BC之间存在什么样的数量关系呢? 答:中位线是连结三角形两边中点的线段;2、一个三角形有几条中位线?3、三角形的中位线与中线有什么区别?答:三条。 中线是连结一个顶点和它的对边中点的线段。 定义:连结三角形两边中点的线段叫做三角形的中位线。先看图,再认真思考答问题:4、三角形中位线有什么特殊的性质?猜想1:DE//BC猜想2:DE= BC结论:三角形中位线平行于第三边,并且等于第三边的一半。(2)过点D作DF // AC交BC于点F,∵ DE // BC,DF // AC∴DE = FC即 BF = FC = BC∴DE = BC结论2:三角形中位线平行于第三边,并且等于第三边的一半。则F是BC的中点。三角形中位线的性质三角形中位线定理:三角形中位线平行于第三边,并且等于它的一半。三角形中位线定理有两个结论:(1)表示位置关系------平行于第三边;(2)表示数量关系------等于第三边的一半。应用时要具体分析,需要哪一个就用哪一个。己知:如图
(1)∵ E、F分别为AB、AC的中点。
∴ EF∥BC(根据? ???? )
(2)若BC =10cm,
则EF = ㎝。
(3)若EF =6cm,
则BC = cm。ABCEF三角形中位线定理512以最快的速度回答下面的问题E已知:三角形的各边分别为6cm,8cm, 10cm,则连结各边中点所成三角形的周长为 —— cm。请想一想这个问题:12【例题】求证:顺次连结四边形四条边的中点,所得的四边形是平行四边形。已知:在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。求证:四边形EFGH是平行四边形。∵AH=HD,CG=GD∴HG//AC,HG= AC(三角形中位线定理)且EF=HG所以四边形EFGH是平行四边形∴ EF//HG,例题的推广求证:顺次连结矩形四条边中点,所得的四边形是菱形。∵AH=HD,CG=GD∴HG= ACHE= GF= BD∴HG= EF=HE=GF∴四边形EFGH是菱形∵AC=BD已知:在矩形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。
求证:四边形EFGH是菱形。例题的推广求证:顺次连结矩形四条边中点,所得的四边形是菱形。EH= BD∵AC=BD∴HG= EH实际问题:
A、B两点被岛屿隔开,如何才能知道它们之间的距离呢?AB(1)在A、B外选一点C,连结A C和BC ;(2)并分别找出A C和BC的中点M、N 。(3)连结MN ,并测量MN的长度。解决方案(4)因此MN是△ ABC的中位线,根据三角形中位线定理AB=2MN。 (1) 如图,AF=FD=DB,
FG∥DE∥BC,PE=1.5。
则DP= ———,BC= ———。34.591.5PABFGECD(2)已知:△ABC三边长分别为a,b,c,它的三条中位线组成△DEF,△DEF的三条中位线又组成△HPN,则△ HPN的周长等于—————,为△ ABC周长的——, 面积为△ABC面积的—— 提高练习:1、三角形中位线是三角形中重要的线段,要与三角形的中线区分开来。小结3、证明线段倍分关系的方法常有三种:作业:课本184页第4小题,188页第8小题谢谢大家
(1)∵ E、F分别为AB、AC的中点。
∴ EF∥BC(根据? ???? )
(2)若BC =10cm,
则EF = ㎝。
(3)若EF =6cm,
则BC = cm。ABCEF三角形中位线定理512以最快的速度回答下面的问题E已知:三角形的各边分别为6cm,8cm, 10cm,则连结各边中点所成三角形的周长为 —— cm。请想一想这个问题:12【例题】求证:顺次连结四边形四条边的中点,所得的四边形是平行四边形。已知:在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。求证:四边形EFGH是平行四边形。∵AH=HD,CG=GD∴HG//AC,HG= AC(三角形中位线定理)且EF=HG所以四边形EFGH是平行四边形∴ EF//HG,例题的推广求证:顺次连结矩形四条边中点,所得的四边形是菱形。∵AH=HD,CG=GD∴HG= ACHE= GF= BD∴HG= EF=HE=GF∴四边形EFGH是菱形∵AC=BD已知:在矩形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。
求证:四边形EFGH是菱形。例题的推广求证:顺次连结矩形四条边中点,所得的四边形是菱形。EH= BD∵AC=BD∴HG= EH实际问题:
A、B两点被岛屿隔开,如何才能知道它们之间的距离呢?AB(1)在A、B外选一点C,连结A C和BC ;(2)并分别找出A C和BC的中点M、N 。(3)连结MN ,并测量MN的长度。解决方案(4)因此MN是△ ABC的中位线,根据三角形中位线定理AB=2MN。 (1) 如图,AF=FD=DB,
FG∥DE∥BC,PE=1.5。
则DP= ———,BC= ———。34.591.5PABFGECD(2)已知:△ABC三边长分别为a,b,c,它的三条中位线组成△DEF,△DEF的三条中位线又组成△HPN,则△ HPN的周长等于—————,为△ ABC周长的——, 面积为△ABC面积的—— 提高练习:1、三角形中位线是三角形中重要的线段,要与三角形的中线区分开来。小结3、证明线段倍分关系的方法常有三种:作业:课本184页第4小题,188页第8小题谢谢大家
