图形数列
图片预览
文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
第二类 已知图形数列,求通项公式
曲靖市第二中学 陈世忠
以几何图形为依托的数列,题意新颗、构思精巧,极富思考性、挑战性和趣味性,是典型的具有时代气息的信息迁移题。此类题型能充分体现变知识立意为能力,具有较好的区分度和选拔功能, 备受各级各类考试命题者的青睐,频频出现在各级各类考试卷中,不但要求学生对数列知识掌握较好,而且还要提高自己的观察能力,发现从中的规律性。现就近几年高考模拟试题中出现的与图形有关的数列通项的考题进行分类解析,旨在探索题型规律.揭示解题方法.
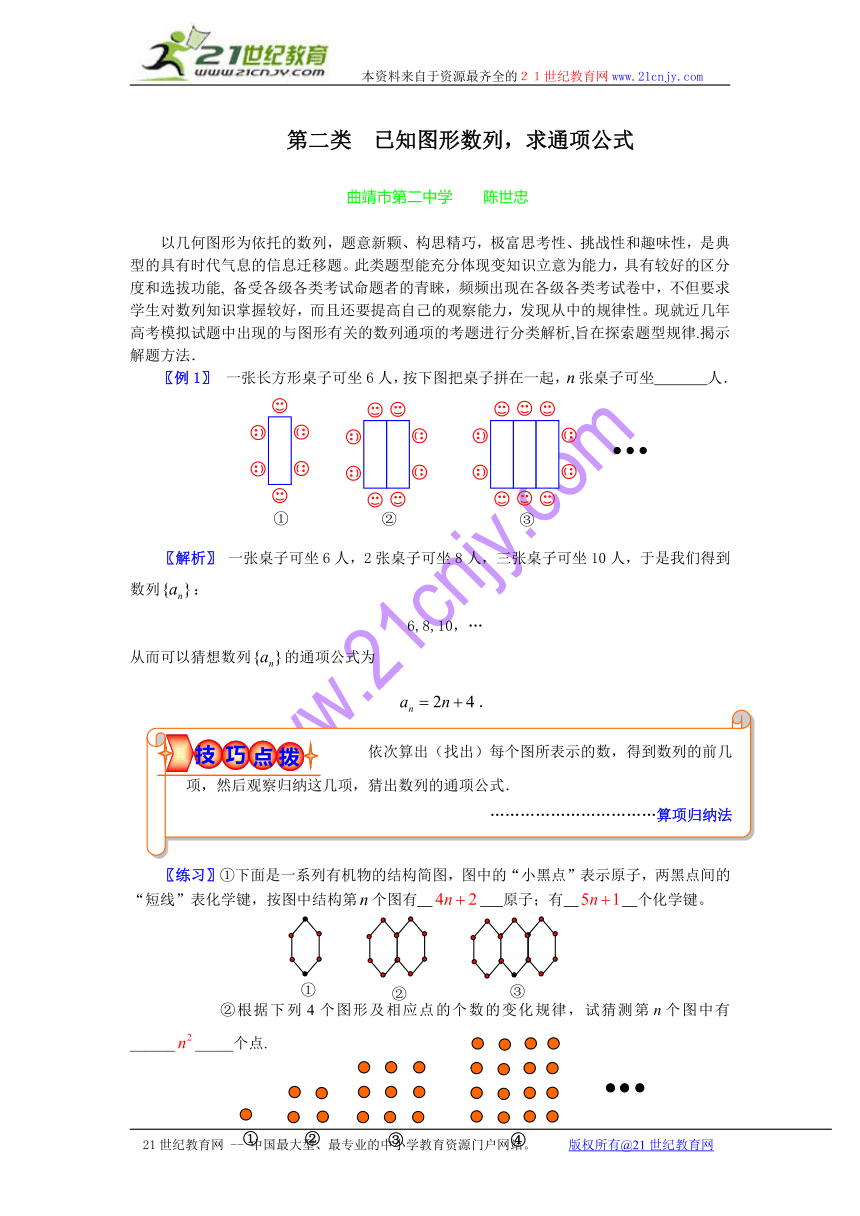
〖例1〗 一张长方形桌子可坐6人,按下图把桌子拼在一起,张桌子可坐 人.
〖解析〗 一张桌子可坐6人,2张桌子可坐8人,三张桌子可坐10人,于是我们得到数列:
6,8,10,…
从而可以猜想数列的通项公式为
.
〖练习〗①下面是一系列有机物的结构简图,图中的“小黑点”表示原子,两黑点间的“短线”表化学键,按图中结构第个图有 原子;有 个化学键。
②根据下列4个图形及相应点的个数的变化规律,试猜测第个图中有___________个点.
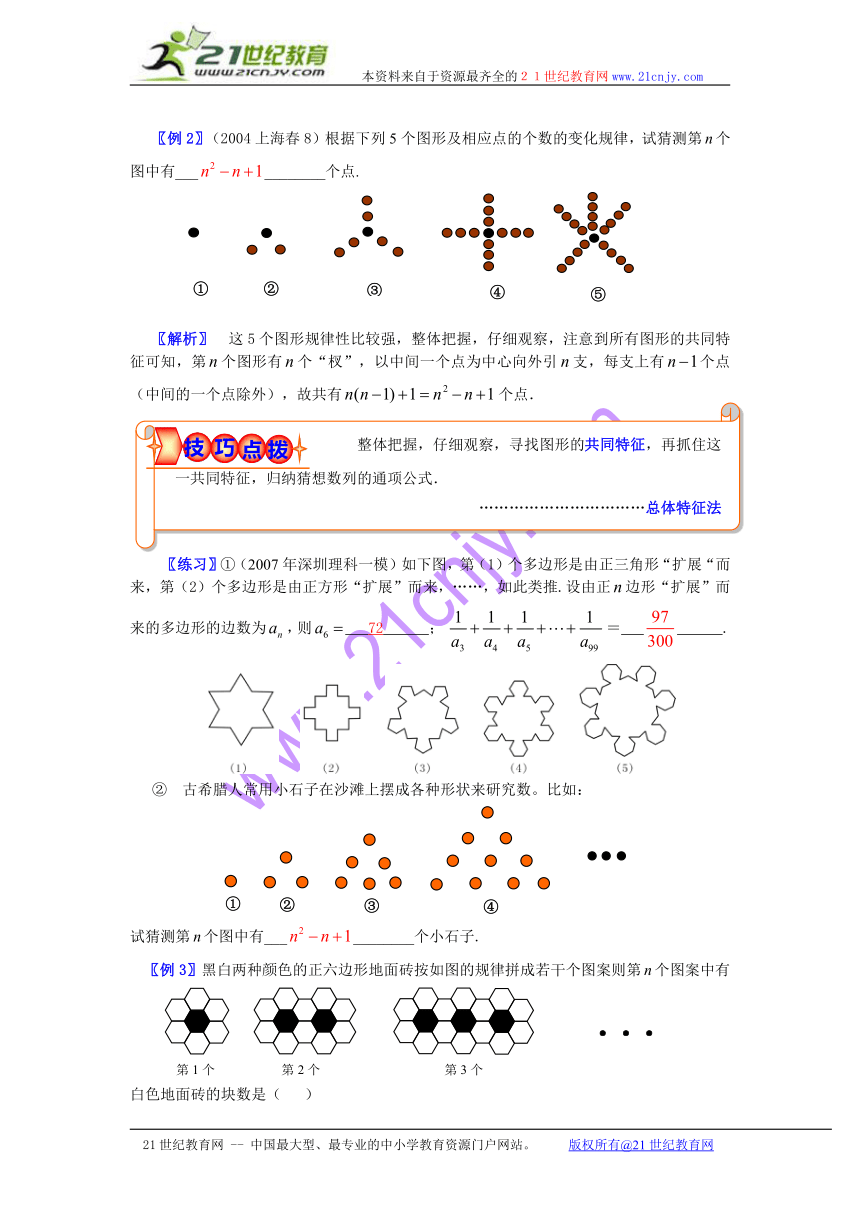
〖例2〗(2004上海春8)根据下列5个图形及相应点的个数的变化规律,试猜测第个图中有___________个点.
〖解析〗 这5个图形规律性比较强,整体把握,仔细观察,注意到所有图形的共同特征可知,第个图形有个“杈”,以中间一个点为中心向外引支,每支上有个点(中间的一个点除外),故共有个点.
〖练习〗①(2007年深圳理科一模)如下图,第(1)个多边形是由正三角形“扩展“而来,第(2)个多边形是由正方形“扩展”而来,……,如此类推.设由正边形“扩展”而来的多边形的边数为,则 72 ; = .
② 古希腊人常用小石子在沙滩上摆成各种形状来研究数。比如:
试猜测第个图中有___________个小石子.
〖例3〗黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案则第个图案中有白色地面砖的块数是( )
A. B. C. D.
〖解析〗 注意到前后图形很接近,仔细观察发现后一个图是由前一个图形变化而来,找到变化规律,问题就解决了,把这个图形按如下规律分解:
发现从第二个图形开始后一个图形比前一个图形多4块白色地面砖,这就是说:
设第个图案中白色地面砖的块数为,则
且,
从而数列是以6为首项,4为公差的等差数,由等差数列的通项公式得
.
〖练习〗① 图中的三角形称为谢宾斯基(Sierpinski)三角形。在下图4个三角形中,着色三角形的个数依次构成一个数列的前4项,则这个数列的一个通项公式为 .
②下面是一系列有机物的结构简图,图中的“小黑点”表示原子,两黑点间的“短线”表化学键,按图中结构第个图有 原子;有 个化学键。
解:(1)每个结构简图去掉最左边两个原子后,每个环上有4个原子,第个结构简图有个环,所以原子数共有个.
(2)每个结构简图去掉最左边的一个化学键后,每个环上有5个化学键,故第个结构简图有个化学键.
点评:本题抓住每个“环”上的原子数、化学键,找出其一般规律。
③(2006广东—理14)在德国不来梅举行的第48届世乒赛期间,某商店橱窗里用同样的乒乓球堆成若干堆“正三棱锥”形的展品,其中第1堆只有1层,就一个球;第堆最底层(第一层)分别按图2所示方式固定摆放,从第二层开始,每层的小球自然垒放在下一层之上,第堆第层就放一个乒乓球,以表示第堆的乒乓球总数,则 10 ;(答案用表示).
②
①
③
技
巧
点
拨
依次算出(找出)每个图所表示的数,得到数列的前几项,然后观察归纳这几项,猜出数列的通项公式.
……………………………算项归纳法
①
②
③
①
②
③
④
①
②
③
④
⑤
技
巧
点
拨
整体把握,仔细观察,寻找图形的共同特征,再抓住这一共同特征,归纳猜想数列的通项公式.
……………………………总体特征法
③
①
②
④
第1个
第2个
第3个
···
第2个
第3个
第1个
第2个
技
巧
点
拨
注意到前后图形很接近,后一个图形是在前一个图形的基础上变化得到的,找到这种变化规律,即找到递推关系,问题就解决了.
……………………………递推公式法
①
②
③
(2006广东—14)
第一层
第二层
第一层
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
第二类 已知图形数列,求通项公式
曲靖市第二中学 陈世忠
以几何图形为依托的数列,题意新颗、构思精巧,极富思考性、挑战性和趣味性,是典型的具有时代气息的信息迁移题。此类题型能充分体现变知识立意为能力,具有较好的区分度和选拔功能, 备受各级各类考试命题者的青睐,频频出现在各级各类考试卷中,不但要求学生对数列知识掌握较好,而且还要提高自己的观察能力,发现从中的规律性。现就近几年高考模拟试题中出现的与图形有关的数列通项的考题进行分类解析,旨在探索题型规律.揭示解题方法.
〖例1〗 一张长方形桌子可坐6人,按下图把桌子拼在一起,张桌子可坐 人.
〖解析〗 一张桌子可坐6人,2张桌子可坐8人,三张桌子可坐10人,于是我们得到数列:
6,8,10,…
从而可以猜想数列的通项公式为
.
〖练习〗①下面是一系列有机物的结构简图,图中的“小黑点”表示原子,两黑点间的“短线”表化学键,按图中结构第个图有 原子;有 个化学键。
②根据下列4个图形及相应点的个数的变化规律,试猜测第个图中有___________个点.
〖例2〗(2004上海春8)根据下列5个图形及相应点的个数的变化规律,试猜测第个图中有___________个点.
〖解析〗 这5个图形规律性比较强,整体把握,仔细观察,注意到所有图形的共同特征可知,第个图形有个“杈”,以中间一个点为中心向外引支,每支上有个点(中间的一个点除外),故共有个点.
〖练习〗①(2007年深圳理科一模)如下图,第(1)个多边形是由正三角形“扩展“而来,第(2)个多边形是由正方形“扩展”而来,……,如此类推.设由正边形“扩展”而来的多边形的边数为,则 72 ; = .
② 古希腊人常用小石子在沙滩上摆成各种形状来研究数。比如:
试猜测第个图中有___________个小石子.
〖例3〗黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案则第个图案中有白色地面砖的块数是( )
A. B. C. D.
〖解析〗 注意到前后图形很接近,仔细观察发现后一个图是由前一个图形变化而来,找到变化规律,问题就解决了,把这个图形按如下规律分解:
发现从第二个图形开始后一个图形比前一个图形多4块白色地面砖,这就是说:
设第个图案中白色地面砖的块数为,则
且,
从而数列是以6为首项,4为公差的等差数,由等差数列的通项公式得
.
〖练习〗① 图中的三角形称为谢宾斯基(Sierpinski)三角形。在下图4个三角形中,着色三角形的个数依次构成一个数列的前4项,则这个数列的一个通项公式为 .
②下面是一系列有机物的结构简图,图中的“小黑点”表示原子,两黑点间的“短线”表化学键,按图中结构第个图有 原子;有 个化学键。
解:(1)每个结构简图去掉最左边两个原子后,每个环上有4个原子,第个结构简图有个环,所以原子数共有个.
(2)每个结构简图去掉最左边的一个化学键后,每个环上有5个化学键,故第个结构简图有个化学键.
点评:本题抓住每个“环”上的原子数、化学键,找出其一般规律。
③(2006广东—理14)在德国不来梅举行的第48届世乒赛期间,某商店橱窗里用同样的乒乓球堆成若干堆“正三棱锥”形的展品,其中第1堆只有1层,就一个球;第堆最底层(第一层)分别按图2所示方式固定摆放,从第二层开始,每层的小球自然垒放在下一层之上,第堆第层就放一个乒乓球,以表示第堆的乒乓球总数,则 10 ;(答案用表示).
②
①
③
技
巧
点
拨
依次算出(找出)每个图所表示的数,得到数列的前几项,然后观察归纳这几项,猜出数列的通项公式.
……………………………算项归纳法
①
②
③
①
②
③
④
①
②
③
④
⑤
技
巧
点
拨
整体把握,仔细观察,寻找图形的共同特征,再抓住这一共同特征,归纳猜想数列的通项公式.
……………………………总体特征法
③
①
②
④
第1个
第2个
第3个
···
第2个
第3个
第1个
第2个
技
巧
点
拨
注意到前后图形很接近,后一个图形是在前一个图形的基础上变化得到的,找到这种变化规律,即找到递推关系,问题就解决了.
……………………………递推公式法
①
②
③
(2006广东—14)
第一层
第二层
第一层
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
