数学:《相互独立事件同时发生的概率》 课件(新人教B版选修)
文档属性
| 名称 | 数学:《相互独立事件同时发生的概率》 课件(新人教B版选修) |

|
|
| 格式 | rar | ||
| 文件大小 | 280.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-03-05 00:00:00 | ||
图片预览








文档简介
课件23张PPT。相互独立事件同时
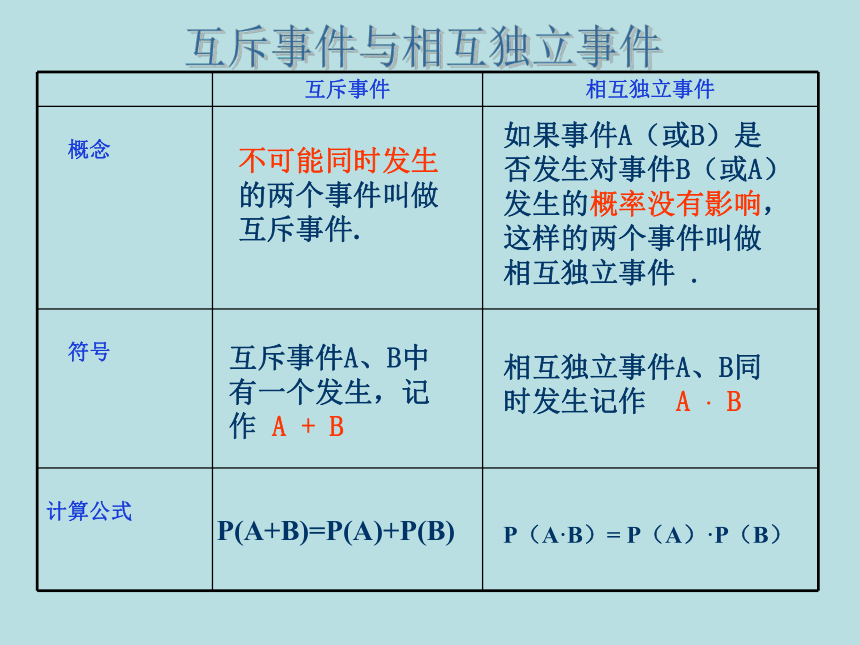
发生的概率(2)1.相互独立事件及其同时发生的概率不可能同时发生的两个事件叫做互斥事件.如果事件A(或B)是否发生对事件B(或A)发生的概率没有影响,这样的两个事件叫做相互独立事件 .P(A+B)=P(A)+P(B)P(A·B)= P(A)·P(B) 互斥事件A、B中有一个发生,记作 A + B相互独立事件A、B同时发生记作 A · B互斥事件与相互独立事件中国女排以11战全胜的战绩夺得2003年日本世界杯冠军.20年后重登奥运之巅 中国女排雅典圆梦2004年雅典奥运会女子排球决赛在中国和俄罗斯之间展开,最终中国女排在先失两局的不利情况下连扳三局,以总比分3-2击败俄罗斯女排获得冠军,这也是中国女排继1984年洛杉矶奥运会夺冠以来第二次在奥运会女排比赛中摘金,这是女排姑娘的骄傲!也是全中国人民的骄傲!!!
假如经过多年的努力,男排实力明显提高,到2008年北京奥运会时,凭借着天时、地利、人和的优势,男排夺冠的概率有0.7;女排继续保持现有水平,夺冠的概率有0.9。那么,男、女排双双夺冠的概率有多大?变式1:只有女排夺冠的概率有多大?典型例题变式训练变式2:恰有一队夺冠的概率有多大?变式3:至少有一队夺冠的概率有多大?变式4:至少有一队不夺冠的概率有多大?例1. 假如到2008年北京奥运会时,凭借着天时、地利、人和的优势,男排夺冠的概率有0.7;女排夺冠的概率有0.9.那么,男女排双双夺冠的概率有多大?解:设事件A:女排夺冠,事件B:男排夺冠,
则男女排双双夺冠的概率为: 答:男女排双双夺冠的概率为0.63.变式一 只有女排夺冠的概率有多大?略解: 只有女排夺冠的概率为例1. 假如到2008年北京奥运会时,凭借着天时、地利、人和的优势,男排夺冠的概率有0.7;女排夺冠的概率有0.9.那么,男女排双双夺冠的概率有多大?解:设事件A:女排夺冠,事件B:男排夺冠, 变式二:只有一队夺冠的概率有多大?略解:只有一队夺冠的概率有多大为:例1. 假如到2008年北京奥运会时,凭借着天时、地利、人和的优势,男排夺冠的概率有0.7;女排夺冠的概率有0.9.那么,男女排双双夺冠的概率有多大?变式三: 至少有一队夺冠的概率有多大?解1:(正向思考)至少有一队夺冠的概率为例1. 假如到2008年北京奥运会时,凭借着天时、地利、人和的优势,男排夺冠的概率有0.7;女排夺冠的概率有0.9.那么,男女排双双夺冠的概率有多大?变式三: 至少有一队夺冠的概率有多大?解2:(逆向思考)至少有一队夺冠的概率为 例2.有三批种子,其发芽率分别为0.9、0.8和0.7,在每批种子中各随机抽取一粒,求至少有一粒种子发芽的概率 解:设第一批种子发芽为事件A,同样第二、三批种子发芽分别为事件B、C,设至少有一粒种子发芽为事件D,则同理可算出等号右边的其他各项 对于n个随机事件A1、A2、…、An,事件A1+A2+…+An由两个对立事件的概率和等于1,可得表示事件A1、A2、…、An至少有一个发生,即A1、A2、…、An都不发生概率的和与积的互补公式 例2.有三批种子,其发芽率分别为0.9、0.8和0.7,在每批种子中各随机抽取一粒,求至少有一粒种子发芽的概率 解:设第一批种子发芽为事件A,同样第二、三批种子发芽分别为事件B、C,设至少有一粒种子发芽为事件D,则和例3.甲、乙两个人独立地破译一个密码,他们能译出密码的概率分别为 ,求
(1)两个人都译出密码的概率;(2)两个人都译不出密码的概率;
(3)恰有1个人译出密码的概率;(4)至多1个人译出密码的概率;
(5)至少1个人译出密码的概率解:(1)两个人都译出密码的概率为:(2)两个人都译不出密码的概率为:(3)恰有1个人译出密码可以分为两类:甲译出乙未译出以及甲未译出乙译出,且两个事件为互斥事件,所以恰有1个人译出密码的概率为:(4)“至多1个人译出密码”的对立事件为“有两个人译出密码”,所以至多1个人译出密码的概率为:(5)“至少有1个人译出密码”的对立事件为“两人未译出密码”,所以至少有1个人译出密码的概率为:例4.如图,开关电路中,某段时间内,开关a、b、c开或关的概率均为0.5,且是相互独立的,求这段时间内灯亮的概率.解:分别记“开关a合上”、“开关b合上”、“开关c合上”为事件A、B、C,由已知,A、B、C是相互独立事件且概率都是0.5.
开关a、b合上或开关c合上时灯亮,所以这段时间内灯亮的概率为:例5.掷三颗骰子,试求:
(1)没有一颗骰子出现1点或6点的概率;
(2)恰好有一颗骰子出现1点或6点的概率.
(3)至少有1颗骰子出现1点或6点的概率是多少 解:记“第1颗骰子出现1点或6点”为事件A,
“第2颗骰子出现1点或6点”为事件B,
“第3颗骰子出现1点或6点”为事件C,
由已知A、B、C是相互独立事件,(1)没有1颗骰子出现1点或6点,也就是事件A、B、C全不发生,
即事件所以所求概率为:例5.掷三颗骰子,试求:
(1)没有一颗骰子出现1点或6点的概率;
(2)恰好有一颗骰子出现1点或6点的概率.
(3)至少有1颗骰子出现1点或6点的概率是多少 (2)恰好有1颗骰子出现1点或6点,即A发生B不发生C不发生或A不发生B发生C不发生或A不发生B不发生C发生,用符号表示为事件例5.掷三颗骰子,试求:
(1)没有一颗骰子出现1点或6点的概率;
(2)恰好有一颗骰子出现1点或6点的概率.
(3)至少有1颗骰子出现1点或6点的概率是多少 (3)“至少有1颗骰子出现1点或6点”的对立事件为“没有一颗骰子出现1点或6点,即问题(1)中的事件,所求概率为例6.某工厂的产品要同时经过两名检验员检验合格方能出厂,但在检验时也可能出现差错,将合格产品不能通过检验或将不合格产品通过检验,对于两名检验员,合格品不能通过检验的概率分别为?1、?2,不合格产品通过检验的概率分别为?1、?2,两名检验员的工作独立.
求:(1)一件合格品不能出厂的概率,
(2)一件不合格产品能出厂的概率 解:(1)记“一件合格品通过第 I 名检验员检验”为事件Ai(i=1、2)
“一件合格品不能通过检验出厂”的对立事件为“一件合格品同时通过两名检验员检验”,即事件A1·A2发生
所以所求概率为
1?P(A1·A2)=1?P(A1)·P(A2)=1?(1??1)(1??2)=?1+?2??1?2例6.某工厂的产品要同时经过两名检验员检验合格方能出厂,但在检验时也可能出现差错,将合格产品不能通过检验或将不合格产品通过检验,对于两名检验员,合格品不能通过检验的概率分别为?1、?2,不合格产品通过检验的概率分别为?1、?2,两名检验员的工作独立.
求:(1)一件合格品不能出厂的概率,
(2)一件不合格产品能出厂的概率 (2)“一件不合格品能通过第i名检验员检验”记为事件Bi(i=1、2),
“一件不合格品能出厂”即不合格品通过两名检验员检验
事件B1· B2发生,所求概率为:
P(B1· B2)=P(B1)·P(B2)=?1· ?2两台机床加工同样的零件,第一台出废品的概率是0.03,第二台出废品的概率是0.02.加工出来的零件堆放在一起.若第一台加工的零件是第二台加工的零件的2倍,求任意取出的零件是合格品的概率 记“任意取出的零件是合格品”为事件A,则“任意取出的零件是废品”为两个事件相互独立,是指它们其中一个事件的发生与否对另一个事件发生的概率没有影响.
一般地,两个事件不可能既互斥又相互独立,因为互斥事件是不可能同时发生的,而相互独立事件是以它们能够同时发生为前提的.
相互独立事件同时发生的概率等于每个事件发生的概率的积,这一点与互斥事件的概率和也是不同的.
发生的概率(2)1.相互独立事件及其同时发生的概率不可能同时发生的两个事件叫做互斥事件.如果事件A(或B)是否发生对事件B(或A)发生的概率没有影响,这样的两个事件叫做相互独立事件 .P(A+B)=P(A)+P(B)P(A·B)= P(A)·P(B) 互斥事件A、B中有一个发生,记作 A + B相互独立事件A、B同时发生记作 A · B互斥事件与相互独立事件中国女排以11战全胜的战绩夺得2003年日本世界杯冠军.20年后重登奥运之巅 中国女排雅典圆梦2004年雅典奥运会女子排球决赛在中国和俄罗斯之间展开,最终中国女排在先失两局的不利情况下连扳三局,以总比分3-2击败俄罗斯女排获得冠军,这也是中国女排继1984年洛杉矶奥运会夺冠以来第二次在奥运会女排比赛中摘金,这是女排姑娘的骄傲!也是全中国人民的骄傲!!!
假如经过多年的努力,男排实力明显提高,到2008年北京奥运会时,凭借着天时、地利、人和的优势,男排夺冠的概率有0.7;女排继续保持现有水平,夺冠的概率有0.9。那么,男、女排双双夺冠的概率有多大?变式1:只有女排夺冠的概率有多大?典型例题变式训练变式2:恰有一队夺冠的概率有多大?变式3:至少有一队夺冠的概率有多大?变式4:至少有一队不夺冠的概率有多大?例1. 假如到2008年北京奥运会时,凭借着天时、地利、人和的优势,男排夺冠的概率有0.7;女排夺冠的概率有0.9.那么,男女排双双夺冠的概率有多大?解:设事件A:女排夺冠,事件B:男排夺冠,
则男女排双双夺冠的概率为: 答:男女排双双夺冠的概率为0.63.变式一 只有女排夺冠的概率有多大?略解: 只有女排夺冠的概率为例1. 假如到2008年北京奥运会时,凭借着天时、地利、人和的优势,男排夺冠的概率有0.7;女排夺冠的概率有0.9.那么,男女排双双夺冠的概率有多大?解:设事件A:女排夺冠,事件B:男排夺冠, 变式二:只有一队夺冠的概率有多大?略解:只有一队夺冠的概率有多大为:例1. 假如到2008年北京奥运会时,凭借着天时、地利、人和的优势,男排夺冠的概率有0.7;女排夺冠的概率有0.9.那么,男女排双双夺冠的概率有多大?变式三: 至少有一队夺冠的概率有多大?解1:(正向思考)至少有一队夺冠的概率为例1. 假如到2008年北京奥运会时,凭借着天时、地利、人和的优势,男排夺冠的概率有0.7;女排夺冠的概率有0.9.那么,男女排双双夺冠的概率有多大?变式三: 至少有一队夺冠的概率有多大?解2:(逆向思考)至少有一队夺冠的概率为 例2.有三批种子,其发芽率分别为0.9、0.8和0.7,在每批种子中各随机抽取一粒,求至少有一粒种子发芽的概率 解:设第一批种子发芽为事件A,同样第二、三批种子发芽分别为事件B、C,设至少有一粒种子发芽为事件D,则同理可算出等号右边的其他各项 对于n个随机事件A1、A2、…、An,事件A1+A2+…+An由两个对立事件的概率和等于1,可得表示事件A1、A2、…、An至少有一个发生,即A1、A2、…、An都不发生概率的和与积的互补公式 例2.有三批种子,其发芽率分别为0.9、0.8和0.7,在每批种子中各随机抽取一粒,求至少有一粒种子发芽的概率 解:设第一批种子发芽为事件A,同样第二、三批种子发芽分别为事件B、C,设至少有一粒种子发芽为事件D,则和例3.甲、乙两个人独立地破译一个密码,他们能译出密码的概率分别为 ,求
(1)两个人都译出密码的概率;(2)两个人都译不出密码的概率;
(3)恰有1个人译出密码的概率;(4)至多1个人译出密码的概率;
(5)至少1个人译出密码的概率解:(1)两个人都译出密码的概率为:(2)两个人都译不出密码的概率为:(3)恰有1个人译出密码可以分为两类:甲译出乙未译出以及甲未译出乙译出,且两个事件为互斥事件,所以恰有1个人译出密码的概率为:(4)“至多1个人译出密码”的对立事件为“有两个人译出密码”,所以至多1个人译出密码的概率为:(5)“至少有1个人译出密码”的对立事件为“两人未译出密码”,所以至少有1个人译出密码的概率为:例4.如图,开关电路中,某段时间内,开关a、b、c开或关的概率均为0.5,且是相互独立的,求这段时间内灯亮的概率.解:分别记“开关a合上”、“开关b合上”、“开关c合上”为事件A、B、C,由已知,A、B、C是相互独立事件且概率都是0.5.
开关a、b合上或开关c合上时灯亮,所以这段时间内灯亮的概率为:例5.掷三颗骰子,试求:
(1)没有一颗骰子出现1点或6点的概率;
(2)恰好有一颗骰子出现1点或6点的概率.
(3)至少有1颗骰子出现1点或6点的概率是多少 解:记“第1颗骰子出现1点或6点”为事件A,
“第2颗骰子出现1点或6点”为事件B,
“第3颗骰子出现1点或6点”为事件C,
由已知A、B、C是相互独立事件,(1)没有1颗骰子出现1点或6点,也就是事件A、B、C全不发生,
即事件所以所求概率为:例5.掷三颗骰子,试求:
(1)没有一颗骰子出现1点或6点的概率;
(2)恰好有一颗骰子出现1点或6点的概率.
(3)至少有1颗骰子出现1点或6点的概率是多少 (2)恰好有1颗骰子出现1点或6点,即A发生B不发生C不发生或A不发生B发生C不发生或A不发生B不发生C发生,用符号表示为事件例5.掷三颗骰子,试求:
(1)没有一颗骰子出现1点或6点的概率;
(2)恰好有一颗骰子出现1点或6点的概率.
(3)至少有1颗骰子出现1点或6点的概率是多少 (3)“至少有1颗骰子出现1点或6点”的对立事件为“没有一颗骰子出现1点或6点,即问题(1)中的事件,所求概率为例6.某工厂的产品要同时经过两名检验员检验合格方能出厂,但在检验时也可能出现差错,将合格产品不能通过检验或将不合格产品通过检验,对于两名检验员,合格品不能通过检验的概率分别为?1、?2,不合格产品通过检验的概率分别为?1、?2,两名检验员的工作独立.
求:(1)一件合格品不能出厂的概率,
(2)一件不合格产品能出厂的概率 解:(1)记“一件合格品通过第 I 名检验员检验”为事件Ai(i=1、2)
“一件合格品不能通过检验出厂”的对立事件为“一件合格品同时通过两名检验员检验”,即事件A1·A2发生
所以所求概率为
1?P(A1·A2)=1?P(A1)·P(A2)=1?(1??1)(1??2)=?1+?2??1?2例6.某工厂的产品要同时经过两名检验员检验合格方能出厂,但在检验时也可能出现差错,将合格产品不能通过检验或将不合格产品通过检验,对于两名检验员,合格品不能通过检验的概率分别为?1、?2,不合格产品通过检验的概率分别为?1、?2,两名检验员的工作独立.
求:(1)一件合格品不能出厂的概率,
(2)一件不合格产品能出厂的概率 (2)“一件不合格品能通过第i名检验员检验”记为事件Bi(i=1、2),
“一件不合格品能出厂”即不合格品通过两名检验员检验
事件B1· B2发生,所求概率为:
P(B1· B2)=P(B1)·P(B2)=?1· ?2两台机床加工同样的零件,第一台出废品的概率是0.03,第二台出废品的概率是0.02.加工出来的零件堆放在一起.若第一台加工的零件是第二台加工的零件的2倍,求任意取出的零件是合格品的概率 记“任意取出的零件是合格品”为事件A,则“任意取出的零件是废品”为两个事件相互独立,是指它们其中一个事件的发生与否对另一个事件发生的概率没有影响.
一般地,两个事件不可能既互斥又相互独立,因为互斥事件是不可能同时发生的,而相互独立事件是以它们能够同时发生为前提的.
相互独立事件同时发生的概率等于每个事件发生的概率的积,这一点与互斥事件的概率和也是不同的.
