1.2.1函数概念

课件23张PPT。1.2.1函数的概念学习目标: 1、理解函数的概念，区分运动学、集合学的观点定义函数的异同点;
2、了解构成函数的三要素;
3、会判断给出的两个函数是否是 同一函数;
4、会用区间和数轴来表示集合。（1）正、反比例函数
（2）一次函数
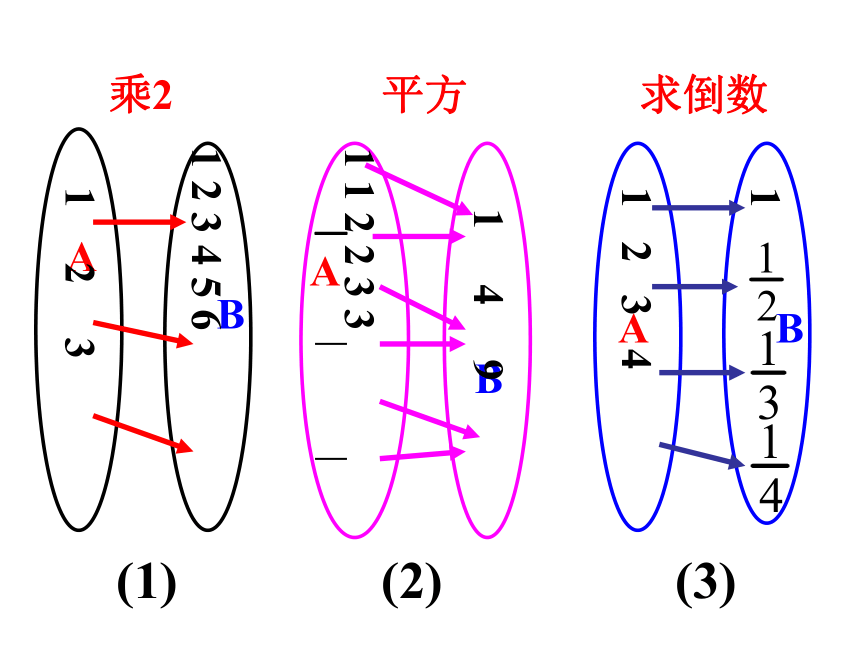
（3）二次函数 初中学过的函数:函数?思考: (1) y=1(x∈R)是函数吗？AAABBB 1 2 3 1 2 3 4 5 6 1 1 2 2 3 3 1 4 9 －－－ 1 2 3 4 1 (1)(2)(3)乘2平方求倒数函数实际上就是从自变量Ｘ的集合到函数值Ｙ的集合的一种对应关系。 若把初中函数概念中的自变量x的取值范围和函数值y的取值范围分别看成集合A和B，就是我们今天要学习的概念。一、函数的概念: 设A，B是非空的数集，如果按照某种确定的对应关系f，使对于集合A中的任意一个数x，在集合B中都有唯一确定的数f(x)和它对应，那么就称f：A→B为从集合A到集合B的一个函数，记作 y=f(x)，x∈A.
其中，x叫做自变量，自变量的取值范围A叫做函数的定义域；与x值相对应的y值叫做函数值，函数值的集合{f(x)|x∈A}叫做函数的值域。注意：(2)定义域,值域,对应法则f 称为函数的三要素。集合B不一定是函数的值域,函数的值域是集合B的子集。实际上值域由定义域和对应法则f 确定。(3)两个函数相同必须是它们的定义域、值域和对应法则完全相同，但表示自变量和函数值的符号可以不同。 (1)集合A，B连同对应法则f一起，称集合A到集合B的一个函数，千万别误解为仅对应法则f为函数。(4)有时给出的函数没有明确说明定义域,这时它的定义域就是自变量的允许取值范围。(5)常用f(a)表示函数y=f(x)当x=a时的函数值。函数还可用h(x)、g(x)、F(x)、G(x)等来表示。注意：例题讲解： 一次函数y=ax+b(a≠0)定义域是R.值域是R. 二次函数y=ax2+bx+c (a≠0) 的定义域是R.值域是当a＞0时,为:当a＜0时,为:☆ 下列图像中不能作为函数的是( )（Ａ）（Ｂ）（Ｃ）（Ｄ）B注意唯一性解（1） 有意义的实数x的集合是{x|x≥-3}

有意义的实数x的集合是{x|x≠2}
所以这个函数的定义域就是
（2）（3）因为a>0,所以f（a），f（a-1）有意义前面的问题：判断两个函数是否是同一函数的方法： 1、 两个函数的定义域和对应法则完全相同，即称这两个函数相等（或为同一函数）。
2、 两个函数相等当且仅当它们的定义域和对应法则完全相同，而与表示自变量和函数值的字母无关。3练习2:下列四组中的函数表示同一函数的是（ ）(A)(B)(C)(D)D设a、b是两个实数，且a 1、对于[a,b]，(a,b)，[a,b)，(a,b]都称数a和数b为区间的端点，其中a为左端点，b为右端点，称b-a为区间长度；
2、书写区间记号时：有完整的区间外围记号（上述四者之一）；
3、有两个区间端点，且左端点小于右端点；
4、两个端点之间用“，”隔开;5、在数轴上，这些区间都可以用一条以a和b为端点的线段来表示，在图中，用实心点表示包括在区间内的端点，用空心点表示不包括在区间内的端点; 6、实数集R也可以用区间表示为(-∞，+∞)，
“∞”读作“无穷大”，“-∞”读作“负无穷大”，
“+∞”读作“正无穷大”，还可以把满足x≥a,
x>a, x≤b, x[a,+∞)、(a,+∞)、(-∞,b]、(-∞,b)。 集合表示区间表示数轴表示{x a＜x＜b}(a , b)。。{x a≤x≤b}[a , b]..{x a≤x＜b}[a , b).。{x a＜x≤b}(a , b].。{x x＜a}(－∞, a)。{x x≤a}(－∞, a].{x x＞b}(b , +∞)。{x x≥b}[b , +∞).{x x∈R}(－∞,+∞)数轴上所有的点核心概念知识?方法?思想函数【总一总★成竹在胸】下课