第七章 平面图形的认识 ------复习课
文档属性
| 名称 | 第七章 平面图形的认识 ------复习课 |

|
|
| 格式 | rar | ||
| 文件大小 | 37.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-03-06 00:00:00 | ||
图片预览






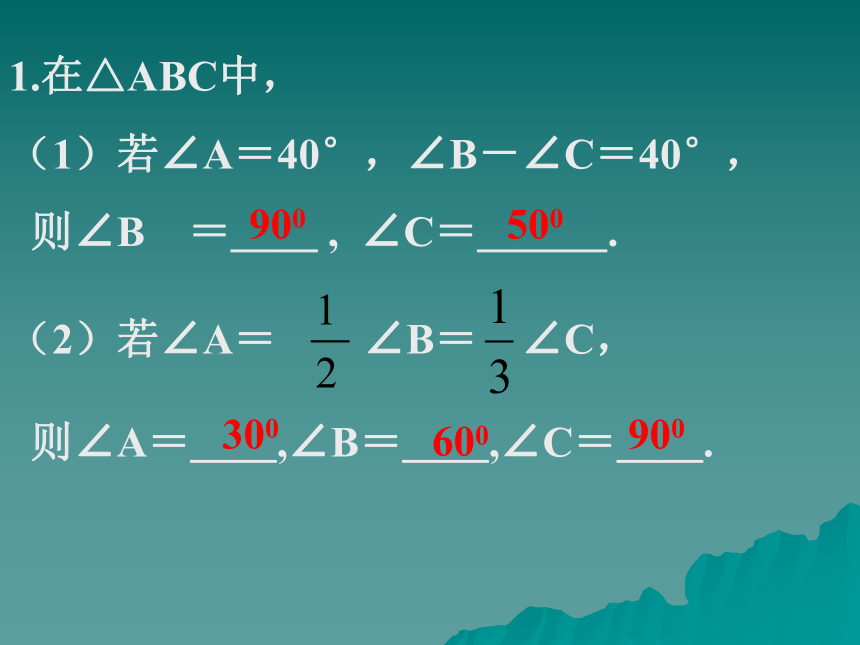
文档简介
课件17张PPT。第七章 平面图形的认识
复习课知识点回顾:1.你知道如何判定两条直线是否平行吗?方法1: 同位角相等,两直线平行
方法2: 内错角相等,两直线平行
方法3: 同旁内角互补,两直线平行
方法4: 平行线的定义
方法5: 平行公理的推论
方法6: 在同一平面内,垂直于同一条直 线的所有直线平行(需要说明过程)2.你知道两直线平行有什么性质吗?性质1:两直线平行,同位角相等
性质2:两直线平行,内错角相等
性质3:两直线平行,同旁内角互补
性质4:两平行线之间的距离相等
性质5:如果两个角的两边分别平行,
那么这两个角相等或互补。3.图形的平移 ⑴图形的平移的要素:方向、距离。
⑵图形平移的性质:
①图形的平移不改变图形的形状与大小, 只改变位置.
②图形平移后,对应点的连线平行(或在同一直线上)且相等.
4.认识三角形⑴三角形的分类:
⑵三角形的三条重要线段:
角平分线、中线、高
①三角形有3条高,3条角平分线,3条中线 ②三角形3条高,3条角平分线,3条中线所在直线分别相交于一点。5.三角形的三边之间的关系
6.三角形的三角之间的关系
7.多边形的内角和
8.多边形的外角和三角形的任意一边大于其它两边的差,小于其它两边的和。三角形的三个内角和为1800n边形的内角和为(n-2)1800n边形的外角和为36001.在△ABC中,
(1)若∠A=40°,∠B-∠C=40°,
则∠B =__ , ∠C=___.
(2)若∠A= ∠B= ∠C,
则∠A=__,∠B=__,∠C=__.900500300600900
2.如图,在△ABC中,∠A、∠B的平
分线相交于点I,若∠C=700,则∠AIB
=__,若∠AIB=1550,则∠C= .
3.如图,
∠1+∠2+∠3+∠4+∠5+∠6=__ 1250130036004.锐角三角形ABC中,3条高相交于点H,
若∠BAC=70°,则∠BHC=___。
5.已知:三角形的3边长分别为1,x,5,
且x为整数,则x=_____。
6.如图,∠O的两边被一直线所截,用α和β的式子表示∠O的度数为( )
A.α-β B.β-α
C.180°-α+β D.180°-α-β
11005B7.如图把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,∠A与∠1+∠2之间的数量关系保持不变,请找一找这个规律,你发现的规律是 ( )
A.∠A=∠1+∠2 B.2∠A=∠1+∠2
C.3∠A=2∠1+∠2 D.3∠A=2(∠1+∠2)B8.若一个多边形的内角和是外角和的3.5倍,则此多边形的边数是( )
A. 7 B. 14 C. 9 D. 18
10.直角三角形两锐角的平分线所交成的角的度数是( )
A. 45° B. 135°
C. 45°或135° D. 以上答案都不对C C11.如图,在△ABC中,∠BAC=4∠ABC=4∠C,BD⊥AC,垂足为D,求∠ABD的度数。 12.在△ABC中,∠B>∠C,AD为∠BAC的平分线,AE⊥BC,垂足为E,
试说明∠DAE= (∠B-∠C)13.已知如图∠xOy=900,BE是∠ABy的平分线,BE的反向延长线与∠OAB的平分线相交于点C,当点A,B分别在射线Ox,Oy上移动时,试问∠ACB的大小是否发生变化?如果保持不变,请说明理由;如果随点A,B的移动而变化,请求出变化范围。解:在△ABC中根据外角的性质,
∠ACB=∠EBA-∠BAC而BE平分∠yBA,AC平分∠BAO
∴∠EBA= ∠yBA,∠BAC= ∠BAO∴∠ACB= (∠yBA-∠BAO)在△ABO中,根据外角的性质,得
∠yBA-∠BAO=∠AOB=900∴∠ACB=450即∠ACB的大小保持不变,且等于45度。14.如图,AB∥DC,ED∥BC,AE∥BD,写出图中与△ABD面积相等的三角形。解:由DC∥AB得
S△ABD=S△ABC 由AE∥BD得
S△ABD=S△EBD 由ED∥BC得
S△EBD=S△EDC15.如图,P为△ABC内任意一点,试比较AB+AC与PB+PC的大小,并说明理由。D解:延长BP交AC于D在△ABD中,根据三角形三边关系得AB+AD>BP+PD①在△PDC中,同理可得
PD+DC>PC②①+②得:
AB+AD+PD+DC>BP+PD+PC则,AB+AC>BP+PC
方法2: 内错角相等,两直线平行
方法3: 同旁内角互补,两直线平行
方法4: 平行线的定义
方法5: 平行公理的推论
方法6: 在同一平面内,垂直于同一条直 线的所有直线平行(需要说明过程)2.你知道两直线平行有什么性质吗?性质1:两直线平行,同位角相等
性质2:两直线平行,内错角相等
性质3:两直线平行,同旁内角互补
性质4:两平行线之间的距离相等
性质5:如果两个角的两边分别平行,
那么这两个角相等或互补。3.图形的平移 ⑴图形的平移的要素:方向、距离。
⑵图形平移的性质:
①图形的平移不改变图形的形状与大小, 只改变位置.
②图形平移后,对应点的连线平行(或在同一直线上)且相等.
4.认识三角形⑴三角形的分类:
⑵三角形的三条重要线段:
角平分线、中线、高
①三角形有3条高,3条角平分线,3条中线 ②三角形3条高,3条角平分线,3条中线所在直线分别相交于一点。5.三角形的三边之间的关系
6.三角形的三角之间的关系
7.多边形的内角和
8.多边形的外角和三角形的任意一边大于其它两边的差,小于其它两边的和。三角形的三个内角和为1800n边形的内角和为(n-2)1800n边形的外角和为36001.在△ABC中,
(1)若∠A=40°,∠B-∠C=40°,
则∠B =__ , ∠C=___.
(2)若∠A= ∠B= ∠C,
则∠A=__,∠B=__,∠C=__.900500300600900
2.如图,在△ABC中,∠A、∠B的平
分线相交于点I,若∠C=700,则∠AIB
=__,若∠AIB=1550,则∠C= .
3.如图,
∠1+∠2+∠3+∠4+∠5+∠6=__ 1250130036004.锐角三角形ABC中,3条高相交于点H,
若∠BAC=70°,则∠BHC=___。
5.已知:三角形的3边长分别为1,x,5,
且x为整数,则x=_____。
6.如图,∠O的两边被一直线所截,用α和β的式子表示∠O的度数为( )
A.α-β B.β-α
C.180°-α+β D.180°-α-β
11005B7.如图把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,∠A与∠1+∠2之间的数量关系保持不变,请找一找这个规律,你发现的规律是 ( )
A.∠A=∠1+∠2 B.2∠A=∠1+∠2
C.3∠A=2∠1+∠2 D.3∠A=2(∠1+∠2)B8.若一个多边形的内角和是外角和的3.5倍,则此多边形的边数是( )
A. 7 B. 14 C. 9 D. 18
10.直角三角形两锐角的平分线所交成的角的度数是( )
A. 45° B. 135°
C. 45°或135° D. 以上答案都不对C C11.如图,在△ABC中,∠BAC=4∠ABC=4∠C,BD⊥AC,垂足为D,求∠ABD的度数。 12.在△ABC中,∠B>∠C,AD为∠BAC的平分线,AE⊥BC,垂足为E,
试说明∠DAE= (∠B-∠C)13.已知如图∠xOy=900,BE是∠ABy的平分线,BE的反向延长线与∠OAB的平分线相交于点C,当点A,B分别在射线Ox,Oy上移动时,试问∠ACB的大小是否发生变化?如果保持不变,请说明理由;如果随点A,B的移动而变化,请求出变化范围。解:在△ABC中根据外角的性质,
∠ACB=∠EBA-∠BAC而BE平分∠yBA,AC平分∠BAO
∴∠EBA= ∠yBA,∠BAC= ∠BAO∴∠ACB= (∠yBA-∠BAO)在△ABO中,根据外角的性质,得
∠yBA-∠BAO=∠AOB=900∴∠ACB=450即∠ACB的大小保持不变,且等于45度。14.如图,AB∥DC,ED∥BC,AE∥BD,写出图中与△ABD面积相等的三角形。解:由DC∥AB得
S△ABD=S△ABC 由AE∥BD得
S△ABD=S△EBD 由ED∥BC得
S△EBD=S△EDC15.如图,P为△ABC内任意一点,试比较AB+AC与PB+PC的大小,并说明理由。D解:延长BP交AC于D在△ABD中,根据三角形三边关系得AB+AD>BP+PD①在△PDC中,同理可得
PD+DC>PC②①+②得:
AB+AD+PD+DC>BP+PD+PC则,AB+AC>BP+PC
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
