锐角三角函数1
图片预览


文档简介
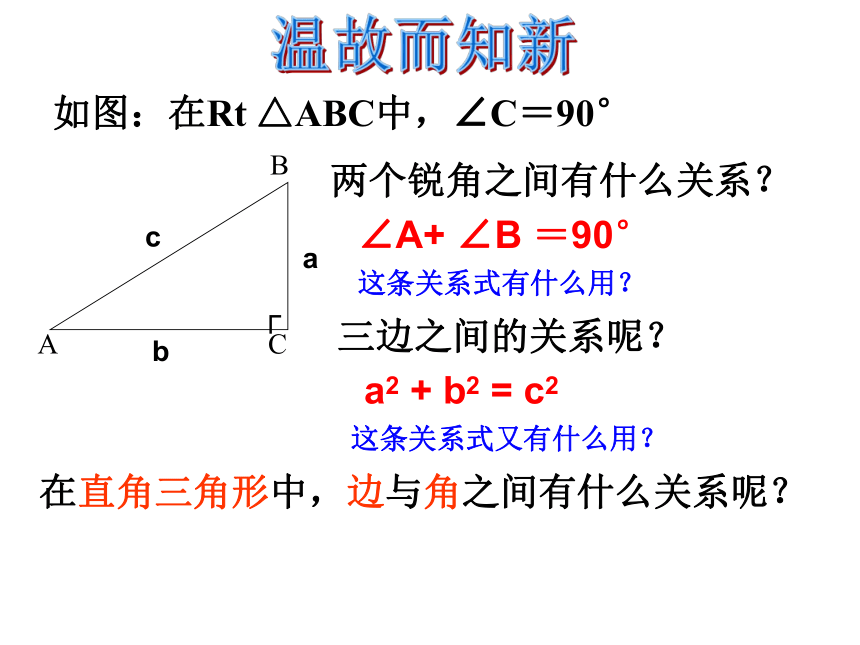
课件15张PPT。28.1锐角三角函数如图:在Rt △ABC中,∠C=90°两个锐角之间有什么关系?三边之间的关系呢?在直角三角形中,边与角之间有什么关系呢?温故而知新∠A+ ∠B =90°a2 + b2 = c2这条关系式有什么用?这条关系式又有什么用? 去年冬我国遭受了50年一遇的雪灾。某村扬水站的管道也被冻坏。为了尽快恢复生产需更换。现测得斜坡与水平面所成角的度数是30°为了使出水口的高度BC为30米,那么需要准备水管(AB)的长是多少?ABC生活中的数学当∠A=30°时当BC=40m时,AB的
长又是多少呢?
你发现在Rt△ABC中,当∠A=30°时, ∠A的对边与对边的比值是多少?
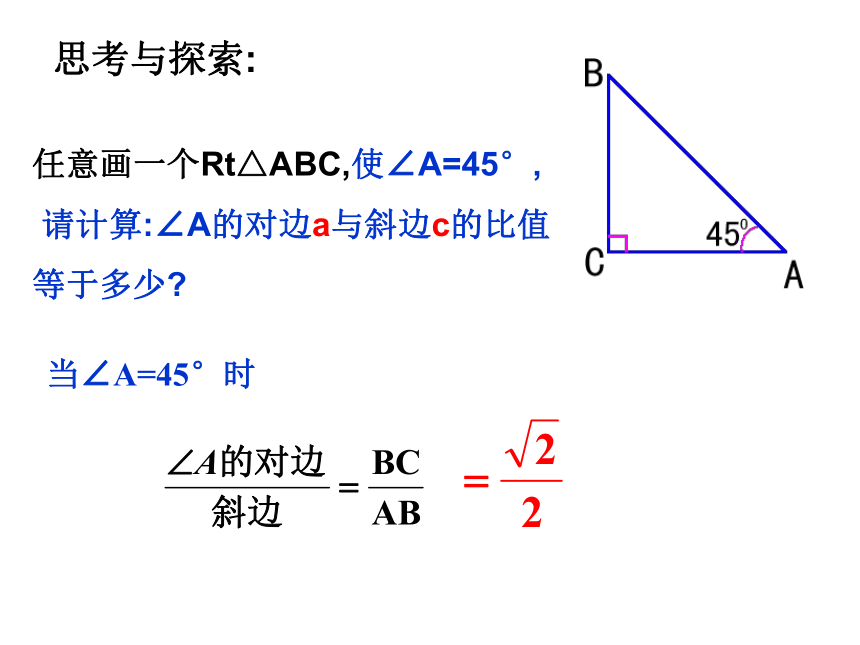
6080米当∠A=45°时任意画一个Rt△ABC,使∠A=45°,
请计算:∠A的对边a与斜边c的比值
等于多少?
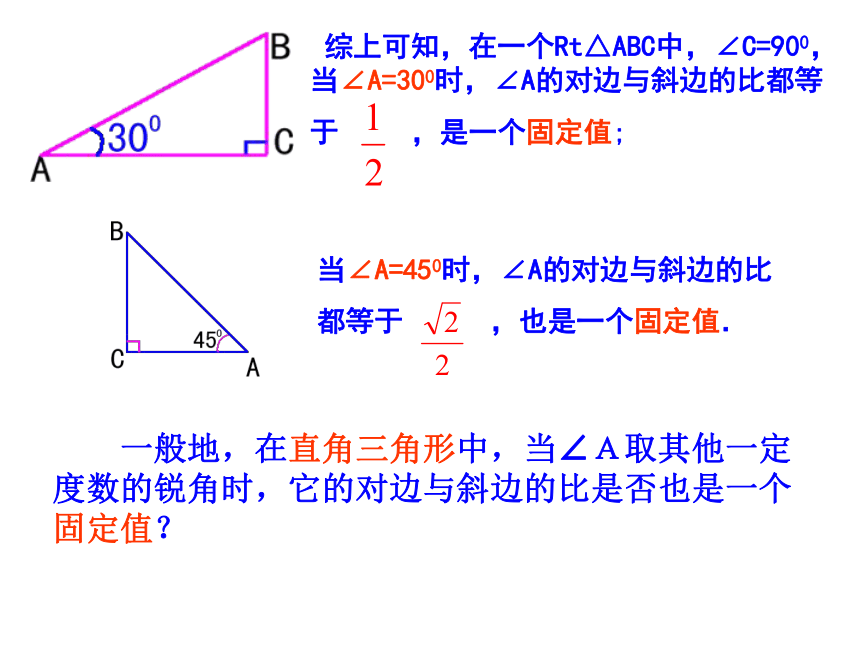
思考与探索:当∠A=450时,∠A的对边与斜边的比
都等于 ,也是一个固定值. 一般地,在直角三角形中,当∠A取其他一定度数的锐角时,它的对边与斜边的比是否也是一个固定值? 综上可知,在一个Rt△ABC中,∠C=900, 当∠A=300时,∠A的对边与斜边的比都等
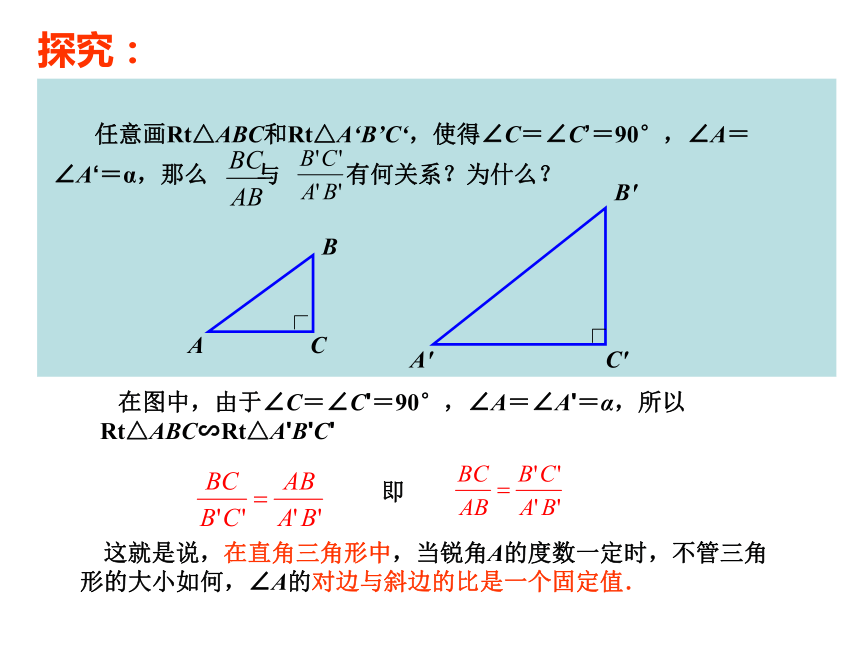
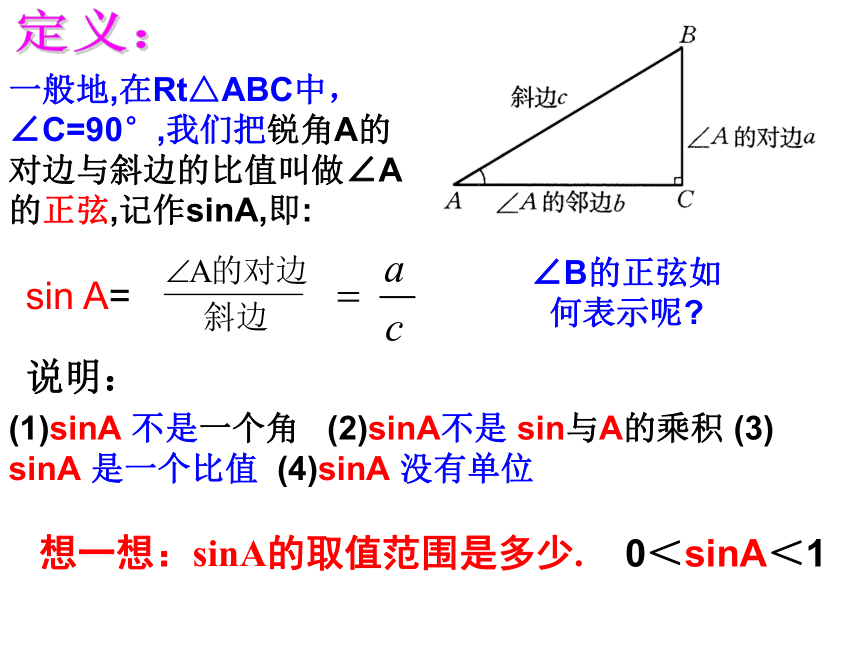
于 ,是一个固定值; 在图中,由于∠C=∠C'=90°,∠A=∠A'=α,所以Rt△ABC∽Rt△A'B'C' 这就是说,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比是一个固定值. 任意画Rt△ABC和Rt△A‘B’C‘,使得∠C=∠C’=90°,∠A=∠A‘=α,那么 与 有何关系?为什么?探究:即一般地,在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比值叫做∠A的正弦,记作sinA,即:sin A= ∠B的正弦如何表示呢?定义:想一想:sinA的取值范围是多少.(1)sinA 不是一个角 (2)sinA不是 sin与A的乘积 (3) sinA 是一个比值 (4)sinA 没有单位
说明:0<sinA<1练一练1.判断对错:√√××sinA是一个比值(注意比的顺序),无单位;×3.在Rt△ABC中,锐角A的对边和斜边同时扩大
100倍,sinA的值( )
A.扩大100倍 B.缩小
C.不变 D.不能确定C练一练( )×4、如图,P为角a的一边OA上的任一点,过P作PQ ⊥OB于点Q,则a的正弦函数值与( )
A、角a的大小无关 B、点P的位位置无关
C、角a的度数无关 D、OP的长度有关OPABQa5.如图,在Rt △ABC中,∠C=90°,AB=13,BC=5
求sinA和sinB的值.解:在Rt △ABC中, 求sinA就是要确定∠A的对边与斜边的比,求sinB就是要确定∠B的对边与斜边的比.练一练练一练6、已知点P(3,4)是∠ 边OA上的一点求sin 的值?A
求一个角的正弦值,除了用定义直接求外,还可以转化为求和它相等角的正弦值。 7、如图, ∠C=90°CD⊥AB.
sinB可以由哪两条线段之比?想一想若AC=5,CD=3,求sinB的值.解: ∵∠B=∠ACD ∴sinB=sin∠ACD在Rt△ACD中,AD=sin ∠ACD=∴sinB==4 要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α一般要满足0.77≤ sinα ≤0.97.现有一个长6m的梯子,问使用这个梯子能安全攀上一个5m 高的平房吗?用一用回味无穷1.锐角三角函数定义:2.sinA是∠A的函数. 3.只有不断的思考,才会有新的发现;只有量的变化,才会有质的进步.Sin300 =sin45°=
长又是多少呢?
你发现在Rt△ABC中,当∠A=30°时, ∠A的对边与对边的比值是多少?
6080米当∠A=45°时任意画一个Rt△ABC,使∠A=45°,
请计算:∠A的对边a与斜边c的比值
等于多少?
思考与探索:当∠A=450时,∠A的对边与斜边的比
都等于 ,也是一个固定值. 一般地,在直角三角形中,当∠A取其他一定度数的锐角时,它的对边与斜边的比是否也是一个固定值? 综上可知,在一个Rt△ABC中,∠C=900, 当∠A=300时,∠A的对边与斜边的比都等
于 ,是一个固定值; 在图中,由于∠C=∠C'=90°,∠A=∠A'=α,所以Rt△ABC∽Rt△A'B'C' 这就是说,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比是一个固定值. 任意画Rt△ABC和Rt△A‘B’C‘,使得∠C=∠C’=90°,∠A=∠A‘=α,那么 与 有何关系?为什么?探究:即一般地,在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比值叫做∠A的正弦,记作sinA,即:sin A= ∠B的正弦如何表示呢?定义:想一想:sinA的取值范围是多少.(1)sinA 不是一个角 (2)sinA不是 sin与A的乘积 (3) sinA 是一个比值 (4)sinA 没有单位
说明:0<sinA<1练一练1.判断对错:√√××sinA是一个比值(注意比的顺序),无单位;×3.在Rt△ABC中,锐角A的对边和斜边同时扩大
100倍,sinA的值( )
A.扩大100倍 B.缩小
C.不变 D.不能确定C练一练( )×4、如图,P为角a的一边OA上的任一点,过P作PQ ⊥OB于点Q,则a的正弦函数值与( )
A、角a的大小无关 B、点P的位位置无关
C、角a的度数无关 D、OP的长度有关OPABQa5.如图,在Rt △ABC中,∠C=90°,AB=13,BC=5
求sinA和sinB的值.解:在Rt △ABC中, 求sinA就是要确定∠A的对边与斜边的比,求sinB就是要确定∠B的对边与斜边的比.练一练练一练6、已知点P(3,4)是∠ 边OA上的一点求sin 的值?A
求一个角的正弦值,除了用定义直接求外,还可以转化为求和它相等角的正弦值。 7、如图, ∠C=90°CD⊥AB.
sinB可以由哪两条线段之比?想一想若AC=5,CD=3,求sinB的值.解: ∵∠B=∠ACD ∴sinB=sin∠ACD在Rt△ACD中,AD=sin ∠ACD=∴sinB==4 要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α一般要满足0.77≤ sinα ≤0.97.现有一个长6m的梯子,问使用这个梯子能安全攀上一个5m 高的平房吗?用一用回味无穷1.锐角三角函数定义:2.sinA是∠A的函数. 3.只有不断的思考,才会有新的发现;只有量的变化,才会有质的进步.Sin300 =sin45°=
