一次函数的图象及性质
图片预览




文档简介
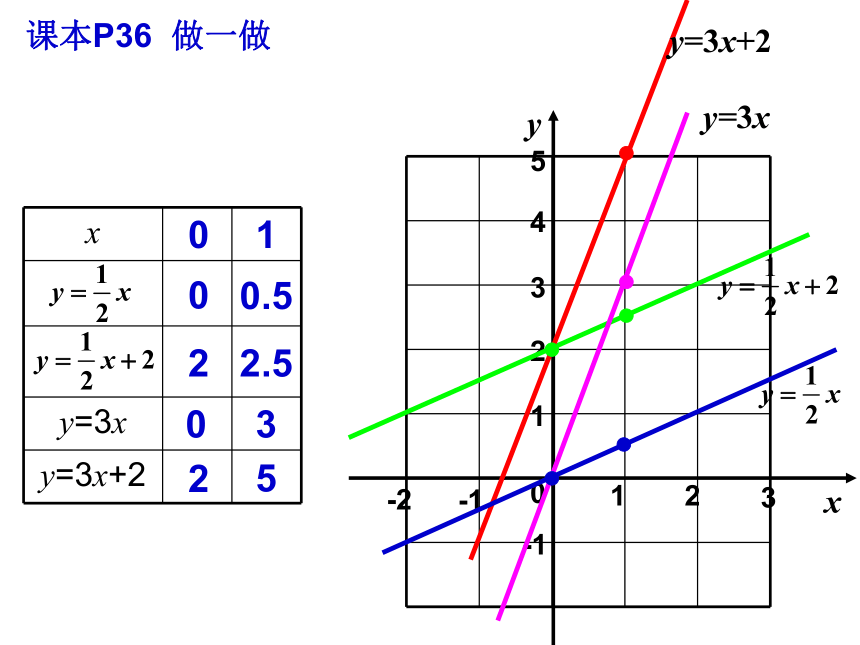
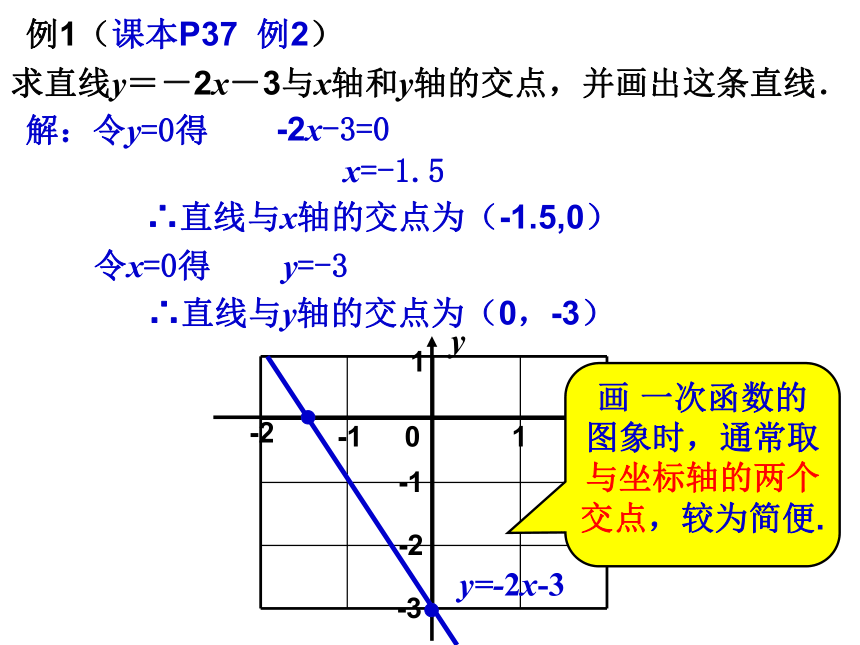
课件18张PPT。§18.3.2 一次函数的图象和性质1、一次函数的概念:解析式用自变量的一次整式表示的函数称为一次函数 .2、一次函数的解析式:y=kx+b(k、b是常数,且k≠0)当b=0时,y=kx( k≠0 )正比例函数1、已知函数 ,当m= 时,它是正比例函数.2、已知一次函数 ,则k= .2-1课本P36 做一做0100.522.50325543210-1123-1-2yy=3xy=3x+2x求直线y=-2x-3与x轴和y轴的交点,并画出这条直线.例1(课本P37 例2)解:令y=0得 -2x-3=0 x=-1.5∴直线与x轴的交点为(-1.5,0)令x=0得 y=-3∴直线与y轴的交点为(0,-3)012-1-21-1-2-3xy画 一次函数的图象时,通常取与坐标轴的两个交点,较为简便.y=-2x-3例1 在同一平面直角坐标系中画下列函数的图象.
(1) y=2x与y=2x-3;
(2) y=2x+1与y= . 课本P37 例1010002-31.5-11212-1-2-3y=2xy=2x-3
(0,1)(-0.5,0)(0,1)(-2,0)12-1-212-1y=2x+1
1.求下列直线与x轴和y轴的交点,并在同一直角坐标系中画出它们的图象:课本P38 练习1(1) y=4x-1; (2)y=解:⑴令y=0得 4x-1=0 x=0.25∴直线与x轴的交点为(0.25,0)令x=0得 y=-1∴直线与y轴的交点为(0,-1)课本P41 习题5分别在同一直角坐标系内画出下列直线,并指出每一小题中两条直线的位置关系.
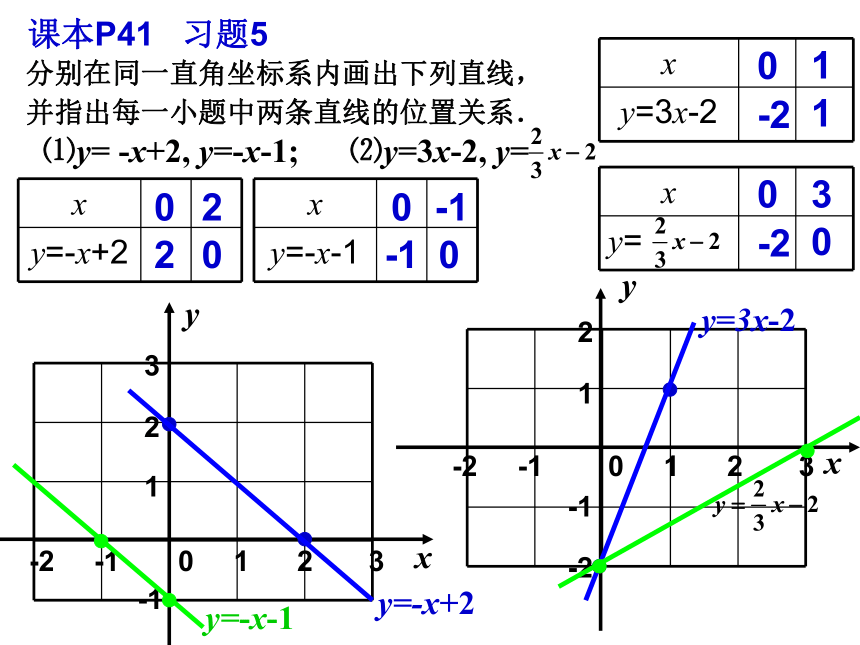
⑴y= -x+2, y=-x-1; ⑵y=3x-2, y=00-1-10022xy0 1 2 3-2 -1123-1xy0 1 2 3-2 -1-212-1y=-x+2y=-x-101-2103-20y=3x-2543210-1123-1-2y比较下列各对一次函数的图象有什么共同点,有什么不同点. 动画演示函数图象之间的关系:⑴当k相同 , b不同时:两直线平行直线y=kx+b可以看作由直线y=kx平移_____个单位而得到,当b>0时,向_____平移,当b<0时,向_____平移。 上下⑵当k不同 , b相同时:两直线相交于点(0,b)课本P37 练习1、2
练习册P41
变式例2(练习册P40 例)已知一次函数 .⑴若图象经过原点,求m的值; ⑵若图象平行于直线y=2x,求m的值;⑶若图象与y轴相交于正半轴,且交点与原点的距离为5个单位长度,求m的值. 解:依题意得 ⑴ 2m+1=0 ∴ m=-0.5⑵ m-1=2 ∴ m=3⑶ 2m+1=5 ∴ m=2y=kx+b(k≠0)的图象与性质:k:b:直线的倾斜程度(斜率)直线与y轴交点的位置⑴当k>0时,图象从左到右上升,y随x的增大而增大;⑵当k<0时,图象从左到右下降,y随x的增大而减小.⑴当b>0时,图象与y轴交于正半轴;⑵当b=0时,图象与y轴的交点为(0,0);⑶当b<0时,图象与y轴交于负半轴.动画演示课本P39 练习1
练习册P44
课堂练习 3、5、6例3(练习册P43 例1)已知一次函数 ,在下列条件下,求m,n的值或取值范围:⑴函数值y随x的增大而增大; ⑵函数图象经过原点;⑶函数图象与y轴的交点在x轴的下方. 解:依题意得 ⑴ m-3>0 ∴ m>3⑵ n+2=0 ∴ n=-2且m≠3⑶ n+2<0 ∴ n<-2且m≠3m-3≠0m-3≠0例4(练习册P45 7) 画出函数y=-2x+4的图象,结合图象回答下列问题:
⑴这个函数中,随着x的增大,y将增大还是减小?它的图象从左到右怎样变化?
⑵当x取何值时, y=0? ⑶当x取何值时, y<0?
⑷当010例5(练习册P43 例2)已知点(-3,m),(2,n)都在直线y=-3x+1上.试比较m和n的大小,你能想出几种不同的判断方法? 解:⑴ 依题意得m=10m=-3×(-3)+1n=-5n=-3×2+1∴ m>n⑵ ∵k=-3<0∴y随x的增大而减小又 ∵-3<2∴ m>n⑶ 画函数的草图-3m2n∴ m>n练习册P44
变式
课本P39 练习2k>ob=0b>0b<0b=0b>0b<0k<0一,三一,二,三一,三,四二,四一,二,四二,三,四当k>0时,y的值随x的增大而增大当k<0时,y的值随x的增大而减小y=kx+b(k≠0)图象的象限分布:练习册P44 2、4、7问题1中小明距北京的路程 s (千米)与在高速公里上行驶的时间t (时)之间的函数关系式是s=570-95t,试画出这个函数的图象. 例6(课本P38 例3)解:依题意得 t≥0 570-95t≥0 解得 t≥0 t≤6 ∴ 0≤t≤6005706画实际问题中的函数图象时,横、纵坐标可取不同的单位长度.此时一次函数的图象是一条线段.想想还有其他情形吗?课本P35、36 问题2 练习1、2、3、4y=50+12x(x是正整数)12627401 2 3 4 5 6 7 8 960708090100110120130x(个)y(元)此时一次函数的图象是一些离散孤立的点.3、某型号汽油的数量(L)与相应的金额(元)的关系如图所示,则这种汽油的单价是每升5.69元.y=5.69x(x≥0) 此时一次函数的图象是一条射线.
(1) y=2x与y=2x-3;
(2) y=2x+1与y= . 课本P37 例1010002-31.5-11212-1-2-3y=2xy=2x-3
(0,1)(-0.5,0)(0,1)(-2,0)12-1-212-1y=2x+1
1.求下列直线与x轴和y轴的交点,并在同一直角坐标系中画出它们的图象:课本P38 练习1(1) y=4x-1; (2)y=解:⑴令y=0得 4x-1=0 x=0.25∴直线与x轴的交点为(0.25,0)令x=0得 y=-1∴直线与y轴的交点为(0,-1)课本P41 习题5分别在同一直角坐标系内画出下列直线,并指出每一小题中两条直线的位置关系.
⑴y= -x+2, y=-x-1; ⑵y=3x-2, y=00-1-10022xy0 1 2 3-2 -1123-1xy0 1 2 3-2 -1-212-1y=-x+2y=-x-101-2103-20y=3x-2543210-1123-1-2y比较下列各对一次函数的图象有什么共同点,有什么不同点. 动画演示函数图象之间的关系:⑴当k相同 , b不同时:两直线平行直线y=kx+b可以看作由直线y=kx平移_____个单位而得到,当b>0时,向_____平移,当b<0时,向_____平移。 上下⑵当k不同 , b相同时:两直线相交于点(0,b)课本P37 练习1、2
练习册P41
变式例2(练习册P40 例)已知一次函数 .⑴若图象经过原点,求m的值; ⑵若图象平行于直线y=2x,求m的值;⑶若图象与y轴相交于正半轴,且交点与原点的距离为5个单位长度,求m的值. 解:依题意得 ⑴ 2m+1=0 ∴ m=-0.5⑵ m-1=2 ∴ m=3⑶ 2m+1=5 ∴ m=2y=kx+b(k≠0)的图象与性质:k:b:直线的倾斜程度(斜率)直线与y轴交点的位置⑴当k>0时,图象从左到右上升,y随x的增大而增大;⑵当k<0时,图象从左到右下降,y随x的增大而减小.⑴当b>0时,图象与y轴交于正半轴;⑵当b=0时,图象与y轴的交点为(0,0);⑶当b<0时,图象与y轴交于负半轴.动画演示课本P39 练习1
练习册P44
课堂练习 3、5、6例3(练习册P43 例1)已知一次函数 ,在下列条件下,求m,n的值或取值范围:⑴函数值y随x的增大而增大; ⑵函数图象经过原点;⑶函数图象与y轴的交点在x轴的下方. 解:依题意得 ⑴ m-3>0 ∴ m>3⑵ n+2=0 ∴ n=-2且m≠3⑶ n+2<0 ∴ n<-2且m≠3m-3≠0m-3≠0例4(练习册P45 7) 画出函数y=-2x+4的图象,结合图象回答下列问题:
⑴这个函数中,随着x的增大,y将增大还是减小?它的图象从左到右怎样变化?
⑵当x取何值时, y=0? ⑶当x取何值时, y<0?
⑷当0
变式
课本P39 练习2k>ob=0b>0b<0b=0b>0b<0k<0一,三一,二,三一,三,四二,四一,二,四二,三,四当k>0时,y的值随x的增大而增大当k<0时,y的值随x的增大而减小y=kx+b(k≠0)图象的象限分布:练习册P44 2、4、7问题1中小明距北京的路程 s (千米)与在高速公里上行驶的时间t (时)之间的函数关系式是s=570-95t,试画出这个函数的图象. 例6(课本P38 例3)解:依题意得 t≥0 570-95t≥0 解得 t≥0 t≤6 ∴ 0≤t≤6005706画实际问题中的函数图象时,横、纵坐标可取不同的单位长度.此时一次函数的图象是一条线段.想想还有其他情形吗?课本P35、36 问题2 练习1、2、3、4y=50+12x(x是正整数)12627401 2 3 4 5 6 7 8 960708090100110120130x(个)y(元)此时一次函数的图象是一些离散孤立的点.3、某型号汽油的数量(L)与相应的金额(元)的关系如图所示,则这种汽油的单价是每升5.69元.y=5.69x(x≥0) 此时一次函数的图象是一条射线.
