第十章平行线回顾与总结学案

本资料来自于资源最齐全的２１世纪教育网www.21cnjy.com
第十章平行线回顾与总结 学案
设计人：王庆平
学习目标：
1. 经历对本章所学知识回顾与思考的过程,将本章内容条理化,系统化。
2.通过对知识的疏理,进一步加深对所学概念的理解,进一步熟悉和掌握几何语言,能用语言说明几何图形.
3.使学生认识平面内两条直线的位置关系,在研究平行线时,能通过有关的角来判断直线平行和反映平行线的性质,理解平移的性质。
学习重、难点：
复习平面内两条直线的相交和平行的位置关系,以及相交平行的综合应用。
学习过程： 对顶角（性质）__________________
任务一、构建知识框架：
两直线相交 垂直 点到直线的距离。
相交直线
两条直线被第三条直线所截 同位角，内错角，同旁内角。
过直线外一点有且只有一条直线与已知直线平行。
_____________________,两直线平行。
两条直线平行的条件 _____________________,两直线平行。
平行直线
_____________________,两直线平行。
平行线的画法：1、_____2、______3、_____4、________.
两直线平行，_______________.
两直线平行的特征 两直线平行，_______________.
两直线平行，________________.
任务二、回忆重要概念：
1、平行线：_________________,不相交的两条直线。
2、两条平行线之间的距离： 。
任务三、辨认图形
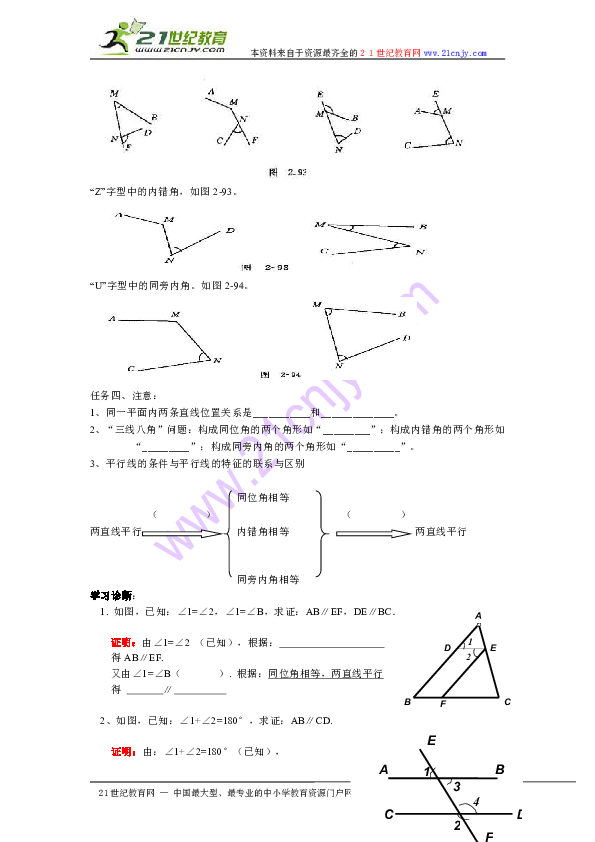
“F”型中的同位角。如图2-92。
“Z”字型中的内错角，如图2-93。
“U”字型中的同旁内角。如图2-94。
任务四、注意：
1、同一平面内两条直线位置关系是___________和______________。
2、“三线八角”问题：构成同位角的两个角形如“_________”；构成内错角的两个角形如“_________”；构成同旁内角的两个角形如“__________”。
3、平行线的条件与平行线的特征的联系与区别
同位角相等
（ ） （ ）
两直线平行 内错角相等 两直线平行
同旁内角相等
学习诊断：
1. 如图，已知：∠1=∠2，∠1=∠B，求证：AB∥EF，DE∥BC．
证明：由∠1=∠2 （已知），根据：
得AB∥EF.
又由∠1=∠B（ ）. 根据：同位角相等，两直线平行
得 ∥
2、如图，已知：∠1+∠2=180°，求证：AB∥CD.
证明：由：∠1+∠2=180°（已知），
∠1=∠3（对顶角相等）.
∠2=∠4（ ）
根据：等量代换
得：∠3+ =180°.
根据：同旁内角互补，两直线平行
得： ∥ .
3. 如图，已知：∠DAF=∠AFE，∠ADC+∠DCB=180°，求证：EF∥BC
证明：由：∠DAF=∠AFE （ ）
根据： .
得：AD∥ .
由：∠ADC+ =180°（已知）.
根据： .
得：AD∥ .
再根据： .
得：EF∥BC
4. 如图，已知：AC∥DE，∠1=∠2，试说明AB∥CD.
证明：由AC∥DE （已知）， 根据：两直线平行，内错角相等.
得∠ACD= .
又由∠1=∠2（已知）. 根据： .
得∠1=∠ACD . 再根据： .
得 ∥ .
【精讲点拨】
例1、（1）已知：AE平分∠BAC，CE平分∠ACD，∠1与∠2互余，AB∥CD吗？
说明理由.（判定的应用）
（2）如图：AB∥CD ，EF⊥CD，∠1=50°， 求∠2的度数.（性质的应用）
例2. 如图：AB∥CD，∠B=115°，∠C=45°，求∠BEC的度数．
例3 如图，已知∠C=70 ∠1=70 ，∠2=30 ，那么∠B=_______。
例4 在甲、乙两地之间要修一条笔直的公路，从甲地测得公路走向是北偏东30 。甲、乙两地同时开工，若干天后公路通，乙地所修公路的走向是南偏西_________度。
（例3题图） （例4题图）
【达标检测】
1. 已知：如图，AB∥CD，CE平分∠ACD，∠A=110°，则∠ECD的度数为（ ）
A. 110° B. 70° C. 55° D. 35°
2.如下左图所示，内错角共有( )
A.4对 B.6对 C.8对 D.10对
3. 如上右图，点E在BC的延长线上，在下列四个条件中，不能判定AB∥CD的是( )
A.∠1=∠2 B.∠B=∠DCE C.∠3=∠4 D.∠D+∠DAB=180°
4.下列说法正确的个数是( )
①同位角相等； ②过一点有且只有一条直线与已知直线垂直；
③过一点有且只有一条直线与已知直线平行;；④三条直线两两相交，总有三个交点； ⑤若a∥b，b∥c，则a∥c.
A.1个 B.2个 C.3个 D.4个
5、如图，AB∥CD，∠1+∠2+∠3=（ ）
A. 180° B. 360° C. 540° D. 720°
9. 画图题:（1）如下图(画AE⊥BC于E，AF⊥DC于F.
(2)画DG∥AC交BC的延长线于G.

21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网