数学中考压轴题精选及答案
图片预览



文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
连云港市2010年
1.如图,在平面直角坐标系中,O为坐标原点,⊙C的圆心坐标为(-2,-2),半径为.函数y=-x+2的图象与x轴交于点A,与y轴交于点B,点P为AB上一动点
(1)连接CO,求证:CO⊥AB;
(2)若△POA是等腰三角形,求点P的坐标;
(3)当直线PO与⊙C相切时,求∠POA的度数;当直线PO与⊙C相交时,设交点为E、F,点M为线段EF的中点,令PO=t,MO=s,求s与t之间的函数关系,并写出t的取值范围.
宿迁市2010
2.已知抛物线交轴于、,交轴于点,其顶点为.
(1)求、的值并写出抛物线的对称轴;
(2)连接,过点作直线交抛物线的对称轴于点.求证:四边形是等腰梯形;
(3)问Q抛物线上是否存在点,使得△OBQ的面积等于四边形的面积的?若存在,求出点的坐标;若不存在,请说明理由.
2010年无锡市
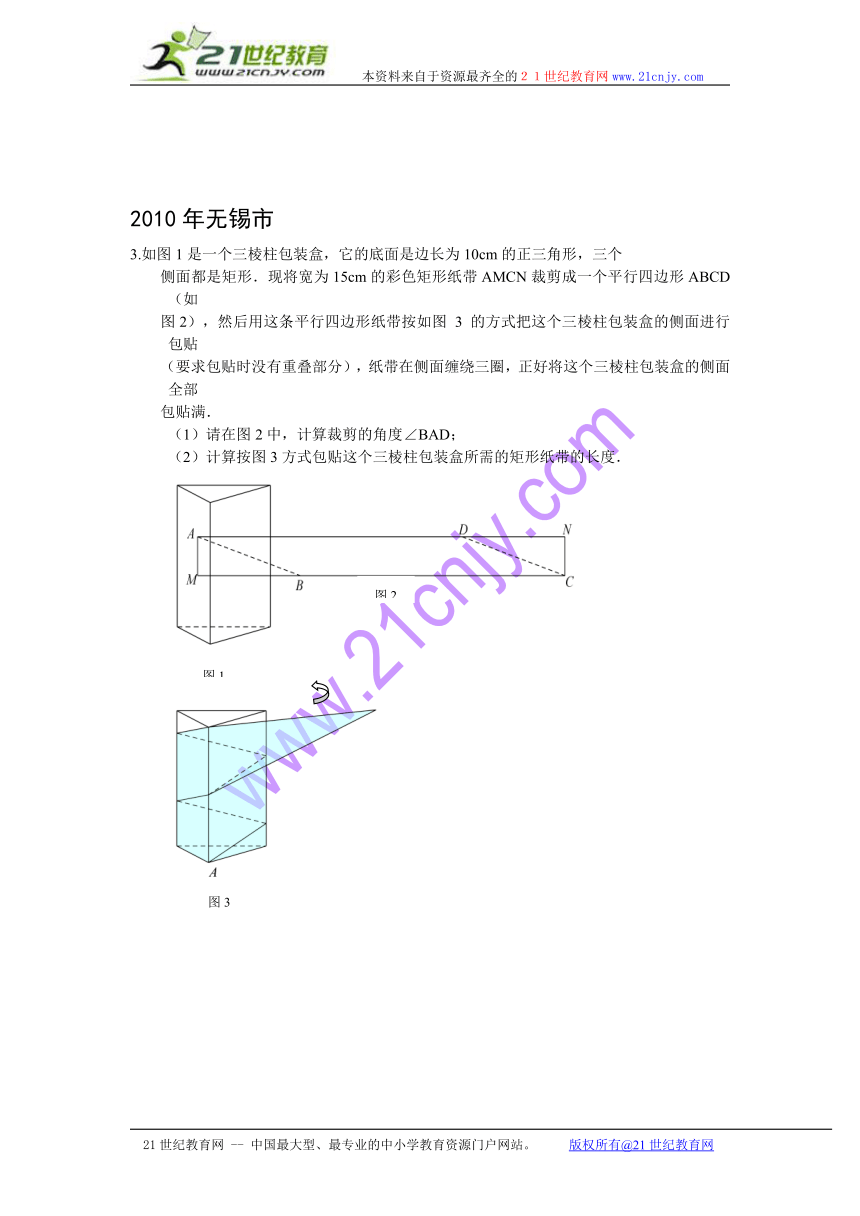
3.如图1是一个三棱柱包装盒,它的底面是边长为10cm的正三角形,三个
侧面都是矩形.现将宽为15cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如
图2),然后用这条平行四边形纸带按如图 3 的方式把这个三棱柱包装盒的侧面进行包贴
(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部
包贴满.
(1)请在图2中,计算裁剪的角度∠BAD;
(2)计算按图3方式包贴这个三棱柱包装盒所需的矩形纸带的长度.
2010年江苏省扬州市
4.在△ABC中,∠C=90°,AC=3,BC=4,CD是斜边AB上的高,点E在斜边AB上,过点E作直线与△ABC的直角边相交于点F,设AE=x,△AEF的面积为y.
(1)求线段AD的长;
(2)若EF⊥AB,当点E在线段AB上移动时,
①求y与x的函数关系式(写出自变量x的取值范围)
②当x取何值时,y有最大值?并求其最大值;
(3)若F在直角边AC上(点F与A、C两点均不重合),点E在斜边AB上移动,试问:是否存在直线EF将△ABC的周长和面积同时平分?若存在直线EF,求出x的值;若不存在直线EF,请说明理由.
2010年苏州市
5.如图,以A为顶点的抛物线与y轴交于点B.已知A、B两点的坐标分别为(3,0)、(0,4).
(1)求抛物线的解析式;
(2)设M(m,n)是抛物线上的一点(m、n为正整数),且它位于对称轴的右侧.若以M、B、O、A为顶点的四边形四条边的长度是四个连续的正整数,求点M的坐标;
(3)在(2)的条件下,试问:对于抛物线对称轴上的任意一点P,PA2+PB2+PM2>28是
否总成立 请说明理由.
大连市2010
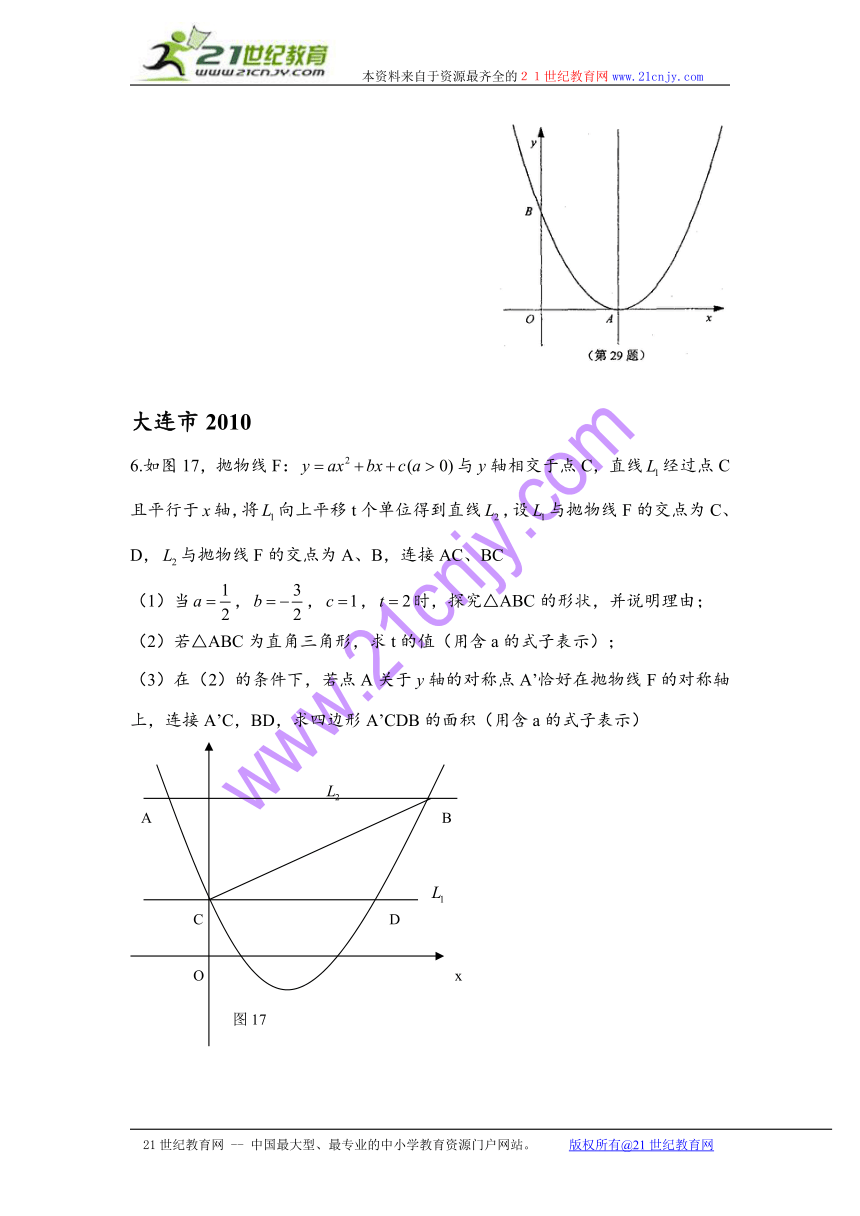
6.如图17,抛物线F:与轴相交于点C,直线经过点C且平行于轴,将向上平移t个单位得到直线,设与抛物线F的交点为C、D,与抛物线F的交点为A、B,连接AC、BC
(1)当,,,时,探究△ABC的形状,并说明理由;
(2)若△ABC为直角三角形,求t的值(用含a的式子表示);
(3)在(2)的条件下,若点A关于轴的对称点A’恰好在抛物线F的对称轴上,连接A’C,BD,求四边形A’CDB的面积(用含a的式子表示)
2010年青岛市
7.已知:把Rt△ABC和Rt△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠ACB = ∠EDF = 90°,∠DEF = 45°,AC = 8 cm,BC = 6 cm,EF = 9 cm.
如图(2),△DEF从图(1)的位置出发,以1 cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2 cm/s的速度沿BA向点A匀速移动.当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移动.DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5).解答下列问题:
(1)当t为何值时,点A在线段PQ的垂直平分线上?
(2)连接PE,设四边形APEC的面积为y(cm2),求y与t之间的函数关系式;是否存在某一时刻t,使面积y最小?若存在,求出y的最小值;若不存在,说明理由.
(3)是否存在某一时刻t,使P、Q、F三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由.(图(3)供同学们做题使用)
解:(1)
(2)
(3)
2010年烟台市
8.如图,已知抛物线y=x2+bx-3a过点A(1,0),B(0,-3),与x轴交于另一点C。
(1)求抛物线的解析式;
(2)若在第三象限的抛物线上存在点P,使△PBC为以点B为直角顶点的直角三角形,求点P的坐标;
(3)在(2)的条件下,在抛物线上是否存在一点Q,使以P,Q,B,C为顶点的四边形为直角梯形?若存在,请求出点Q的坐标;若不存在,请说明理由。
2010年上海市
9.如图9,在Rt△ABC中,∠ACB=90°.半径为1的圆A与边AB相交于点D,与边AC相交于点E,连结DE并延长,与线段BC的延长线交于点P.
(1)当∠B=30°时,连结AP,若△AEP与△BDP相似,求CE的长;
(2)若CE=2,BD=BC,求∠BPD的正切值;
(3)若,设CE=x,△ABC的周长为y,求y关于x的函数关系式.
图9 图10(备用) 图11(备用)
眉山市2010
10.如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(,0)、(0,4),抛物线经过B点,且顶点在直线上.
(1)求抛物线对应的函数关系式;
(2)若△DCE是由△ABO沿x轴向右平移得到的,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由;
(3)若M点是CD所在直线下方该抛物线上的一个动点,过点M作MN平行于y轴交CD于点N.设点M的横坐标为t,MN的长度为l.求l与t之间的函数关系式,并求l取最大值时,点M的坐标.
参考答案
连云港市2010年
1.解:(1)延长CO交AB于D,过点C作CG⊥x轴于点G.
因为直线AB的函数关系式是y=-x+2,所以易得A(2,0),B(0,2)
所以AO=BO=2
又因为∠AOB=90°,所以∠DAO=45°(1分)
因为C(-2,-2),所以CG=OG=2
所以∠COG=45°,∠AOD=45°(2分)
所以∠ODA=90°,
所以OD⊥AB,即CO⊥AB(3分)
(2)要使△POA为等腰三角形
1 当OP=OA时,此时点P与点B重合,所以点P坐标为(0,2);
2 当PO=PA时,由∠OAB=450,所以点P恰好是AB的中点,所以点P坐标为(1,1);
3 当AP=AO时,则AP=2,过点P作PH⊥OA交于点H,在Rt△APH中,易得PH=AH= ,所以OH=2- ,所以点坐标为(2- , )(7分)
(3)当直线PO与⊙O相切时,设切点为K,连接CK,则CK⊥OK
由点C的坐标为(-2,-2),易得CO=2 ,
又因为⊙C的半径为 ,所以∠COK=30°,
所以∠POD=30°,又∠AOD=45°,所以∠POA=75°
同理可求出∠POA的另一个值为15°
所以∠POA等于75°或15°(10分)
因为M为EF的中点,所以CM⊥EF
又因为∠COM=∠POD.CO⊥AB
所以△COM∽△POD
所以 = ,即MO PO=CO DO
因为PO=t,MO=s,CO=2 ,DO= ,所以st=4.
当PO过圆心C时,MO=CO=2 ,PO=DO= ,即MO PO=4,也满足st=4.所以s= .( ).
宿迁市2010年
2.(1)求出:,,抛物线的对称轴为:x=2 ………………3分
(2) 抛物线的解析式为,易得C点坐标为(0,3),D点坐标为(2,-1)
设抛物线的对称轴DE交x轴于点F,易得F点坐标为(2,0),连接OD,DB,BE
∵OBC是等腰直角三角形,DFB也是等腰直角三角形,E点坐标为(2,2),
∴∠BOE= ∠OBD= ∴OE∥BD
∴四边形ODBE是梯形 ………………5分
在和中,
OD= ,BE=
∴OD= BE
∴四边形ODBE是等腰梯形 ………………7分
(3) 存在, ………………8分
由题意得: ………………9分
设点Q坐标为(x,y),
由题意得:=
∴
当y=1时,即,∴ , ,
∴Q点坐标为(2+,1)或(2-,1) ………………11分
当y=-1时,即, ∴x=2,
∴Q点坐标为(2,-1)
综上所述,抛物线上存在三点Q(2+,1),Q (2-,1) ,Q(2,-1)
使得=. ………………12分
无锡市2010年
3.(1)由图2的包贴方法知:AB的长等于三棱柱的底边周长,∴AB=30
∵纸带宽为15,∴sin∠DAB=sin∠ABM=,∴∠DAB=30°.
(2)在图3中,将三棱柱沿过点A的侧棱剪开,得到如图甲的侧面展开图,
将图甲种的△ABE向左平移30cm,△CDF向右平移30cm,拼成如图乙中的平行四边形ABCD,
此平行四边形即为图2中的平行四边形ABCD
由题意得,知:BC=BE+CE=2CE=2×,
∴所需矩形纸带的长为MB+BC=30·cos30°+=cm.
2010年江苏扬州市
4. 解:(1)因为AC=3,BC=4,
所以AB=5
因为AC· BC=AB· CD
所以CD=,
在Rt△ACD中,根据勾股定理知AD=
(2)①当0<x≤时,
因为EF∥CD,
所以△AEF∽△ADC
所以=
即EF=x
所以y= ·x·x=x2
当<x<5时,
易得△BEF∽△BDC,同理可求得EF=(5—x)
所以, y= ·x·(5—x)=—x2+x
②当0<x≤时,y随时x的增大而增大,y=x2≤
即当0<x≤时,y的最大值为
当<x<5时,y=—x2+=-(x—)2+
因为—<0,
所以,当x=时,y的最大值为
因为<,
所以,当x=时,y取最大值为
(3)假设存在
当0<x≤5时,AF=6—x,
所以,0<6—x<3,
所以,3<x<6
所以,3<x≤5。
作FG⊥AB于点G
由△AFG∽△ACD,可得,
=
所以,FG=(6—x)
所以,S△AEF=·x·(6—x)= —x2+x
所以—x2+x=3,即2 x2-12x+15=0
解之得x1= x2=
因为3<x≤5,
所以,x1=符合题意
因为x2=<3
所以x2不合题意,应舍去。
所以存在这样的直线EF,此时x=
2010年苏州市
5.
大连市2010年
6.
2010年青岛市
7.解:(1)∵点A在线段PQ的垂直平分线上,
∴AP = AQ.
∵∠DEF = 45°,∠ACB = 90°,∠DEF+∠ACB+∠EQC = 180°,
∴∠EQC = 45°.
∴∠DEF =∠EQC.
∴CE = CQ.
由题意知:CE = t,BP =2 t,
∴CQ = t.
∴AQ = 8-t.
在Rt△ABC中,由勾股定理得:AB = 10 cm .
则AP = 10-2 t.
∴10-2 t = 8-t.
解得:t = 2.
答:当t = 2 s时,点A在线段PQ的垂直平分线上. 4分
(2)过P作,交BE于M,
∴.
在Rt△ABC和Rt△BPM中,,
∴ . ∴PM = .
∵BC = 6 cm,CE = t, ∴ BE = 6-t.
∴y = S△ABC-S△BPE =-= -
= = .
∵,∴抛物线开口向上.
∴当t = 3时,y最小=.
答:当t = 3s时,四边形APEC的面积最小,最小面积为cm2. 8分
(3)假设存在某一时刻t,使点P、Q、F三点在同一条直线上.
过P作,交AC于N,
∴.
∵,∴△PAN ∽△BAC.
∴.
∴.
∴,.
∵NQ = AQ-AN,
∴NQ = 8-t-() = .
∵∠ACB = 90°,B、C(E)、F在同一条直线上,
∴∠QCF = 90°,∠QCF = ∠PNQ.
∵∠FQC = ∠PQN,
∴△QCF∽△QNP .
∴ . ∴ .
∵ ∴
解得:t = 1.
答:当t = 1s,点P、Q、F三点在同一条直线上. 12分
2010年烟台市
2010年上海市
9.(1)解:∵∠B=30°∠ACB=90°∴∠BAC=60°
∵AD=AE ∴∠AED=60°=∠CEP
∴∠EPC=30°
∴三角形BDP为等腰三角形
∵△AEP与△BDP相似
∴∠EAP=∠EPA=∠DBP=∠DPB=30°
∴AE=EP=1
∴在RT△ECP中,EC=EP=
(2)过点D作DQ⊥AC于点Q,且设AQ=a,BD=x
∵AE=1,EC=2
∴QC=3-a
∵∠ACB=90°
∴△ADQ与△ABC相似
∴
即,∴
∵在RT△ADQ中
∵
∴
解之得x=4,即BC=4
过点C作CF//DP
∴△ADE与△AFC相似,
∴,即AF=AC,即DF=EC=2,
∴BF=DF=2
∵△BFC与△BDP相似
∴,即:BC=CP=4
∴tan∠BPD=
(3)过D点作DQ⊥AC于点Q,则△DQE与△PCE相似,设AQ=a,则QE=1-a
∴且
∴
∵在Rt△ADQ中,据勾股定理得:
即:,解之得
∵△ADQ与△ABC相似
∴
∴
∴三角形ABC的周长
即:,其中x>0
2010年眉山市
10. 解:(1)由题意,可设所求抛物线对应的函数关系式为 …(1分)
∴
∴ ……………………………………………………………(3分)
∴所求函数关系式为: …………(4分)
(2)在Rt△ABO中,OA=3,OB=4,
∴
∵四边形ABCD是菱形
∴BC=CD=DA=AB=5 ……………………………………(5分)
∴C、D两点的坐标分别是(5,4)、(2,0). …………(6分)
当时,
当时,
∴点C和点D在所求抛物线上. …………………………(7分)
(3)设直线CD对应的函数关系式为,则
解得:.
∴ ………(9分)
∵MN∥y轴,M点的横坐标为t,
∴N点的横坐标也为t.
则, ,……………………(10分)
∴
∵, ∴当时,,
此时点M的坐标为(,). ………………………………(12分)
AD
BAD
x
P
O
·
·
CFEBAD
y
图1
图2
图3
A
B
C
D
A
B
C
D
备用图
O
C
A
B
D
x
图17
A
D
B
C
F
(
E
)
图(1)
A
D
B
C
F
E
图(2)
P
Q
A
B
C
图(3)
E
F
Q1
Q3
Q2
图甲
图乙
图(2)
Q
A
D
B
C
F
E
P
M
C
E
A
D
B
F
图(3)
P
Q
N
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
连云港市2010年
1.如图,在平面直角坐标系中,O为坐标原点,⊙C的圆心坐标为(-2,-2),半径为.函数y=-x+2的图象与x轴交于点A,与y轴交于点B,点P为AB上一动点
(1)连接CO,求证:CO⊥AB;
(2)若△POA是等腰三角形,求点P的坐标;
(3)当直线PO与⊙C相切时,求∠POA的度数;当直线PO与⊙C相交时,设交点为E、F,点M为线段EF的中点,令PO=t,MO=s,求s与t之间的函数关系,并写出t的取值范围.
宿迁市2010
2.已知抛物线交轴于、,交轴于点,其顶点为.
(1)求、的值并写出抛物线的对称轴;
(2)连接,过点作直线交抛物线的对称轴于点.求证:四边形是等腰梯形;
(3)问Q抛物线上是否存在点,使得△OBQ的面积等于四边形的面积的?若存在,求出点的坐标;若不存在,请说明理由.
2010年无锡市
3.如图1是一个三棱柱包装盒,它的底面是边长为10cm的正三角形,三个
侧面都是矩形.现将宽为15cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如
图2),然后用这条平行四边形纸带按如图 3 的方式把这个三棱柱包装盒的侧面进行包贴
(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部
包贴满.
(1)请在图2中,计算裁剪的角度∠BAD;
(2)计算按图3方式包贴这个三棱柱包装盒所需的矩形纸带的长度.
2010年江苏省扬州市
4.在△ABC中,∠C=90°,AC=3,BC=4,CD是斜边AB上的高,点E在斜边AB上,过点E作直线与△ABC的直角边相交于点F,设AE=x,△AEF的面积为y.
(1)求线段AD的长;
(2)若EF⊥AB,当点E在线段AB上移动时,
①求y与x的函数关系式(写出自变量x的取值范围)
②当x取何值时,y有最大值?并求其最大值;
(3)若F在直角边AC上(点F与A、C两点均不重合),点E在斜边AB上移动,试问:是否存在直线EF将△ABC的周长和面积同时平分?若存在直线EF,求出x的值;若不存在直线EF,请说明理由.
2010年苏州市
5.如图,以A为顶点的抛物线与y轴交于点B.已知A、B两点的坐标分别为(3,0)、(0,4).
(1)求抛物线的解析式;
(2)设M(m,n)是抛物线上的一点(m、n为正整数),且它位于对称轴的右侧.若以M、B、O、A为顶点的四边形四条边的长度是四个连续的正整数,求点M的坐标;
(3)在(2)的条件下,试问:对于抛物线对称轴上的任意一点P,PA2+PB2+PM2>28是
否总成立 请说明理由.
大连市2010
6.如图17,抛物线F:与轴相交于点C,直线经过点C且平行于轴,将向上平移t个单位得到直线,设与抛物线F的交点为C、D,与抛物线F的交点为A、B,连接AC、BC
(1)当,,,时,探究△ABC的形状,并说明理由;
(2)若△ABC为直角三角形,求t的值(用含a的式子表示);
(3)在(2)的条件下,若点A关于轴的对称点A’恰好在抛物线F的对称轴上,连接A’C,BD,求四边形A’CDB的面积(用含a的式子表示)
2010年青岛市
7.已知:把Rt△ABC和Rt△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠ACB = ∠EDF = 90°,∠DEF = 45°,AC = 8 cm,BC = 6 cm,EF = 9 cm.
如图(2),△DEF从图(1)的位置出发,以1 cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2 cm/s的速度沿BA向点A匀速移动.当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移动.DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5).解答下列问题:
(1)当t为何值时,点A在线段PQ的垂直平分线上?
(2)连接PE,设四边形APEC的面积为y(cm2),求y与t之间的函数关系式;是否存在某一时刻t,使面积y最小?若存在,求出y的最小值;若不存在,说明理由.
(3)是否存在某一时刻t,使P、Q、F三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由.(图(3)供同学们做题使用)
解:(1)
(2)
(3)
2010年烟台市
8.如图,已知抛物线y=x2+bx-3a过点A(1,0),B(0,-3),与x轴交于另一点C。
(1)求抛物线的解析式;
(2)若在第三象限的抛物线上存在点P,使△PBC为以点B为直角顶点的直角三角形,求点P的坐标;
(3)在(2)的条件下,在抛物线上是否存在一点Q,使以P,Q,B,C为顶点的四边形为直角梯形?若存在,请求出点Q的坐标;若不存在,请说明理由。
2010年上海市
9.如图9,在Rt△ABC中,∠ACB=90°.半径为1的圆A与边AB相交于点D,与边AC相交于点E,连结DE并延长,与线段BC的延长线交于点P.
(1)当∠B=30°时,连结AP,若△AEP与△BDP相似,求CE的长;
(2)若CE=2,BD=BC,求∠BPD的正切值;
(3)若,设CE=x,△ABC的周长为y,求y关于x的函数关系式.
图9 图10(备用) 图11(备用)
眉山市2010
10.如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(,0)、(0,4),抛物线经过B点,且顶点在直线上.
(1)求抛物线对应的函数关系式;
(2)若△DCE是由△ABO沿x轴向右平移得到的,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由;
(3)若M点是CD所在直线下方该抛物线上的一个动点,过点M作MN平行于y轴交CD于点N.设点M的横坐标为t,MN的长度为l.求l与t之间的函数关系式,并求l取最大值时,点M的坐标.
参考答案
连云港市2010年
1.解:(1)延长CO交AB于D,过点C作CG⊥x轴于点G.
因为直线AB的函数关系式是y=-x+2,所以易得A(2,0),B(0,2)
所以AO=BO=2
又因为∠AOB=90°,所以∠DAO=45°(1分)
因为C(-2,-2),所以CG=OG=2
所以∠COG=45°,∠AOD=45°(2分)
所以∠ODA=90°,
所以OD⊥AB,即CO⊥AB(3分)
(2)要使△POA为等腰三角形
1 当OP=OA时,此时点P与点B重合,所以点P坐标为(0,2);
2 当PO=PA时,由∠OAB=450,所以点P恰好是AB的中点,所以点P坐标为(1,1);
3 当AP=AO时,则AP=2,过点P作PH⊥OA交于点H,在Rt△APH中,易得PH=AH= ,所以OH=2- ,所以点坐标为(2- , )(7分)
(3)当直线PO与⊙O相切时,设切点为K,连接CK,则CK⊥OK
由点C的坐标为(-2,-2),易得CO=2 ,
又因为⊙C的半径为 ,所以∠COK=30°,
所以∠POD=30°,又∠AOD=45°,所以∠POA=75°
同理可求出∠POA的另一个值为15°
所以∠POA等于75°或15°(10分)
因为M为EF的中点,所以CM⊥EF
又因为∠COM=∠POD.CO⊥AB
所以△COM∽△POD
所以 = ,即MO PO=CO DO
因为PO=t,MO=s,CO=2 ,DO= ,所以st=4.
当PO过圆心C时,MO=CO=2 ,PO=DO= ,即MO PO=4,也满足st=4.所以s= .( ).
宿迁市2010年
2.(1)求出:,,抛物线的对称轴为:x=2 ………………3分
(2) 抛物线的解析式为,易得C点坐标为(0,3),D点坐标为(2,-1)
设抛物线的对称轴DE交x轴于点F,易得F点坐标为(2,0),连接OD,DB,BE
∵OBC是等腰直角三角形,DFB也是等腰直角三角形,E点坐标为(2,2),
∴∠BOE= ∠OBD= ∴OE∥BD
∴四边形ODBE是梯形 ………………5分
在和中,
OD= ,BE=
∴OD= BE
∴四边形ODBE是等腰梯形 ………………7分
(3) 存在, ………………8分
由题意得: ………………9分
设点Q坐标为(x,y),
由题意得:=
∴
当y=1时,即,∴ , ,
∴Q点坐标为(2+,1)或(2-,1) ………………11分
当y=-1时,即, ∴x=2,
∴Q点坐标为(2,-1)
综上所述,抛物线上存在三点Q(2+,1),Q (2-,1) ,Q(2,-1)
使得=. ………………12分
无锡市2010年
3.(1)由图2的包贴方法知:AB的长等于三棱柱的底边周长,∴AB=30
∵纸带宽为15,∴sin∠DAB=sin∠ABM=,∴∠DAB=30°.
(2)在图3中,将三棱柱沿过点A的侧棱剪开,得到如图甲的侧面展开图,
将图甲种的△ABE向左平移30cm,△CDF向右平移30cm,拼成如图乙中的平行四边形ABCD,
此平行四边形即为图2中的平行四边形ABCD
由题意得,知:BC=BE+CE=2CE=2×,
∴所需矩形纸带的长为MB+BC=30·cos30°+=cm.
2010年江苏扬州市
4. 解:(1)因为AC=3,BC=4,
所以AB=5
因为AC· BC=AB· CD
所以CD=,
在Rt△ACD中,根据勾股定理知AD=
(2)①当0<x≤时,
因为EF∥CD,
所以△AEF∽△ADC
所以=
即EF=x
所以y= ·x·x=x2
当<x<5时,
易得△BEF∽△BDC,同理可求得EF=(5—x)
所以, y= ·x·(5—x)=—x2+x
②当0<x≤时,y随时x的增大而增大,y=x2≤
即当0<x≤时,y的最大值为
当<x<5时,y=—x2+=-(x—)2+
因为—<0,
所以,当x=时,y的最大值为
因为<,
所以,当x=时,y取最大值为
(3)假设存在
当0<x≤5时,AF=6—x,
所以,0<6—x<3,
所以,3<x<6
所以,3<x≤5。
作FG⊥AB于点G
由△AFG∽△ACD,可得,
=
所以,FG=(6—x)
所以,S△AEF=·x·(6—x)= —x2+x
所以—x2+x=3,即2 x2-12x+15=0
解之得x1= x2=
因为3<x≤5,
所以,x1=符合题意
因为x2=<3
所以x2不合题意,应舍去。
所以存在这样的直线EF,此时x=
2010年苏州市
5.
大连市2010年
6.
2010年青岛市
7.解:(1)∵点A在线段PQ的垂直平分线上,
∴AP = AQ.
∵∠DEF = 45°,∠ACB = 90°,∠DEF+∠ACB+∠EQC = 180°,
∴∠EQC = 45°.
∴∠DEF =∠EQC.
∴CE = CQ.
由题意知:CE = t,BP =2 t,
∴CQ = t.
∴AQ = 8-t.
在Rt△ABC中,由勾股定理得:AB = 10 cm .
则AP = 10-2 t.
∴10-2 t = 8-t.
解得:t = 2.
答:当t = 2 s时,点A在线段PQ的垂直平分线上. 4分
(2)过P作,交BE于M,
∴.
在Rt△ABC和Rt△BPM中,,
∴ . ∴PM = .
∵BC = 6 cm,CE = t, ∴ BE = 6-t.
∴y = S△ABC-S△BPE =-= -
= = .
∵,∴抛物线开口向上.
∴当t = 3时,y最小=.
答:当t = 3s时,四边形APEC的面积最小,最小面积为cm2. 8分
(3)假设存在某一时刻t,使点P、Q、F三点在同一条直线上.
过P作,交AC于N,
∴.
∵,∴△PAN ∽△BAC.
∴.
∴.
∴,.
∵NQ = AQ-AN,
∴NQ = 8-t-() = .
∵∠ACB = 90°,B、C(E)、F在同一条直线上,
∴∠QCF = 90°,∠QCF = ∠PNQ.
∵∠FQC = ∠PQN,
∴△QCF∽△QNP .
∴ . ∴ .
∵ ∴
解得:t = 1.
答:当t = 1s,点P、Q、F三点在同一条直线上. 12分
2010年烟台市
2010年上海市
9.(1)解:∵∠B=30°∠ACB=90°∴∠BAC=60°
∵AD=AE ∴∠AED=60°=∠CEP
∴∠EPC=30°
∴三角形BDP为等腰三角形
∵△AEP与△BDP相似
∴∠EAP=∠EPA=∠DBP=∠DPB=30°
∴AE=EP=1
∴在RT△ECP中,EC=EP=
(2)过点D作DQ⊥AC于点Q,且设AQ=a,BD=x
∵AE=1,EC=2
∴QC=3-a
∵∠ACB=90°
∴△ADQ与△ABC相似
∴
即,∴
∵在RT△ADQ中
∵
∴
解之得x=4,即BC=4
过点C作CF//DP
∴△ADE与△AFC相似,
∴,即AF=AC,即DF=EC=2,
∴BF=DF=2
∵△BFC与△BDP相似
∴,即:BC=CP=4
∴tan∠BPD=
(3)过D点作DQ⊥AC于点Q,则△DQE与△PCE相似,设AQ=a,则QE=1-a
∴且
∴
∵在Rt△ADQ中,据勾股定理得:
即:,解之得
∵△ADQ与△ABC相似
∴
∴
∴三角形ABC的周长
即:,其中x>0
2010年眉山市
10. 解:(1)由题意,可设所求抛物线对应的函数关系式为 …(1分)
∴
∴ ……………………………………………………………(3分)
∴所求函数关系式为: …………(4分)
(2)在Rt△ABO中,OA=3,OB=4,
∴
∵四边形ABCD是菱形
∴BC=CD=DA=AB=5 ……………………………………(5分)
∴C、D两点的坐标分别是(5,4)、(2,0). …………(6分)
当时,
当时,
∴点C和点D在所求抛物线上. …………………………(7分)
(3)设直线CD对应的函数关系式为,则
解得:.
∴ ………(9分)
∵MN∥y轴,M点的横坐标为t,
∴N点的横坐标也为t.
则, ,……………………(10分)
∴
∵, ∴当时,,
此时点M的坐标为(,). ………………………………(12分)
AD
BAD
x
P
O
·
·
CFEBAD
y
图1
图2
图3
A
B
C
D
A
B
C
D
备用图
O
C
A
B
D
x
图17
A
D
B
C
F
(
E
)
图(1)
A
D
B
C
F
E
图(2)
P
Q
A
B
C
图(3)
E
F
Q1
Q3
Q2
图甲
图乙
图(2)
Q
A
D
B
C
F
E
P
M
C
E
A
D
B
F
图(3)
P
Q
N
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
