8.5相似三角形的判断2学案

8.5相似三角形的判断方法2学案
单县终兴中学 编写人 王敏 吴新峰 审阅人 吴吉杰
一学习目标：
1掌握三角形相似的判定方法2，并能灵活应用解决问题。
2 通过实验探究两个三角形相似的判定方法，培养探究能力。
二自主预习：
相似 三角形判定方法1：
三自主预习：
相似三角形的判断方法2
（1）内容：如果一个三角形的两条边与另一个三角形的 两边对应 ，并且
相等，那么这两个三角形相似。
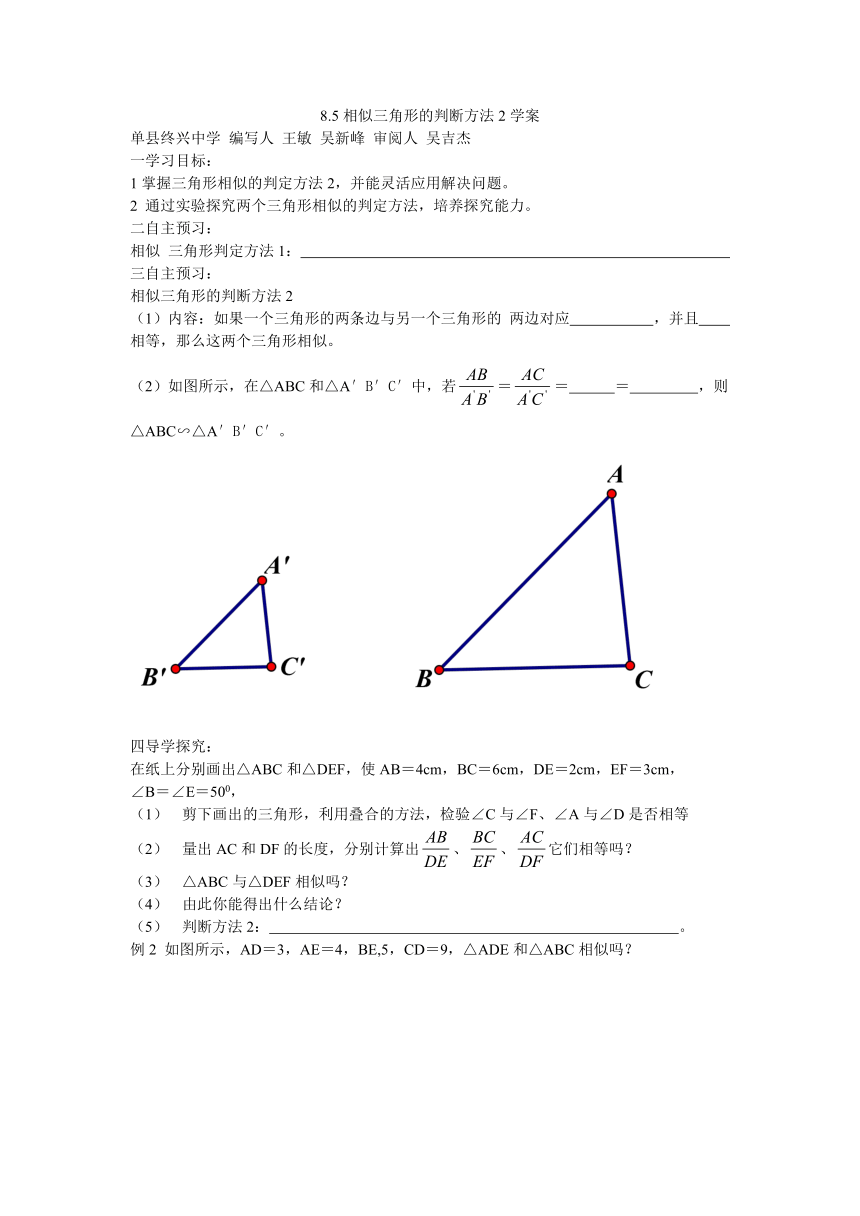
（2）如图所示，在△ABC和△A′B′C′中，若＝＝ ＝ ，则
△ABC∽△A′B′C′。
四导学探究：
在纸上分别画出△ABC和△DEF，使AB＝4cm，BC＝6cm，DE＝2cm，EF＝3cm，
∠B＝∠E＝500，
（1） 剪下画出的三角形，利用叠合的方法，检验∠C与∠F、∠A与∠D是否相等
（2） 量出AC和DF的长度，分别计算出、、它们相等吗？
（3） △ABC与△DEF相似吗？
（4） 由此你能得出什么结论？
（5） 判断方法2： 。
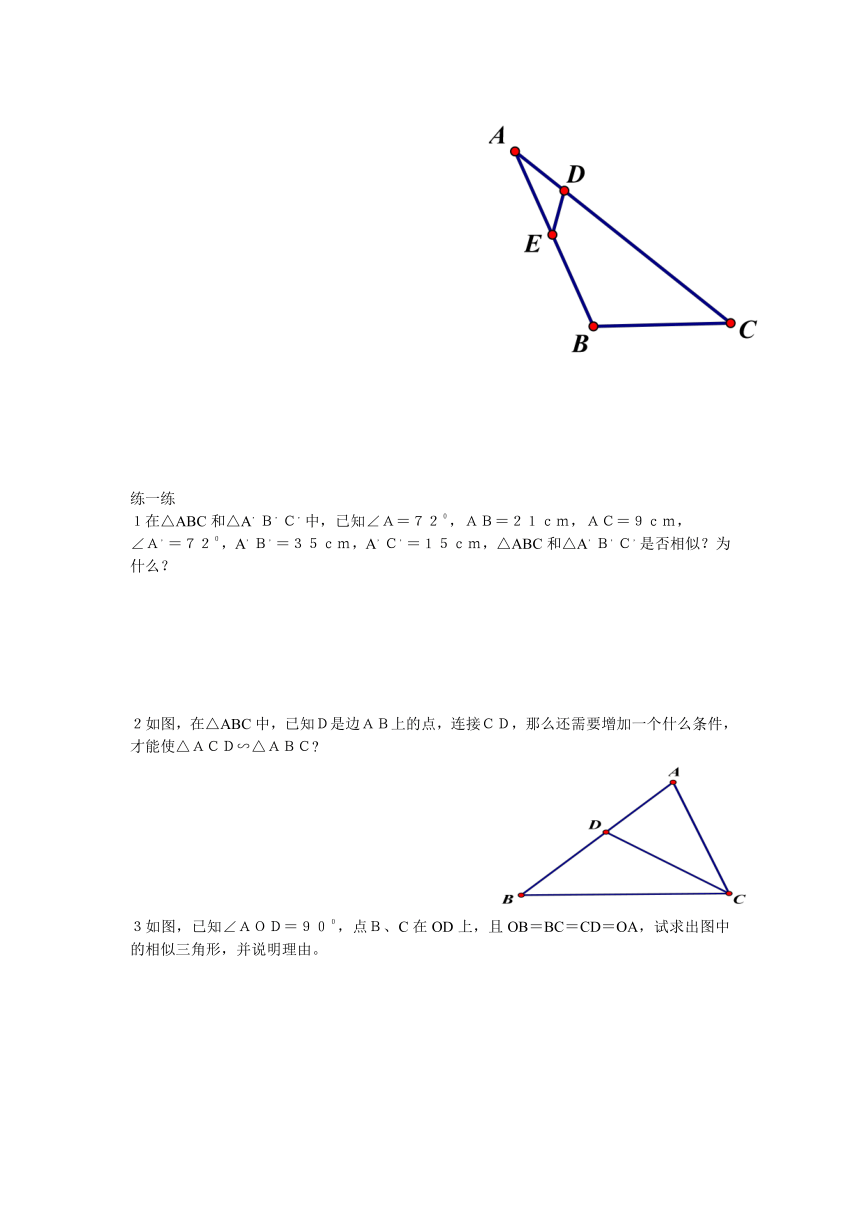
例2 如图所示，AD＝3，AE＝4，BE,5，CD＝9，△ADE和△ABC相似吗？
练一练
１在△ABC和△A，Ｂ，Ｃ，中，已知∠Ａ＝７２０，ＡＢ＝２１ｃｍ，ＡＣ＝９ｃｍ，
∠Ａ，＝７２０，A，Ｂ，＝３５ｃｍ，A，Ｃ，＝１５ｃｍ，△ABC和△A，Ｂ，Ｃ，是否相似？为什么？
２如图，在△ABC中，已知Ｄ是边ＡＢ上的点，连接ＣＤ，那么还需要增加一个什么条件，才能使△ＡＣＤ∽△ＡＢＣ
３如图，已知∠ＡＯＤ＝９００，点Ｂ、C在OD上，且OB＝BC＝CD＝OA，试求出图中的相似三角形，并说明理由。
4如图，在△ABC中，点D在BC上，∠BAC＝∠ADC,AC＝8，BC＝16，求CD的长。
五 当堂达标
1 如图，在4×4的正方形方格中，⊿ABC和⊿DEF的顶点都在边长为1的小正方形的顶点上，（1）填空：∠ABC= ，BC= (2)判断⊿ABC和⊿DEF是否相似，并说明你的结论。
2 如图，给出下列条件：（1）∠B=∠ACD(2) ∠ADC=∠ACB(3)= （4）AC2=AD·AB,其中能够单独判断⊿ABC∽⊿ACD的个数为（ ）A 1 B 2 C 3 D 4
3 如果一个直角三角形的两条边长分别是6和8，另一个与它相似的直角三角形边长分别是3和4及x，那么x的值（ ）
A 只有1个 B 可以有2个 C 有2个以上但有限 D 有无数个
4如图，正方形ABCD的边长是2，BE=CE,NN=1，线段MN的两端在CD,AD上滑动，当DM=
时，⊿ABE与以D,M,N为顶点的三角形相似
5如上图，在⊿ABC和⊿ADE中，∠BAD=∠CAE, ∠ABC=∠ADE,(1)写出图中两对相似三角形（不得添加字母和线）（2）请分析说明两对三角形相似的理由
六 能力提升：
1. 已知△ABC。
画一个△A，Ｂ，Ｃ，，使它与△ABC相似，并使△A，Ｂ，Ｃ，与△ABC的对应边的比为2:3 。
2 (2010.浙江杭州)如图，AB＝3AC,BD＝3AE,又BD∥AC,点B、A、E在同一条直线上。
（1）试说明△ABD∽△CAE;
(2)如果AC＝BD,AD＝2BD,设BD＝a，求BC的长。