8.5相似三角形的判定1学案

8.5怎样判定三角形相似学案一
一 学习目标：
1探索并掌握三角形的判断方法1，并运用 三角形相似的判定方法解决问题。
2历经探索两个三角形相似的判定方法的过程，进一步提高探究交流的能力，养成动手、动脑的习惯 。
二 知识回顾：
如果一个三角 形的三个角与另一个三角形的三个角 ，并且它们的各边对应 ，那么这两个三角形叫做相似三角形。
三自主预习：
三角形相似的判定方法1：
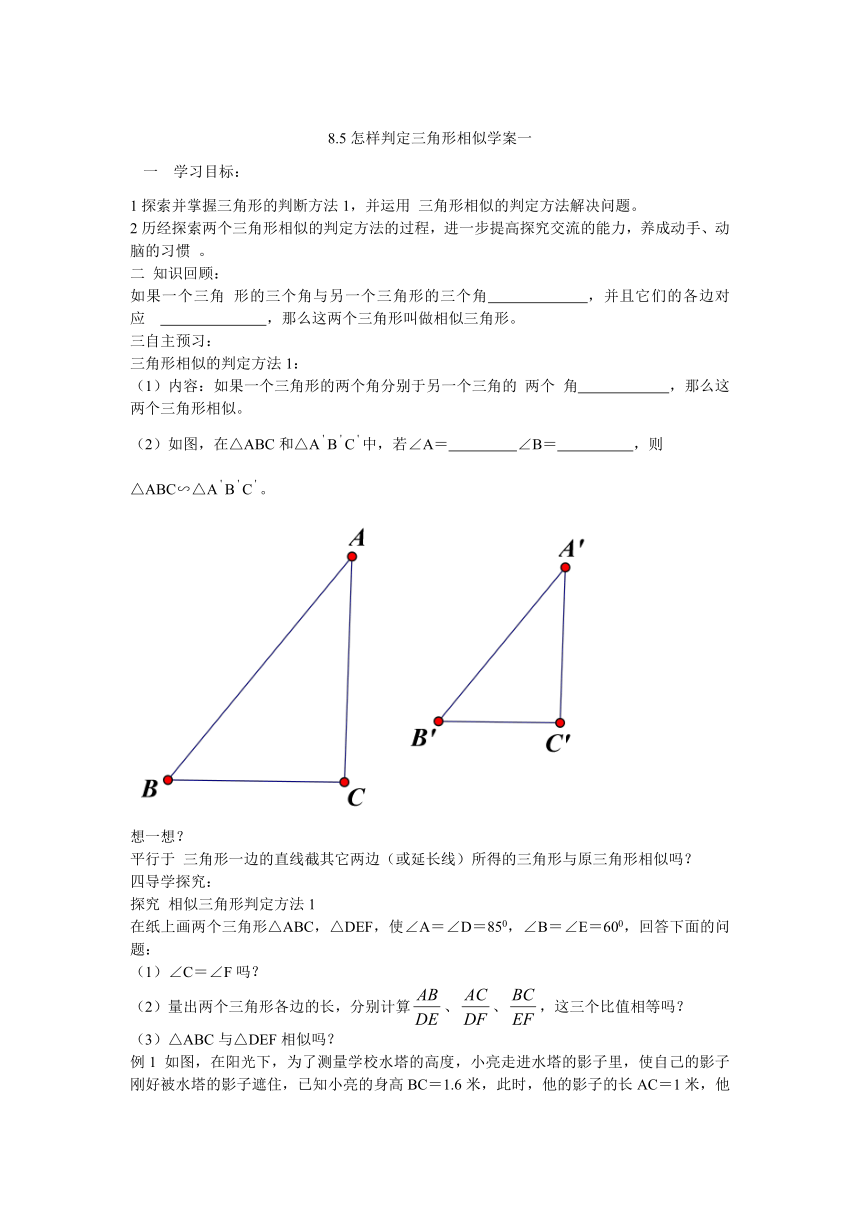
（1）内容：如果一个三角形的两个角分别于另一个三角的 两个 角 ，那么这两个三角形相似。
（2）如图，在△ABC和△ABC中，若∠A＝ ∠B＝ ，则
△ABC∽△ABC。
想一想？
平行于 三角形一边的直线截其它两边（或延长线）所得的三角形与原三角形相似吗？
四导学探究：
探究 相似三角形判定方法1
在纸上画两个三角形△ABC，△DEF，使∠A＝∠D＝850，∠B＝∠E＝600，回答下面的问题：
（1）∠C＝∠F吗？
（2）量出两个三角形各边的长，分别计算、、，这三个比值相等吗？
（3）△ABC与△DEF相似吗？
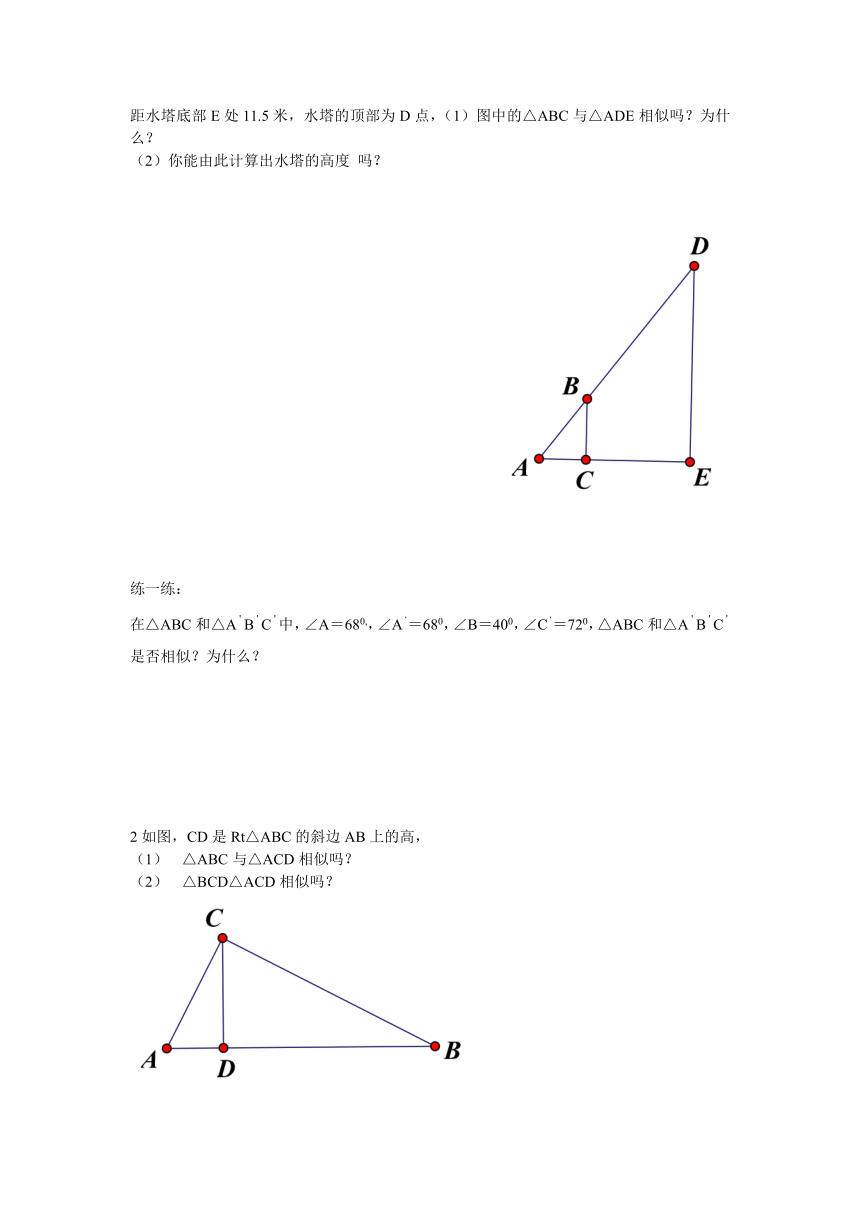
例1 如图，在阳光下，为了测量学校水塔的高度，小亮走进水塔的影子里，使自己的影子刚好被水塔的影子遮住，已知小亮的身高BC＝1.6米，此时，他的影子的长AC＝1米，他距水塔底部E处11.5米，水塔的顶部为D点，（1）图中的△ABC与△ADE相似吗？为什么？
（2）你能由此计算出水塔的高度 吗？
练一练：
在△ABC和△ABC中，∠A＝680,，∠A‘＝680，∠B＝400，∠C‘＝720，△ABC和△ABC是否相似？为什么？
2如图，CD是Rt△ABC的斜边AB上的高，
（1） △ABC与△ACD相似吗？
（2） △BCD△ACD相似吗？
当堂达标
1 如图，AC是矩形ABCD的对角线，E是边BC延长线上一点，AE与CD交于点F,则图中相似三角形共有（ ）
A 2对 B 3对 C 4对 D 5对
2 如图，小东用长为3.2m的竹竿做测量工具测量学校旗杆的高度，移动竹竿，使竹竿、旗杆顶端的影子恰好落在地面的同一点，此时，竹竿与这一点相距8m，与旗杆相距22m，则旗杆的高为（ ）
A 12m B 10m C 8m D 7m
3 小明在一次军事夏令营活动中，进行打靶训练，在用枪瞄准目标点B时，要使眼睛O、准星A、目标B在在同一直线上，如图所示，射击时，小明有轻微的抖动，致使准星A偏离到A/,若OA=0.2米，OB=40米，A A/=0.0015米，则小明射击到的点B/偏离目标点B的长度点B的长度B B/ 为（ ）
A 3米 B 0.3米 C 0.03米 D 0.2米
4 如图，等边△ABC的边长为3，P为BC上一点，且BP=1，D为AC上一点，若∠APD=60度，则CD的长为( )
A °
5 如图，在△ABC中，BD、CE是高，且BD、CE交于点F，则图中与△AEC相似（不包括其本身）的三角形有( ) A 1个 B2个 C3个 D4个
6 如图，在Rt△ABC中，CD是斜边上的高，∠ACD=400，则∠EBC=
7 如图，由已知条件得x＝
8.如图，在梯形ABCD中，AD∥BC,∠B＝∠ACD.若AC＝6，BC＝9.试求AD的长度。
9 如图，△ABC是等边三角形，CE是外角平分线，点D在AC上，连接BD并延长与CE交与点E.
(1)试说明△ABD∽△CED
（2）若AB＝6，AD＝2AD,求BE的长。
8m
22m
B/
A/
1
450
300
2
x
1050
300