一元二次根与系数关系

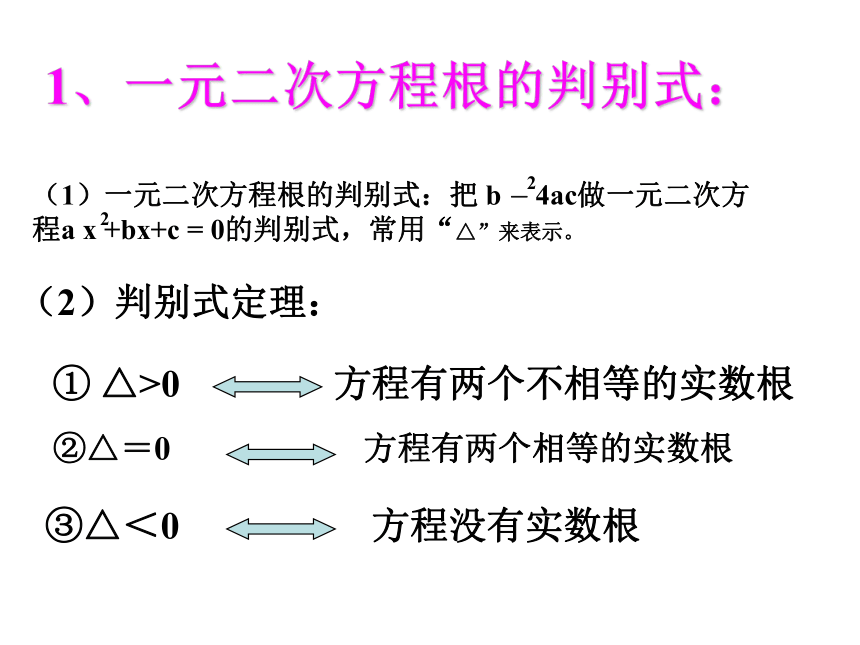
课件12张PPT。一元二次方程根的判别式和根与系数的关系ax2 + bx + c = 01、一元二次方程根的判别式：（1）一元二次方程根的判别式：把 b － 4ac做一元二次方程a x +bx+c = 0的判别式，常用“△”来表示。22（2）判别式定理：①、△﹥0　　　　方程有两个不相等的实数根②△＝0　　　　 方程有两个相等的实数根③△＜0　　　　　方程没有实数根① △>0　　　 方程有两个不相等的实数根（3）实际应用：例1 不解下列方程判别下列方程的根的情况
（1）3x2 -4x+7=0
（2） x2 +x+1=0
（3）2x2 - x-1=0例2（1）m取什么值时，方程 x2+(2m+1)x+ m2-4=0有两个相等的实数解
（2）求证:不论k为何值， 关于x的方程x2＋(２k＋1)x＋k -1 = ０ 总有两个不相等的实数根。（3）实际应用：关于x 的方程m2x2+(2m+1)x+1=0 有两个不相等的
实数根，则m_________________变题1：关于x 的方程m2x2+(2m+1)x+1=0 有两个相等的实数
根，则m___________________变题2：关于x 的方程m2x2+(2m+1)x+1=0 没有实数根，则
m___________________变题3：关于x 的方程m2x2+(2m+1)x+1=0 有两实数根，则
m___________________
且（ b2-4ac=4m+1 ）且2、一元二次方程与系数的关系：（1）、一元二次程的根与系数的关系（韦达定理）：如果ax + bx +c =0(a ≠0)的两个根是 x 、x 那么x + x = －b/a ,x x = c/a 11 22122（2）、根与系数关系定理的推论：推论1：如果方程 x + px +q = 0 的两个根为 x 、 x , 那么x + x = －p , x x = q ,1112222推论2：以两个数 x 、x 为根的一元二次方程（二次项系数为1）是x －(x + x )x + x x = 0 一元二次方程的构造公式12 2 2 2 11例 3、不解方程，求方程两根的和两根的积：①②练 1、不解方程，求方程两根的和两根的积：练2、已知方程 的一个根是2，求它的另一个根及 的值。练3、（1）已知关于x的方程 的两个根是1和2，求p和q的值； （2）求一个一元二次方程，使它的两个根分别为4和-7。例4 1.利用根与系数的关系，求一元二次方程　　　　　　　　　
2x2＋3x－1＝0两根的
(1)平方和；(2)倒数和．2.已知方程 x 2 + ( 2m －2)x + 2m + 1 = 0有两个正根，求m的取值范围练 不解方程，求一元二次方程 两个根的①平方和；②倒数和。练 已知方程的两个根的倒数和等于6，求m的值