16.3.2 分式方程的应用(1)
文档属性
| 名称 | 16.3.2 分式方程的应用(1) |  | |
| 格式 | rar | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-03-15 17:36:00 | ||
图片预览






文档简介
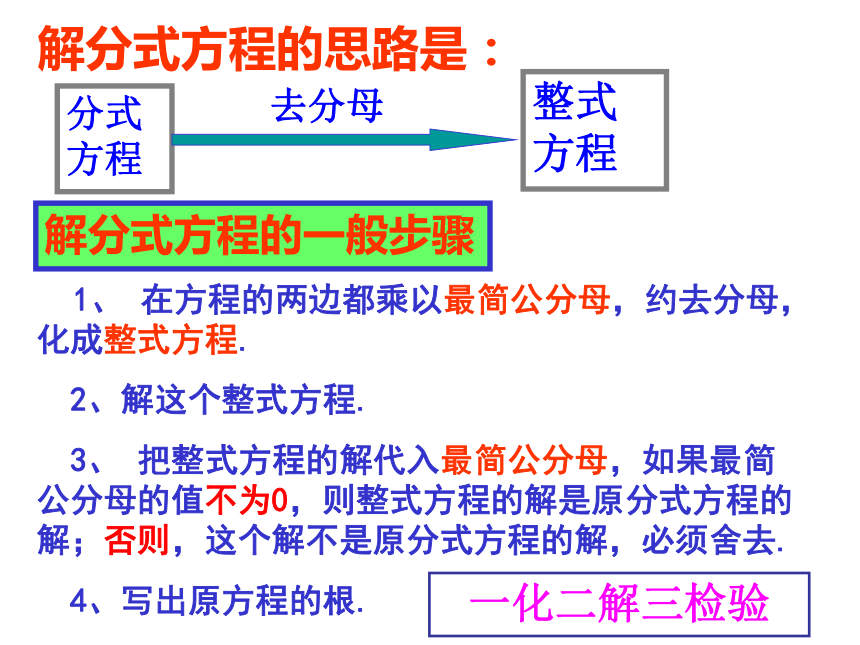
课件23张PPT。南门学校八年(3)(5)班16.3.2 分式方程的应用(1) 解分式方程的一般步骤 1、 在方程的两边都乘以最简公分母,约去分母,化成整式方程.
2、解这个整式方程.
3、 把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解,必须舍去.
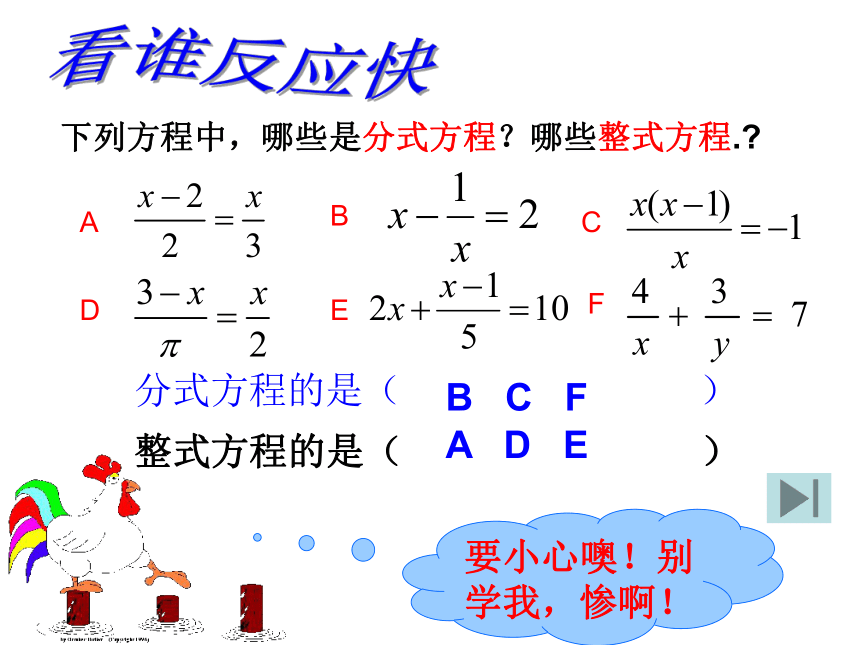
4、写出原方程的根.解分式方程的思路是:分式方程整式方程去分母一化二解三检验看谁反应快下列方程中,哪些是分式方程?哪些整式方程.?A BCDEF要小心噢!别学我,惨啊!分式方程的是( )整式方程的是( )B C FA D E解下列方程 :巩固练习 我能行解:原方程变为去分母,得:解得:x=0检验:x=0时,
x(x-2)=0。
∴原方程无解。解:原方程变为去分母,得:解得:y=3/2检验:x=3/2时,
x(x-2)≠0。
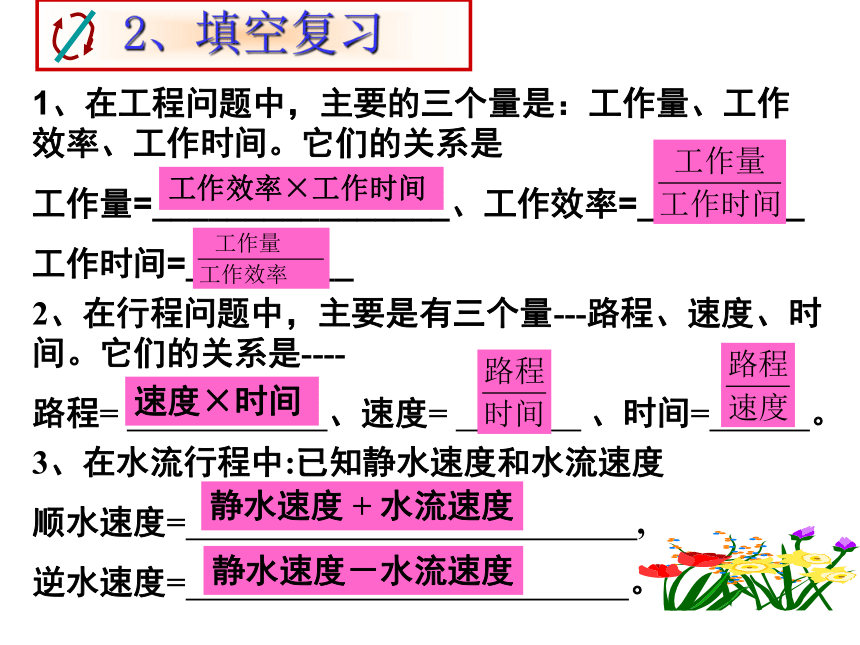
∴x=3/2是原方程的解。解:由题意,得:x=3.去分母,得:k+2(x-3)=4-x ①将x=3代入①,得: k+2(3-3)=4-3解得:k=12、在行程问题中,主要是有三个量---路程、速度、时间。它们的关系是----
路程= 、速度= 、时间= 。 3、在水流行程中:已知静水速度和水流速度
顺水速度= ,
逆水速度= 。速度×时间静水速度 + 水流速度静水速度-水流速度1、在工程问题中,主要的三个量是:工作量、工作效率、工作时间。它们的关系是
工作量=________________、工作效率=_________
工作时间=_________工作效率×工作时间[例1] 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成。哪个队的施工速度快?解:设乙队如果单独施工一个月能完成总工程的 .记总工程量为1,根据题意,得= 1解得经检验知 :x = 1 是原方程的解.由上可知,若乙队单独工作一个月可以完成全部任务,
所以乙队施工速度快.列分式方程解应用题的方法和步骤如下:问题:请分析列分式方程解应用题与以前学习的列方程解应用题有什么区别?1、审题分析题意
2、设未知数
3、根据题意找相等关系,列出方程;
4、解方程,并验根(对解分式方程尤为重要)
5、写答案区别:解方程后要检验。【例4】从2004年5月起某列车平均提速v千米/小时,用相同的时间,列车提速前行驶s千米,提速后比提速前多行驶50千米,提速前列车的平均速度为多少?分析:这里的v、s表示已知数据,设提速前列车的平均速度为x千米/时,先考虑下面的填空: 提速前列车行驶s千米所用的时间为 小时,提速后列车的平均速度为 千米/时,提速后列车运行 千米
所用时间为 小时。根据行驶时间的等量关系可以列出方程(x+V)(s+50) 1.某单位将沿街的一部分房屋出租,每间房屋的租金第二年比第一年多500元,所有房屋的租金第一年为9.6万元,第二年为10.2万元.
(1)分别求两年每间出租房屋的租金?
(2)求出租房屋的总间数?练习解法1:设共有x间出租房.解法2:设第一年每间房屋的租金为x元.2.某市从今年1月1日起调整居民用水价格,每吨水费上涨三分之一,小丽家去年12月的水费是15元,今年2月的水费是30元.已知今年2月的用水量比去年12月的用水量多5吨,求该市今年居民用水的价格?设该市去年用水的价格为x元/吨.3.一艘轮船逆流航行2km的时间比顺流航行2 km的时间多用了40分钟, . (在横线上补充一个条件并提出一个问题) 如:条件:已知水速为2 km/h, 问题:求船在静水中的速度?解:设船在静水中的速度为x km/h.列分式方程解应用题的方法和步骤如下:问题:请分析列分式方程解应用题与以前学习的列方程解应用题有什么区别?1、审题分析题意 2、设未知数
3、根据题意找相等关系,列出方程;
4、解方程,并验根(对解分式方程尤为重要)
5、写答案区别:解方程后要检验。小结补充练习1、一项工程,需要在规定日期内完成,如果甲队独做,恰好如期完成,如果乙队独做,就要超过规定3天,现在由甲、乙两队合作2天,剩下的由乙队独做,也刚好在规定日期内完成,问规定日期是几天?2、购一年期债券,到期后本利只获2700元,如果债券年利率12.5%,那么利息是多少元?3、骑自行车翻越一个坡地,上坡1千米,下坡1千米,如果上坡的速度是25千米/时,那么下坡要保持什么速度才能使全程的平均速度是30千米/时? 4、解一组方程,先用小计算器解20分钟,再改用大计算器解25分钟可解完,如果大计算器的运算速度是小计算器的4倍,并用计算器解这组方程需多少时间? 5、甲、乙两列车分别从相距300千米的A、B两站同时相向而行。相遇后,甲车再经过2小时到达B站,乙车再经过4小时30分到达A站,求甲、乙两车的速度。6、编写一道与下面分式方程相符的实际问题.7..某工人师傅先后两次加工零件各1500个,当第二次加工时,他革新了工具,改进了操作方法,结果比第一次少用了18个小时.已知他第二次加工效率是第一次的2.5倍,求他第二次加工时每小时加工多少零件? 列分式方程解应用题的一般步骤1.审:分析题意,找出数量关系和相等关系.
2.设:选择恰当的未知数,注意单位和语言完整.
3.列:根据数量和相等关系,正确列出方程.
4.解:认真仔细解这个分式方程.
5.验:检验.(是否是分式方程的根, 是否符合题意)
6.答:注意单位和语言完整.【巩固练习,我能行!】4、a=4a=4或6当m为何值时,去分母解方程:
会产生增根?反思:分式方程产生增根,也就是使分母等于0.
将原分式方程去分母后,代入增根.没有解.议一议,启迪思维2、某项工程,甲、乙两队合作,8天可以完成,需要费用3520元,若甲队单独做6天,剩下的工程由乙队单独做,乙队还需12天完成,需要费用3480元,问:
(1)甲、乙两队完成此项工程各需多少天?
(2)甲、乙两队完成此项工程各需费用多少元?
(3)在不考虑工作时间的前提下这项工程由哪支工程队做更合算?解:(2)设甲、乙两队每天的费用分别为a元、b元。2、某项工程,甲、乙两队合作,8天可以完成,需要费用3520元,若甲队单独做6天,剩下的工程由乙队单独做,乙队还需12天完成,需要费用3480元,问:
(1)甲、乙两队完成此项工程各需多少天?
(2)甲、乙两队完成此项工程各需费用多少元?
(3)在不考虑工作时间的前提下这项工程由哪支工程队做更合算?解:(3)甲单独完成工程总费用为:
300×12=3600元乙单独完成工程总费用为:
140×24=3360元∴工程由乙队单独完成更合算。3、某商场销售某种商品,第一个月将此商品的进价加价20%作为销售价,共获利6000元,第二个月商场搞促销活动,将商品的进价加价10%作为销售价,第二个月的销售量比第一个月增加了100件,并且商场第二个月多获利2000元,问此商品进价是多少元?商场第二个月共销售多少件?解:设此商品进价为x元。解得:x=500检验:x=500是分式方程的解。答:商品进价为500元/件,第二个月销售160件。再见
2、解这个整式方程.
3、 把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解,必须舍去.
4、写出原方程的根.解分式方程的思路是:分式方程整式方程去分母一化二解三检验看谁反应快下列方程中,哪些是分式方程?哪些整式方程.?A BCDEF要小心噢!别学我,惨啊!分式方程的是( )整式方程的是( )B C FA D E解下列方程 :巩固练习 我能行解:原方程变为去分母,得:解得:x=0检验:x=0时,
x(x-2)=0。
∴原方程无解。解:原方程变为去分母,得:解得:y=3/2检验:x=3/2时,
x(x-2)≠0。
∴x=3/2是原方程的解。解:由题意,得:x=3.去分母,得:k+2(x-3)=4-x ①将x=3代入①,得: k+2(3-3)=4-3解得:k=12、在行程问题中,主要是有三个量---路程、速度、时间。它们的关系是----
路程= 、速度= 、时间= 。 3、在水流行程中:已知静水速度和水流速度
顺水速度= ,
逆水速度= 。速度×时间静水速度 + 水流速度静水速度-水流速度1、在工程问题中,主要的三个量是:工作量、工作效率、工作时间。它们的关系是
工作量=________________、工作效率=_________
工作时间=_________工作效率×工作时间[例1] 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成。哪个队的施工速度快?解:设乙队如果单独施工一个月能完成总工程的 .记总工程量为1,根据题意,得= 1解得经检验知 :x = 1 是原方程的解.由上可知,若乙队单独工作一个月可以完成全部任务,
所以乙队施工速度快.列分式方程解应用题的方法和步骤如下:问题:请分析列分式方程解应用题与以前学习的列方程解应用题有什么区别?1、审题分析题意
2、设未知数
3、根据题意找相等关系,列出方程;
4、解方程,并验根(对解分式方程尤为重要)
5、写答案区别:解方程后要检验。【例4】从2004年5月起某列车平均提速v千米/小时,用相同的时间,列车提速前行驶s千米,提速后比提速前多行驶50千米,提速前列车的平均速度为多少?分析:这里的v、s表示已知数据,设提速前列车的平均速度为x千米/时,先考虑下面的填空: 提速前列车行驶s千米所用的时间为 小时,提速后列车的平均速度为 千米/时,提速后列车运行 千米
所用时间为 小时。根据行驶时间的等量关系可以列出方程(x+V)(s+50) 1.某单位将沿街的一部分房屋出租,每间房屋的租金第二年比第一年多500元,所有房屋的租金第一年为9.6万元,第二年为10.2万元.
(1)分别求两年每间出租房屋的租金?
(2)求出租房屋的总间数?练习解法1:设共有x间出租房.解法2:设第一年每间房屋的租金为x元.2.某市从今年1月1日起调整居民用水价格,每吨水费上涨三分之一,小丽家去年12月的水费是15元,今年2月的水费是30元.已知今年2月的用水量比去年12月的用水量多5吨,求该市今年居民用水的价格?设该市去年用水的价格为x元/吨.3.一艘轮船逆流航行2km的时间比顺流航行2 km的时间多用了40分钟, . (在横线上补充一个条件并提出一个问题) 如:条件:已知水速为2 km/h, 问题:求船在静水中的速度?解:设船在静水中的速度为x km/h.列分式方程解应用题的方法和步骤如下:问题:请分析列分式方程解应用题与以前学习的列方程解应用题有什么区别?1、审题分析题意 2、设未知数
3、根据题意找相等关系,列出方程;
4、解方程,并验根(对解分式方程尤为重要)
5、写答案区别:解方程后要检验。小结补充练习1、一项工程,需要在规定日期内完成,如果甲队独做,恰好如期完成,如果乙队独做,就要超过规定3天,现在由甲、乙两队合作2天,剩下的由乙队独做,也刚好在规定日期内完成,问规定日期是几天?2、购一年期债券,到期后本利只获2700元,如果债券年利率12.5%,那么利息是多少元?3、骑自行车翻越一个坡地,上坡1千米,下坡1千米,如果上坡的速度是25千米/时,那么下坡要保持什么速度才能使全程的平均速度是30千米/时? 4、解一组方程,先用小计算器解20分钟,再改用大计算器解25分钟可解完,如果大计算器的运算速度是小计算器的4倍,并用计算器解这组方程需多少时间? 5、甲、乙两列车分别从相距300千米的A、B两站同时相向而行。相遇后,甲车再经过2小时到达B站,乙车再经过4小时30分到达A站,求甲、乙两车的速度。6、编写一道与下面分式方程相符的实际问题.7..某工人师傅先后两次加工零件各1500个,当第二次加工时,他革新了工具,改进了操作方法,结果比第一次少用了18个小时.已知他第二次加工效率是第一次的2.5倍,求他第二次加工时每小时加工多少零件? 列分式方程解应用题的一般步骤1.审:分析题意,找出数量关系和相等关系.
2.设:选择恰当的未知数,注意单位和语言完整.
3.列:根据数量和相等关系,正确列出方程.
4.解:认真仔细解这个分式方程.
5.验:检验.(是否是分式方程的根, 是否符合题意)
6.答:注意单位和语言完整.【巩固练习,我能行!】4、a=4a=4或6当m为何值时,去分母解方程:
会产生增根?反思:分式方程产生增根,也就是使分母等于0.
将原分式方程去分母后,代入增根.没有解.议一议,启迪思维2、某项工程,甲、乙两队合作,8天可以完成,需要费用3520元,若甲队单独做6天,剩下的工程由乙队单独做,乙队还需12天完成,需要费用3480元,问:
(1)甲、乙两队完成此项工程各需多少天?
(2)甲、乙两队完成此项工程各需费用多少元?
(3)在不考虑工作时间的前提下这项工程由哪支工程队做更合算?解:(2)设甲、乙两队每天的费用分别为a元、b元。2、某项工程,甲、乙两队合作,8天可以完成,需要费用3520元,若甲队单独做6天,剩下的工程由乙队单独做,乙队还需12天完成,需要费用3480元,问:
(1)甲、乙两队完成此项工程各需多少天?
(2)甲、乙两队完成此项工程各需费用多少元?
(3)在不考虑工作时间的前提下这项工程由哪支工程队做更合算?解:(3)甲单独完成工程总费用为:
300×12=3600元乙单独完成工程总费用为:
140×24=3360元∴工程由乙队单独完成更合算。3、某商场销售某种商品,第一个月将此商品的进价加价20%作为销售价,共获利6000元,第二个月商场搞促销活动,将商品的进价加价10%作为销售价,第二个月的销售量比第一个月增加了100件,并且商场第二个月多获利2000元,问此商品进价是多少元?商场第二个月共销售多少件?解:设此商品进价为x元。解得:x=500检验:x=500是分式方程的解。答:商品进价为500元/件,第二个月销售160件。再见
