2.4.1《抛物线的标准方程》(新人教A版选修2-1)
文档属性
| 名称 | 2.4.1《抛物线的标准方程》(新人教A版选修2-1) |

|
|
| 格式 | rar | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-03-12 00:00:00 | ||
图片预览






文档简介
课件17张PPT。课前延伸解析几何研究的两个基本问题:
(1)由曲线求它的方程
(2)利用方程研究它的性质
求曲线方程的步骤:
(1)建系(2)设点(3)列式(4)化简
两点间的距离公式
点到直线的距离公式
?动一动手生活中存在着各种形式的抛物线2.4.1抛物线的标准方程青云学府高二数学组 王斌抛物线的标准方程学习重点:
1、抛物线的定义;
2、根据具体条件求抛物线的标准方程;
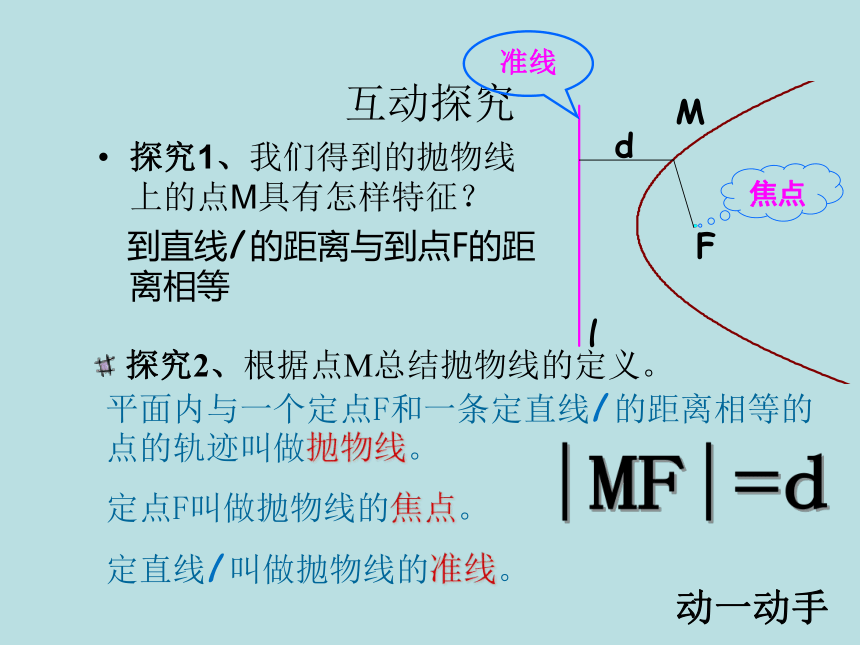
3、由标准方程求焦点坐标、准线方程。互动探究探究1、我们得到的抛物线上的点M具有怎样特征?
到直线l 的距离与到点F的距离相等MFl准线焦点d探究2、根据点M总结抛物线的定义。平面内与一个定点F和一条定直线l 的距离相等的点的轨迹叫做抛物线。
定点F叫做抛物线的焦点。
定直线l 叫做抛物线的准线。动一动手互动探究?MFl准线焦点d若定点F在定直线l上,那么动点的轨迹是什么图形?过点F且垂直于l的直线?方程推导如何建立直角坐标系?想一想K设|FK|=p(p>0)方程推导KKK化简后得:
y2 = 2px (p>0)化简后得:
y2 = 2px + p2 (p>0)化简后得:
y2 = 2px - p2 (p>0) d|MF|=d设|FK|=p抛物线的标准方程方程 y2 = 2px(p>0)叫做抛物线的标准方程。
它表示的抛物线的焦点在x轴的正半轴上
焦点:
准线:
顶点:
开口方向:
思考:常数p的几何意义是什么?
焦 点 到 准 线 的 距 离??(0,0)开口向右典例讲解例1:已知抛物线的标准方程是y2=6x,求它的焦点坐标和准线方程.
解:因为p=3,所以抛物线的焦点坐标是 , 准线方程是x= ;?典型例题??典型例题例3:点M与点F(4,0)的距离比它到直线 : 的距离小1,求点M的轨迹方程。
解:由题意可知,M到x=-4距离比到x=-5距离小1,
所以M到x=-4和到(4,0)距离相等,
所以M的轨迹是以F(4,0)为焦点,直线x=-4为准线的抛物线,
其轨迹方程为y2=16x典型例题例4:
抛物线y2 = 12x上到焦点的距离等于9的点的坐标是 。?归纳总结 收获了
什么?
抛物线 两端长 漫漫长路向远方
似彩虹 如桥梁 世间英雄竞畅想
嫦娥飞 人气涨 主宰神灵非天王
看今朝 我辈忙 书山崎岖心飘香再见
(1)由曲线求它的方程
(2)利用方程研究它的性质
求曲线方程的步骤:
(1)建系(2)设点(3)列式(4)化简
两点间的距离公式
点到直线的距离公式
?动一动手生活中存在着各种形式的抛物线2.4.1抛物线的标准方程青云学府高二数学组 王斌抛物线的标准方程学习重点:
1、抛物线的定义;
2、根据具体条件求抛物线的标准方程;
3、由标准方程求焦点坐标、准线方程。互动探究探究1、我们得到的抛物线上的点M具有怎样特征?
到直线l 的距离与到点F的距离相等MFl准线焦点d探究2、根据点M总结抛物线的定义。平面内与一个定点F和一条定直线l 的距离相等的点的轨迹叫做抛物线。
定点F叫做抛物线的焦点。
定直线l 叫做抛物线的准线。动一动手互动探究?MFl准线焦点d若定点F在定直线l上,那么动点的轨迹是什么图形?过点F且垂直于l的直线?方程推导如何建立直角坐标系?想一想K设|FK|=p(p>0)方程推导KKK化简后得:
y2 = 2px (p>0)化简后得:
y2 = 2px + p2 (p>0)化简后得:
y2 = 2px - p2 (p>0) d|MF|=d设|FK|=p抛物线的标准方程方程 y2 = 2px(p>0)叫做抛物线的标准方程。
它表示的抛物线的焦点在x轴的正半轴上
焦点:
准线:
顶点:
开口方向:
思考:常数p的几何意义是什么?
焦 点 到 准 线 的 距 离??(0,0)开口向右典例讲解例1:已知抛物线的标准方程是y2=6x,求它的焦点坐标和准线方程.
解:因为p=3,所以抛物线的焦点坐标是 , 准线方程是x= ;?典型例题??典型例题例3:点M与点F(4,0)的距离比它到直线 : 的距离小1,求点M的轨迹方程。
解:由题意可知,M到x=-4距离比到x=-5距离小1,
所以M到x=-4和到(4,0)距离相等,
所以M的轨迹是以F(4,0)为焦点,直线x=-4为准线的抛物线,
其轨迹方程为y2=16x典型例题例4:
抛物线y2 = 12x上到焦点的距离等于9的点的坐标是 。?归纳总结 收获了
什么?
抛物线 两端长 漫漫长路向远方
似彩虹 如桥梁 世间英雄竞畅想
嫦娥飞 人气涨 主宰神灵非天王
看今朝 我辈忙 书山崎岖心飘香再见
