《特殊的平行四边形》复习

课件13张PPT。《特殊的平行四边形》
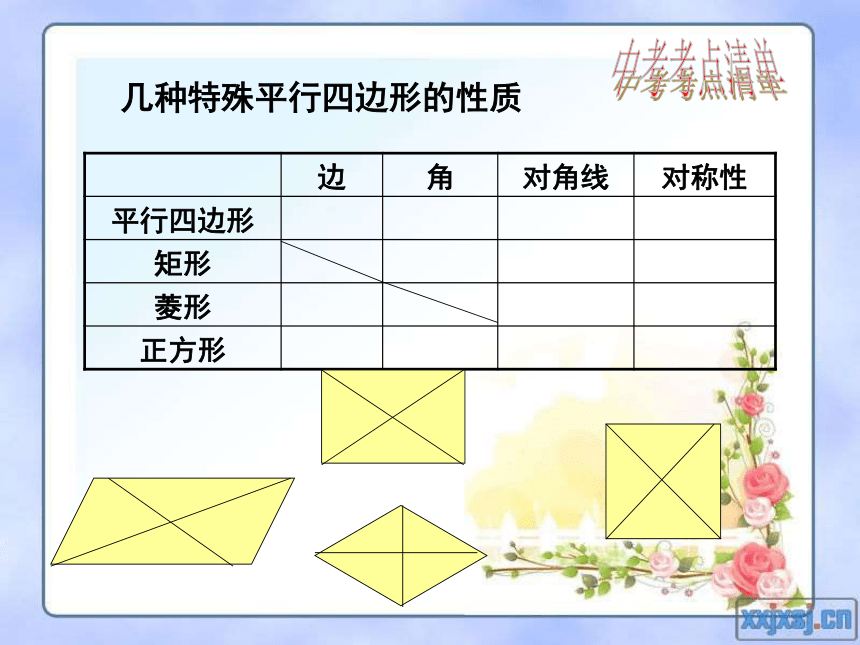
复 习学习目标1、理解矩形、菱形、正方形与平行四边形的关系。
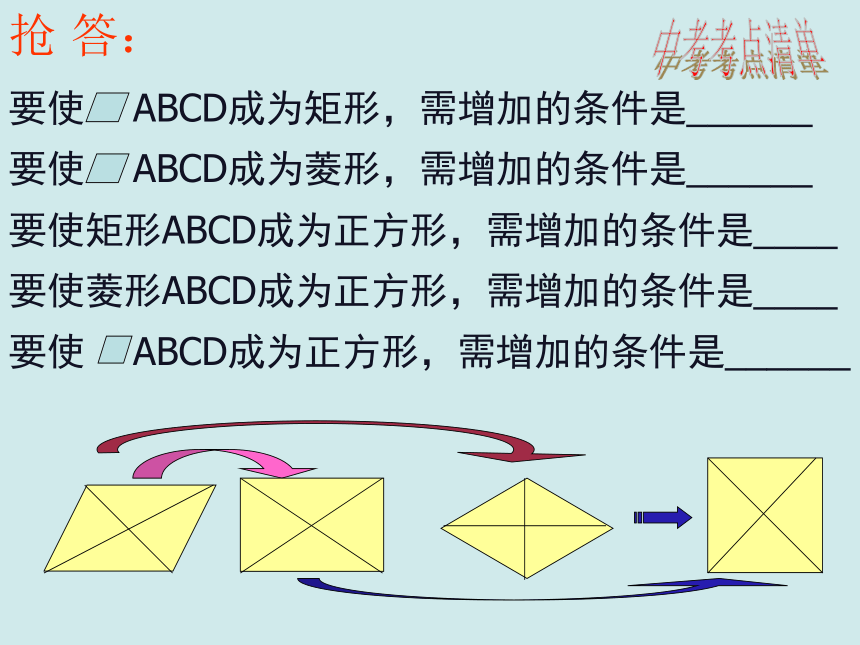
2、掌握特殊平行四边形的有关性质及判定方法，并能应用所学知识解决相关问题。几种特殊平行四边形的性质中考考点清单要使矩形ABCD成为正方形，需增加的条件是____ 要使菱形ABCD成为正方形，需增加的条件是____要使 ABCD成为正方形，需增加的条件是______抢 答：中考考点清单1、(2010义乌)下列说法不正确的是_______
A、一组邻边相等的平行四边形是菱形。
B、两条对角线互相平分的四边形是平行四边形。
C、一组邻边相等且一个角为直角的四边形是正方形。
D、对角线平分一个内角的矩形是正方形。
2、（2010北京）若菱形两条对角线的长分别为6cm和8cm，这个菱形的周长为_______cm，面积为__________cm2。
3、（2010济南）如图所示，正方形ABCD中，对角线AC、BD交于点O，
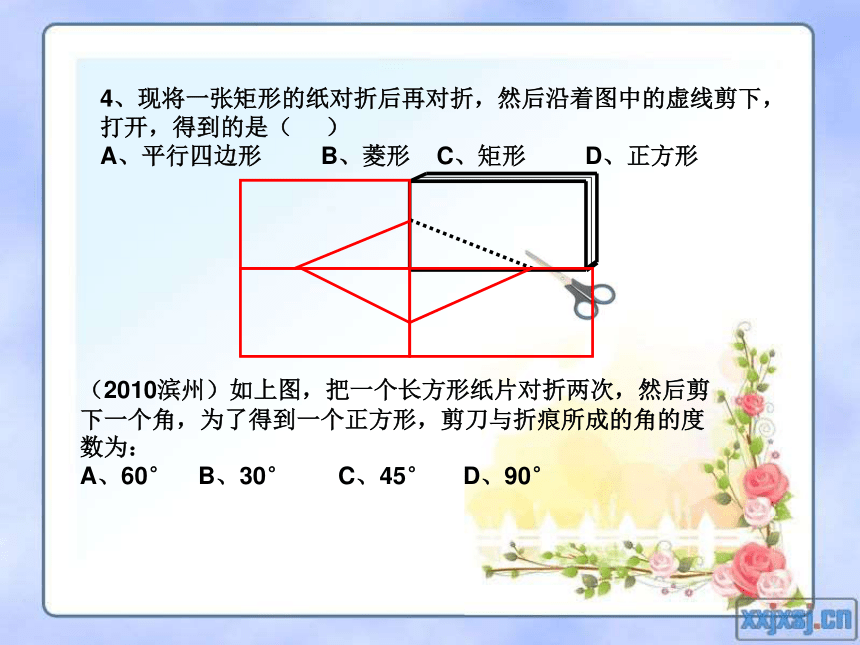
点Ｍ、Ｎ分别为OB、OC的中点，则cos∠OMN的值为：考点再现C2024B4、现将一张矩形的纸对折后再对折，然后沿着图中的虚线剪下，打开，得到的是（ ）
A、平行四边形 B、菱形 C、矩形 D、正方形（2010滨州）如上图，把一个长方形纸片对折两次，然后剪下一个角，为了得到一个正方形，剪刀与折痕所成的角的度数为：
A、60° B、30°　　C、45° D、90°6、（2009济宁）“赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形。如图，是一“赵爽弦图”飞镖板，其直角三角形的两条直角边的长分别是2和4，小明同学距飞镖板一定距离向飞镖板投掷飞镖（假设投掷的飞镖均扎在飞镖板上），则投掷一次飞镖扎在中间小正方形区域（含边线）的概率是：
A、0.5 B、0.25 C、0.2 D、0.15、（2010上海市）如图，正方形ABCD中，E为CD上一点，DE=2，EC=1。将线段AE以A点为中心旋转，使点E落在直线BC上的F点，则点F、C的距离等于______________。FF1或4C例：如图，矩形ABCD的对角线AC、BD交于点O，过点D作DP∥OC，且 DP=OC，连结CP，试判断四边形CODP的形状．结论：四边形CODP是菱形 典例解析证明： ∵ DP∥OC， DP=OC，
∴ 四边形CODP是平行四边形．
∵四边形ABCD是矩形 ，
　 ∴CO=DO．
∴四边形CODP是菱形 ．
如果题目中的矩形变为正方形，结论又会变为什么？如果题目中的矩形变为菱形，结论会变为什么？ 例：如图，矩形ABCD的对角线AC、BD交于点O，过点D作DP∥OC，且 DP=OC，连结CP，试判断四边形CODP的形状．⒈矩形、菱形、正方形都具有的性质是（ ）
A、对角线相等 B、对角线互相平分
C、对角线互相垂直 D、四条边都相等
⒉已知矩形的一条对角线与一边的夹角是40°，则两条对角线所成的锐角的度数（ ）
A、50° B、60° C、70° D、80°
3、菱形的周长为32cm，若有一个内角为120°，
则菱形的一条较短的对角线为_____cm.
聚焦中考BD84、（2010丹东）如图，已知矩形ABCＤ中，Ｅ为ＡD上的一个点，F是AB上的一个点，EF⊥EC有，且EF=EC，DE=4cm,矩形ABCD的周长为32cm,则AE的长为____________。
5、如图，菱形ABCD的对角线的长分别为2和5，P是对角线AC上任一点（点P不与点A、C重合）且PE∥BC交AB于E，PF∥CD交AD于F，则阴影部分的面积是 ．6cm2.56、（2010绍兴）（1）如图①，在正方形ABCD中，点E、F分别在边BC、CD上，AE、BF交于点O，∠AOF=90°。
求证：AE=BF。
（2）如图②，在正方形ABCD中，点E、H、F、G分别在边AB、BC、CD、DA上，EF、GH交于点O，∠FOH=90°，EF=4，求GH的长。
（3）已知点E、 H、F、G分别在边AB、BC、CD、DA上，EF、GH交于点O，∠FOH=90°，EF=4，直接写出下列两题的答案。
①如图③，矩形ABCD由两个全等的正方形组成，则GH=_________。
②如图④，矩形ABCD由n个全等的正方形组成，则GH=_________（结果用含n的代数式表示）。
MNM再 见！