第二十八章 锐角三角函数精品讲解资料+同步习题
文档属性
| 名称 | 第二十八章 锐角三角函数精品讲解资料+同步习题 |

|
|
| 格式 | rar | ||
| 文件大小 | 853.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-03-15 00:00:00 | ||
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
锐角三角函数精品资料+同步
教学过程:
一、基础知识点:
1.定义:
如图在△ABC中,∠C为直角,
我们把锐角∠A的对边与斜边的比叫做∠A的正弦,记作sinA;
把锐角∠A的邻边与斜边的比叫做∠A的余弦,记作cosA;
把锐角∠A的对边与邻边的比叫做∠A的正切,记作tanA 。
2、三角函数值
(1)特殊角的三角函数值
角度三角函数 0° 30° 45° 60° 90°
sinA 0 1
cosA 1 0
tanA 0 1 不存在
3、 同角、互余角的三角函数关系:
(1)、同角三角函数关系:.; ;
(2)、互余锐角的三角函数关系:,。
1、 解直角三角形:
由直角三角形中除直角以外的两个已知元素(其中至少有一条边),求出所有未知元素的过程,叫做解直角三角形。直角三角形的可解条件及解直角三角形的基本类型如下表:
已知条件 解法
一条边和一个锐角 斜边c和锐角A B=90°-A,a=csinA,b=ccosA,s=c2sinAcosA
直角边a和锐角A B=90°-A,b=acotA,,
两条边 两条直角边a和b ,由,求角A,B=90°-A,S=ab
直角边a和斜边c ,由,求 角A,B=90°-A,S=a
备注:a、b、c为三角形的三边;A、B、C为三角形的三个内角、S为三角形的面积
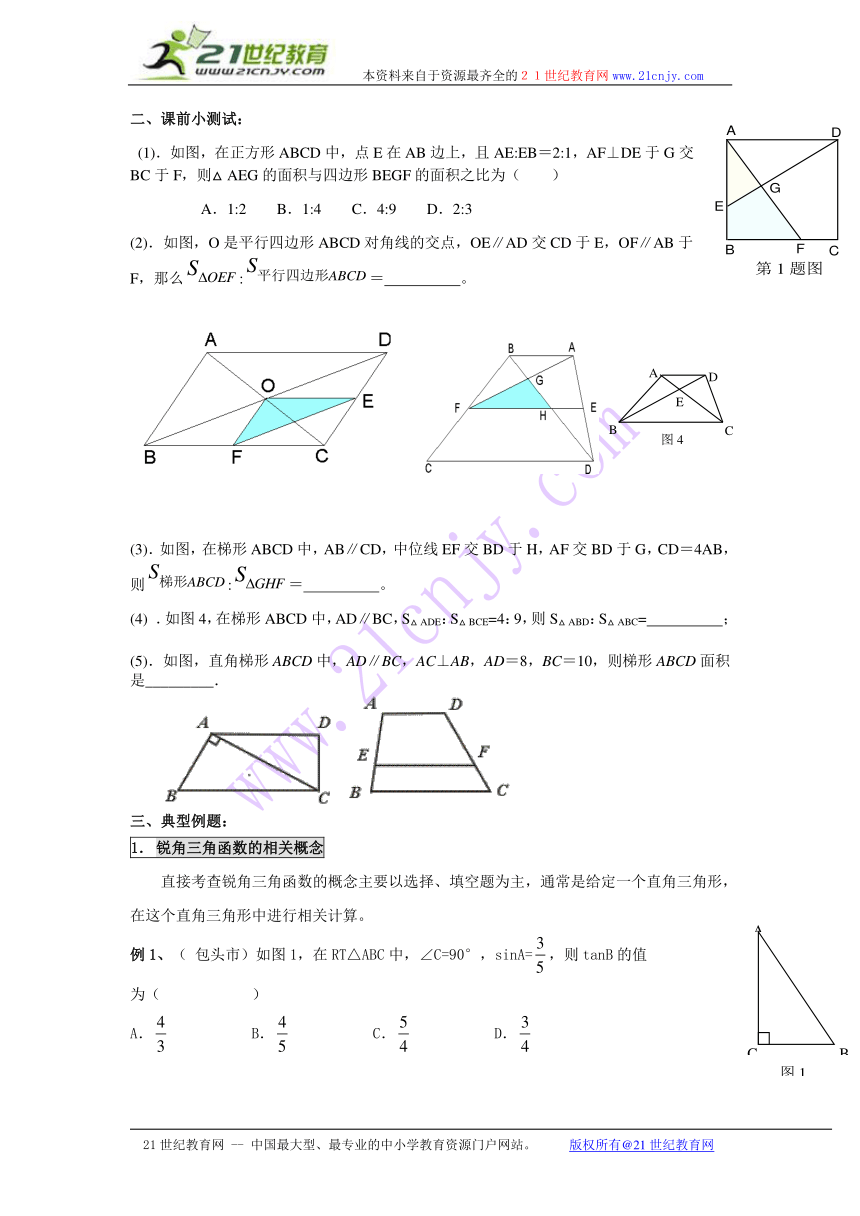
二、课前小测试:
(1).如图,在正方形ABCD中,点E在AB边上,且AE:EB=2:1,AF⊥DE于G交BC于F,则△AEG的面积与四边形BEGF的面积之比为( )
A.1:2 B.1:4 C.4:9 D.2:3
(2).如图,O是平行四边形ABCD对角线的交点,OE∥AD交CD于E,OF∥AB于F,那么:= 。
(3).如图,在梯形ABCD中,AB∥CD,中位线EF交BD于H,AF交BD于G,CD=4AB,则:= 。
(4) .如图4,在梯形ABCD中,AD∥BC,S△ADE:S△BCE=4:9,则S△ABD:S△ABC= ;
(5).如图,直角梯形ABCD中,AD∥BC,AC⊥AB,AD=8,BC=10,则梯形ABCD面积是_________.
三、典型例题:
1. 锐角三角函数的相关概念
直接考查锐角三角函数的概念主要以选择、填空题为主,通常是给定一个直角三角形,在这个直角三角形中进行相关计算。
例1、( 包头市)如图1,在RT△ABC中,∠C=90°,sinA=,则tanB的值
为( )
A. B. C. D.
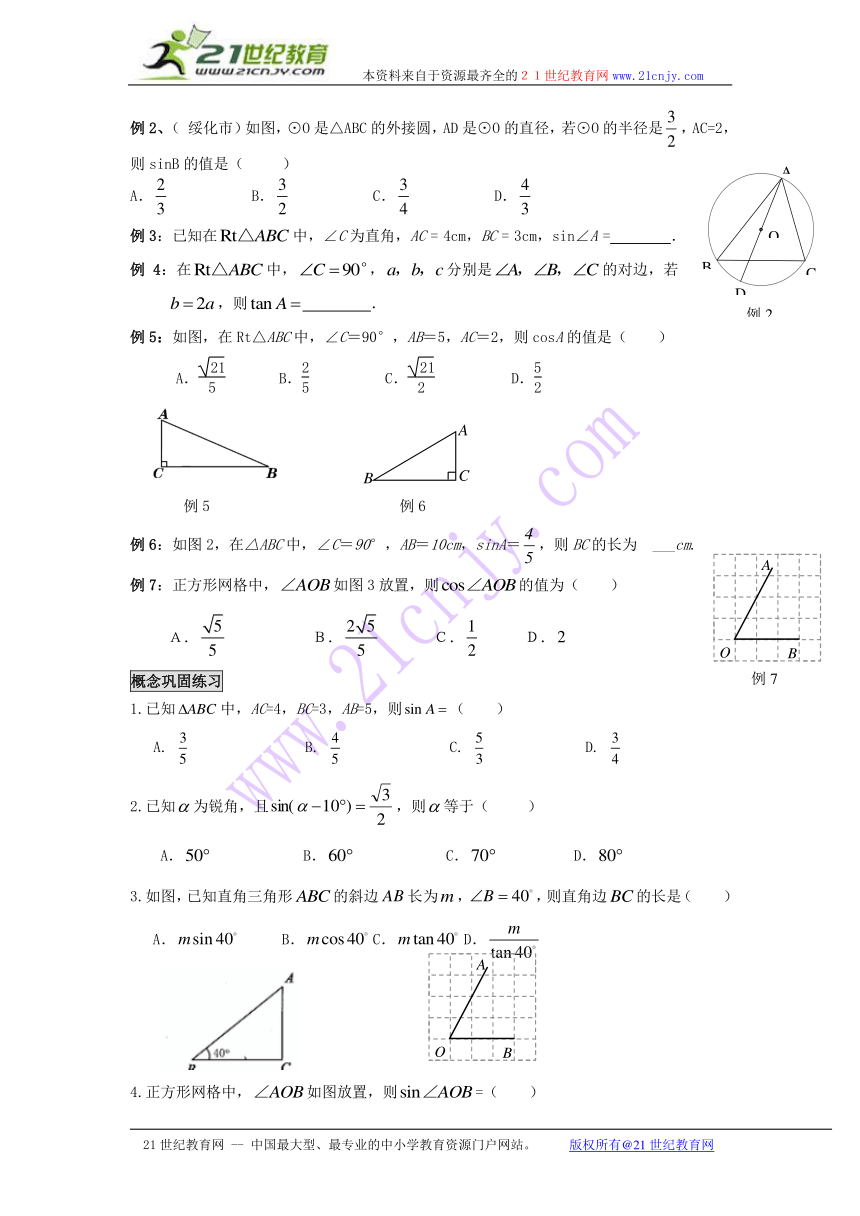
例2、( 绥化市)如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径是,AC=2,则sinB的值是( )
A. B. C. D.
例3:已知在中,∠C为直角,AC = 4cm,BC = 3cm,sin∠A = .
例4:在中,,分别是的对边,若,则 .
例5:如图,在Rt△ABC中,∠C=90°,AB=5,AC=2,则cosA的值是( )
A. B. C. D.
例5 例6
例6:如图2,在△ABC中,∠C=90°,AB=10cm,sinA=,则BC的长为 ___cm.
例7:正方形网格中,如图3放置,则的值为( )
A. B. C. D.
概念巩固练习
1.已知中,AC=4,BC=3,AB=5,则( )
A. B. C. D.
2.已知为锐角,且,则等于( )
A. B. C. D.
3.如图,已知直角三角形的斜边长为,,则直角边的长是( )
A. B. C. D.
4.正方形网格中,如图放置,则=( )
A. B. C. D.
5.在△ABC中,∠C=90°,tanA=,则sinB=( )
A. B. C. D.
6.直角三角形纸片的两直角边长分别为6,8,现将如图那样折叠,使点与点重合,折痕为,则的值是( )
A. B. C. D.
7.如图,在高楼前点测得楼顶的仰角为,向高楼前进60米到点,
又测得仰角为,则该高楼的高度大约为( )
A.82米 B.163米 C.52米 D.70米
2、锐角三角函数的应用性问题
(1)求高
例1、某村计划开挖一条长1500m的水渠,渠道的断面为等腰梯形,上底宽2.8m,下底宽1.2m,坡角为45°,如图1,实际开挖渠道时,每天比原计划多挖土20m3,结果比原计划提前4天完工,求原计划每天挖土多少立方米?
(2)测量问题
例2、某学校宏志班的同学们五一期间去双塔寺观赏牡丹,同时对文宣塔的高度进行了测量,如图2,他们先在A处测得塔顶C的仰角为30°;再向塔的方向直行80步到达B处,又测得塔顶C的仰角为60°,请用以上数据计算塔高。(学生的身高忽略不计,1步=0.8m,结果精确到1m)
(3)、航海问题
例3、如图3,灯塔A在港口0的北偏东55°的方向,且与港口的距离为80海里,一艘船上午9时从港口0出发向正东方向航行,上午11时到达B处,看到灯塔A在它的正北方向,试求这艘船航行的速度(精确到0.01海里/小时)(供选数据:sin55°=0.8192,cos55°=0.5736,tan55°=1.4281)
四、巩固练习:
1. (2009湖州)如图,在中,,,,则下列结论正确的是( )
A. B. C. D.
2. (2009益阳)如图3,先锋村准备在坡角为的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为( )
A. B. C. D.
3. (2009宁波)如图,在坡屋顶的设计图中,AB=AC,屋顶的宽度l为10米,坡角α这35°,则坡屋顶的高度h为 米.(结果精确到0.1米)
4. (2009温州)如图,△ABC中,∠C=90°,AB=8,cosA=,则AC的长是 ;
5. 2009泸州)如图10,已知Rt△ABC中,AC=3,BC= 4,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC,垂足为C1,过C1作C1A2⊥AB,垂足为A2,再过A2作A2C2⊥BC,垂足为C2,…,
这样一直做下去,得到了一组线段CA1,A1C1,,…,则CA1= ,
6. (2009衡阳)某人沿着有一定坡度的坡面前进了10米,此时他与水平地面的垂直距离为米,则这个破面的坡度为
7. (2009仙桃)如图所示,小华同学在距离某建筑物6米的点A处测得广告牌B点、C点的仰角分别为52°和35°,则广告牌的高度BC为_____________米(精确到0.1米).(sin35°≈0.57,cos35°≈0.82,tan35°≈0.70;sin52°≈0.79,cos52°≈0.62,tan52°≈1.28)
8. (2009荆门)=______.
9. (2009义乌)(1) 计算=
10. (2009湖州)(1)计算:=
五、课后练习
1.(2010辽宁丹东市)如图,小颖利用有一个锐角是30°的三角板测量一棵树
的高度,已知她与树之间的水平距离BE为5m,AB为1.5m
(即小颖的眼睛距地面的距离),那么这棵树高是( )
A.()m B.()m C. m D.4m
2.(2010山东日照)如图,在等腰Rt△ABC中,∠C=90o,AC=6,D是AC上一点,若tan∠DBA=,则AD的长为
(A) 2 (B) (C) (D)1
3.(2010四川凉山)已知在中,,设,当是最小的内角时,的取值范围是
A. B. C. D.
4.(2010四川眉山)如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为( )
A.90° B.60° C.45° D.30°
5.(2010 浙江省温州)如图,已知一商场自动扶梯的长z为10米,该自动扶梯到达的高度h为6米,自动扶梯与地面所成的角为θ,则tanθ的值等于( )
6.(2010 浙江台州市)如图,矩形ABCD中,AB>AD,AB=a,AN平分∠DAB,DM⊥AN于点M,CN⊥AN于点N.则DM+CN的值为(用含a的代数式表示)( )
A.a B. C. D.
7.(2010 黄冈)在△ABC中,∠C=90°,sinA=,则tanB=( )
A. B. C. D.
8.(2010年贵州毕节)在正方形网格中,的位置如图所示,则的值为( )
A. B. C. D.
9.(2010湖北荆门)计算sin45°的结果等于( )
A. B.1 C. D.
10.(2010湖南常德)在Rt△ABC中,∠C=90°,若AC=2BC,则sin A的值是( )
A. B.2 C. D.
11.(2010江苏常州)在Rt△ABC中,∠C=90°,AC=2,BC=1,则tanB= ,sinA= 。
12.(2010山东潍坊)直角梯形ABCD中,AB⊥BC,AD∥BC,BC>AD,AD=2,AB=4,点E在AB上,将△CBE沿CE翻折,使得B点与D点重合,则∠BCE的正切值为 .
21世纪教育网 ( http: / / www.21cnjy.com / )
13.(2010广东中山)如图,已知RtΔABC中,斜边BC上的高AD=4,cosB=,则AC= .
14.(2010湖南怀化)在Rt△ABC中,∠C=90°,sinA=,则∠A= .
15.(2010湖北荆州)如图,在△ABC中,∠B=45°,cos∠C=,AC=5a,则△ABC的面积用含a的式子表示是 .
16.如图,某边防巡逻队在一个海滨浴场岸边的A点处发现海中的B点有人求救,便立即派三名救生员前去营救.1号救生员从A点直接跳入海中;2号救生员沿岸边(岸边看成是直线)向前跑到C点,再跳入海中;3号救生员沿岸边向前跑3 0 O米到离B点最近的D点,再跳人海中.救生员在岸上跑的速度都是6米/秒,在水中游泳的速度都是2米/秒.若∠BAD=4 5°,∠BCD=6 0°,三名救生员同时从A点出发,请说明谁先到达营救地点B. (参考数据≈1.4,≈1.7)
17.如图13,某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离是1.7m,看旗杆顶部的仰角为;小红的眼睛与地面的距离是1.5m,看旗杆顶部的仰角为.两人相距28米且位于旗杆两侧(点在同一条直线上).请求出旗杆的高度.(参考数据:,,结果保留整数)
18.小刚有一块含有30°角的直角三角板,他想测量其短直角边的长度,而手中另外只有一个量角器,于是他采用了如下的办法,并获得了相关数据:
第一步,他先用三角板标有刻度的一边测出量角器的直径AB的长度为9cm;
第二步,将三角板与量角器按如图所示的方式摆放,并量得∠BOC为80°(O为AB中点).
请你根据小刚测得的数据,求出三角板的短直角边AC的长.
(参考数据:sin80°=0.98,cos80°=0.17,tan80°=5.67;sin40°=0.64,cos40°=0.77,tan40°=0.84,结果精确到0.1cm.)
A
B
C
D
E
图4
A
C
B
图1
A
B
C
D
O
例2
A
C
B
A
B
O
例7
A
B
O
6
8
C
E
A
B
D
(第6题)
(第7题)
A
B
C
D
E
)
45°
图1
C
D
B
A
图2
A
B
O
北
东
西
南
图3
)
55°
B
C
A
(第1题)
图10
图9
A
B
C
D
6米
52°
35°
(第14题图)
B
A
E
D
C
30°
(第6题)
M
N
BO
A
DO
C
30°
45°
A
B
C
O
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
锐角三角函数精品资料+同步
教学过程:
一、基础知识点:
1.定义:
如图在△ABC中,∠C为直角,
我们把锐角∠A的对边与斜边的比叫做∠A的正弦,记作sinA;
把锐角∠A的邻边与斜边的比叫做∠A的余弦,记作cosA;
把锐角∠A的对边与邻边的比叫做∠A的正切,记作tanA 。
2、三角函数值
(1)特殊角的三角函数值
角度三角函数 0° 30° 45° 60° 90°
sinA 0 1
cosA 1 0
tanA 0 1 不存在
3、 同角、互余角的三角函数关系:
(1)、同角三角函数关系:.; ;
(2)、互余锐角的三角函数关系:,。
1、 解直角三角形:
由直角三角形中除直角以外的两个已知元素(其中至少有一条边),求出所有未知元素的过程,叫做解直角三角形。直角三角形的可解条件及解直角三角形的基本类型如下表:
已知条件 解法
一条边和一个锐角 斜边c和锐角A B=90°-A,a=csinA,b=ccosA,s=c2sinAcosA
直角边a和锐角A B=90°-A,b=acotA,,
两条边 两条直角边a和b ,由,求角A,B=90°-A,S=ab
直角边a和斜边c ,由,求 角A,B=90°-A,S=a
备注:a、b、c为三角形的三边;A、B、C为三角形的三个内角、S为三角形的面积
二、课前小测试:
(1).如图,在正方形ABCD中,点E在AB边上,且AE:EB=2:1,AF⊥DE于G交BC于F,则△AEG的面积与四边形BEGF的面积之比为( )
A.1:2 B.1:4 C.4:9 D.2:3
(2).如图,O是平行四边形ABCD对角线的交点,OE∥AD交CD于E,OF∥AB于F,那么:= 。
(3).如图,在梯形ABCD中,AB∥CD,中位线EF交BD于H,AF交BD于G,CD=4AB,则:= 。
(4) .如图4,在梯形ABCD中,AD∥BC,S△ADE:S△BCE=4:9,则S△ABD:S△ABC= ;
(5).如图,直角梯形ABCD中,AD∥BC,AC⊥AB,AD=8,BC=10,则梯形ABCD面积是_________.
三、典型例题:
1. 锐角三角函数的相关概念
直接考查锐角三角函数的概念主要以选择、填空题为主,通常是给定一个直角三角形,在这个直角三角形中进行相关计算。
例1、( 包头市)如图1,在RT△ABC中,∠C=90°,sinA=,则tanB的值
为( )
A. B. C. D.
例2、( 绥化市)如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径是,AC=2,则sinB的值是( )
A. B. C. D.
例3:已知在中,∠C为直角,AC = 4cm,BC = 3cm,sin∠A = .
例4:在中,,分别是的对边,若,则 .
例5:如图,在Rt△ABC中,∠C=90°,AB=5,AC=2,则cosA的值是( )
A. B. C. D.
例5 例6
例6:如图2,在△ABC中,∠C=90°,AB=10cm,sinA=,则BC的长为 ___cm.
例7:正方形网格中,如图3放置,则的值为( )
A. B. C. D.
概念巩固练习
1.已知中,AC=4,BC=3,AB=5,则( )
A. B. C. D.
2.已知为锐角,且,则等于( )
A. B. C. D.
3.如图,已知直角三角形的斜边长为,,则直角边的长是( )
A. B. C. D.
4.正方形网格中,如图放置,则=( )
A. B. C. D.
5.在△ABC中,∠C=90°,tanA=,则sinB=( )
A. B. C. D.
6.直角三角形纸片的两直角边长分别为6,8,现将如图那样折叠,使点与点重合,折痕为,则的值是( )
A. B. C. D.
7.如图,在高楼前点测得楼顶的仰角为,向高楼前进60米到点,
又测得仰角为,则该高楼的高度大约为( )
A.82米 B.163米 C.52米 D.70米
2、锐角三角函数的应用性问题
(1)求高
例1、某村计划开挖一条长1500m的水渠,渠道的断面为等腰梯形,上底宽2.8m,下底宽1.2m,坡角为45°,如图1,实际开挖渠道时,每天比原计划多挖土20m3,结果比原计划提前4天完工,求原计划每天挖土多少立方米?
(2)测量问题
例2、某学校宏志班的同学们五一期间去双塔寺观赏牡丹,同时对文宣塔的高度进行了测量,如图2,他们先在A处测得塔顶C的仰角为30°;再向塔的方向直行80步到达B处,又测得塔顶C的仰角为60°,请用以上数据计算塔高。(学生的身高忽略不计,1步=0.8m,结果精确到1m)
(3)、航海问题
例3、如图3,灯塔A在港口0的北偏东55°的方向,且与港口的距离为80海里,一艘船上午9时从港口0出发向正东方向航行,上午11时到达B处,看到灯塔A在它的正北方向,试求这艘船航行的速度(精确到0.01海里/小时)(供选数据:sin55°=0.8192,cos55°=0.5736,tan55°=1.4281)
四、巩固练习:
1. (2009湖州)如图,在中,,,,则下列结论正确的是( )
A. B. C. D.
2. (2009益阳)如图3,先锋村准备在坡角为的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为( )
A. B. C. D.
3. (2009宁波)如图,在坡屋顶的设计图中,AB=AC,屋顶的宽度l为10米,坡角α这35°,则坡屋顶的高度h为 米.(结果精确到0.1米)
4. (2009温州)如图,△ABC中,∠C=90°,AB=8,cosA=,则AC的长是 ;
5. 2009泸州)如图10,已知Rt△ABC中,AC=3,BC= 4,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC,垂足为C1,过C1作C1A2⊥AB,垂足为A2,再过A2作A2C2⊥BC,垂足为C2,…,
这样一直做下去,得到了一组线段CA1,A1C1,,…,则CA1= ,
6. (2009衡阳)某人沿着有一定坡度的坡面前进了10米,此时他与水平地面的垂直距离为米,则这个破面的坡度为
7. (2009仙桃)如图所示,小华同学在距离某建筑物6米的点A处测得广告牌B点、C点的仰角分别为52°和35°,则广告牌的高度BC为_____________米(精确到0.1米).(sin35°≈0.57,cos35°≈0.82,tan35°≈0.70;sin52°≈0.79,cos52°≈0.62,tan52°≈1.28)
8. (2009荆门)=______.
9. (2009义乌)(1) 计算=
10. (2009湖州)(1)计算:=
五、课后练习
1.(2010辽宁丹东市)如图,小颖利用有一个锐角是30°的三角板测量一棵树
的高度,已知她与树之间的水平距离BE为5m,AB为1.5m
(即小颖的眼睛距地面的距离),那么这棵树高是( )
A.()m B.()m C. m D.4m
2.(2010山东日照)如图,在等腰Rt△ABC中,∠C=90o,AC=6,D是AC上一点,若tan∠DBA=,则AD的长为
(A) 2 (B) (C) (D)1
3.(2010四川凉山)已知在中,,设,当是最小的内角时,的取值范围是
A. B. C. D.
4.(2010四川眉山)如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为( )
A.90° B.60° C.45° D.30°
5.(2010 浙江省温州)如图,已知一商场自动扶梯的长z为10米,该自动扶梯到达的高度h为6米,自动扶梯与地面所成的角为θ,则tanθ的值等于( )
6.(2010 浙江台州市)如图,矩形ABCD中,AB>AD,AB=a,AN平分∠DAB,DM⊥AN于点M,CN⊥AN于点N.则DM+CN的值为(用含a的代数式表示)( )
A.a B. C. D.
7.(2010 黄冈)在△ABC中,∠C=90°,sinA=,则tanB=( )
A. B. C. D.
8.(2010年贵州毕节)在正方形网格中,的位置如图所示,则的值为( )
A. B. C. D.
9.(2010湖北荆门)计算sin45°的结果等于( )
A. B.1 C. D.
10.(2010湖南常德)在Rt△ABC中,∠C=90°,若AC=2BC,则sin A的值是( )
A. B.2 C. D.
11.(2010江苏常州)在Rt△ABC中,∠C=90°,AC=2,BC=1,则tanB= ,sinA= 。
12.(2010山东潍坊)直角梯形ABCD中,AB⊥BC,AD∥BC,BC>AD,AD=2,AB=4,点E在AB上,将△CBE沿CE翻折,使得B点与D点重合,则∠BCE的正切值为 .
21世纪教育网 ( http: / / www.21cnjy.com / )
13.(2010广东中山)如图,已知RtΔABC中,斜边BC上的高AD=4,cosB=,则AC= .
14.(2010湖南怀化)在Rt△ABC中,∠C=90°,sinA=,则∠A= .
15.(2010湖北荆州)如图,在△ABC中,∠B=45°,cos∠C=,AC=5a,则△ABC的面积用含a的式子表示是 .
16.如图,某边防巡逻队在一个海滨浴场岸边的A点处发现海中的B点有人求救,便立即派三名救生员前去营救.1号救生员从A点直接跳入海中;2号救生员沿岸边(岸边看成是直线)向前跑到C点,再跳入海中;3号救生员沿岸边向前跑3 0 O米到离B点最近的D点,再跳人海中.救生员在岸上跑的速度都是6米/秒,在水中游泳的速度都是2米/秒.若∠BAD=4 5°,∠BCD=6 0°,三名救生员同时从A点出发,请说明谁先到达营救地点B. (参考数据≈1.4,≈1.7)
17.如图13,某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离是1.7m,看旗杆顶部的仰角为;小红的眼睛与地面的距离是1.5m,看旗杆顶部的仰角为.两人相距28米且位于旗杆两侧(点在同一条直线上).请求出旗杆的高度.(参考数据:,,结果保留整数)
18.小刚有一块含有30°角的直角三角板,他想测量其短直角边的长度,而手中另外只有一个量角器,于是他采用了如下的办法,并获得了相关数据:
第一步,他先用三角板标有刻度的一边测出量角器的直径AB的长度为9cm;
第二步,将三角板与量角器按如图所示的方式摆放,并量得∠BOC为80°(O为AB中点).
请你根据小刚测得的数据,求出三角板的短直角边AC的长.
(参考数据:sin80°=0.98,cos80°=0.17,tan80°=5.67;sin40°=0.64,cos40°=0.77,tan40°=0.84,结果精确到0.1cm.)
A
B
C
D
E
图4
A
C
B
图1
A
B
C
D
O
例2
A
C
B
A
B
O
例7
A
B
O
6
8
C
E
A
B
D
(第6题)
(第7题)
A
B
C
D
E
)
45°
图1
C
D
B
A
图2
A
B
O
北
东
西
南
图3
)
55°
B
C
A
(第1题)
图10
图9
A
B
C
D
6米
52°
35°
(第14题图)
B
A
E
D
C
30°
(第6题)
M
N
BO
A
DO
C
30°
45°
A
B
C
O
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
