平行线的特征2

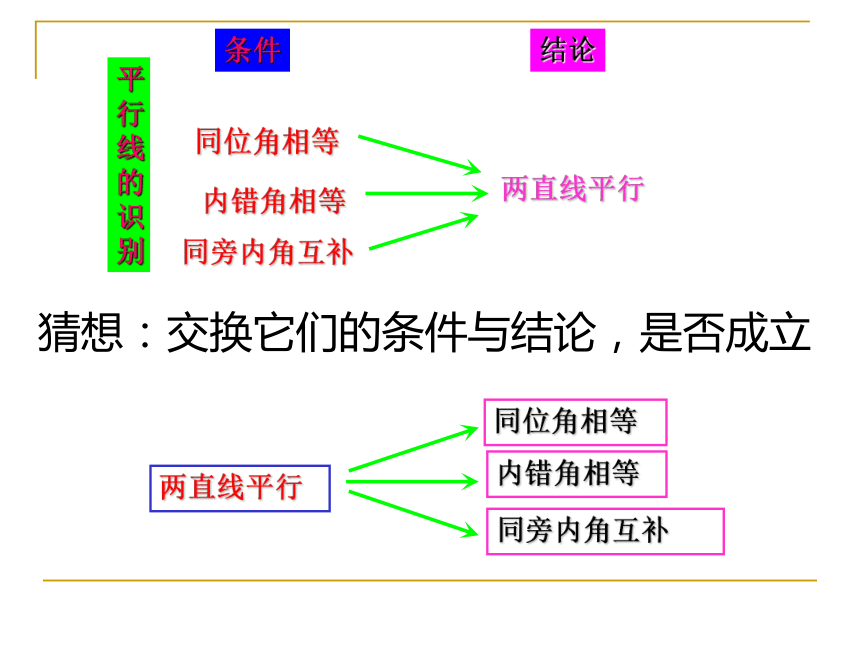
课件24张PPT。32条件结论两直线平行同位角相等内错角相等同旁内角互补平行线的识别同位角相等内错角相等同旁内角互补两直线平行猜想：交换它们的条件与结论，是否成立做一做，想一想活动：请同学先画出两条平行线，再画一条直线与他们相交（如图） :将相关的角（如同位角、内错角）剪下，然后把这个角与相应的角进行比较，看是否重合，即这两个角的大小是否相等。或用量角器度量.
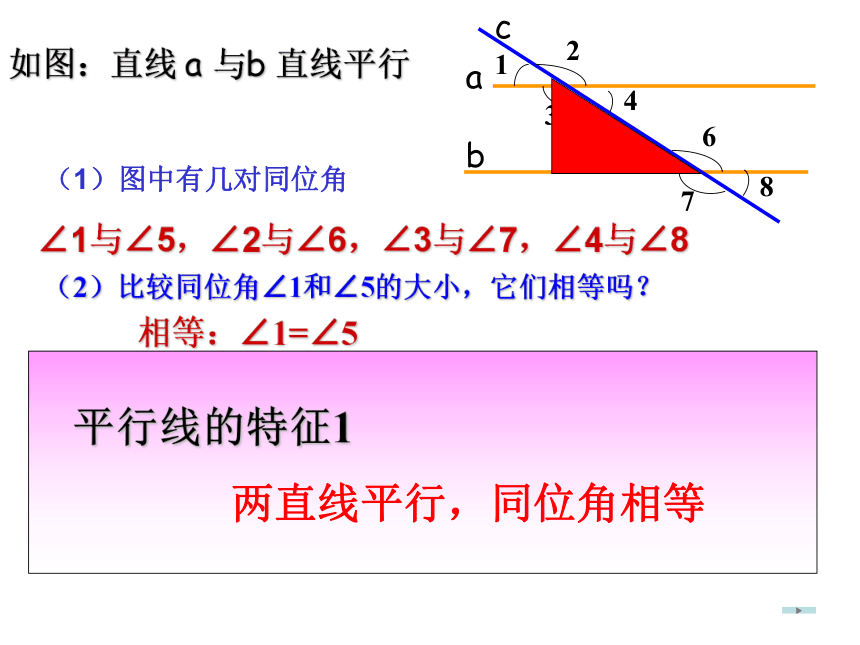
注意识别同位角、内错角和同旁内角。如图：直线 a 与b 直线平行（2）比较同位角∠1和∠5的大小，它们相等吗？相等：∠1=∠5∠2=∠6∠3=∠7∠4=∠8还有三对同位角，它们的大小有什么关系？（1）图中有几对同位角∠1与∠5，∠2与∠6，∠3与∠7，∠4与∠8
平行线的特征1两直线平行，同位角相等分组讨论：abc123456782、图中有几对内错角，它们的大小有什么关系，你有什么方法可以进行比较？
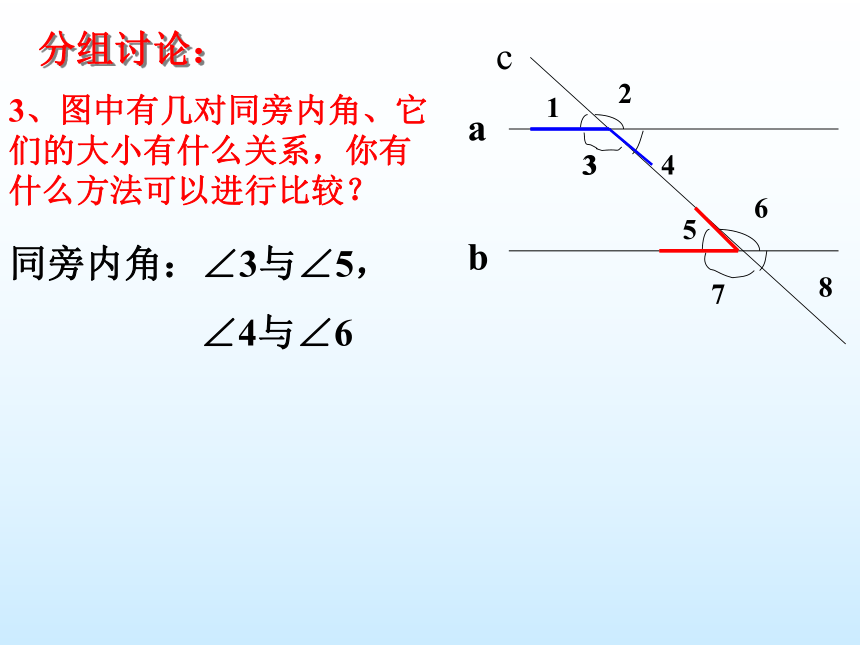
3内错角： ∠4与∠5 ，∠3与∠6，相等关系：∠4＝∠5，两直线平行，内错角相等∵ a ∥b（已知）∵∠1=∠4（对顶角相等）∴ ∠4=∠5（等量代换）∴ ∠1=∠5（两直线平行，同位角相等）分组讨论：abc123456783、图中有几对同旁内角、它们的大小有什么关系，你有什么方法可以进行比较？3同旁内角：∠3与∠5，
∠4与∠6分组讨论：abc123456783、图中有几对同旁内角、它们的大小有什么关系，你有什么方法可以进行比较？3同旁内角：∠3＋∠5＝180，
∠4＋∠6＝180同旁内角：∠3与∠5，∠4与∠6∴ ∠1=∠5（两直线平行，同位角相等）∵ a ∥b（已知）又∵∠1+∠3=180°（平角的定义）∴ ∠3+∠5=180°（等量代换）两直线平行，同旁内角互补已知两条平行线被第三条直线所截,
其中的同位角、内错角、同旁内角的关系如何? 两直线平行 同位角相等内错角相等同旁内角互补两直线平行 同位角相等内错角相等同旁内角互补平行线的识别平行线的特征线的关系角的关系特征角的关系线的关系识别理一理试一试：1、∵ AD//BC (已知)
∴ ∠B=∠1 ( )
2、∵ AB//CD (已知)
∴ ∠D＝∠1 ( )
3、∵ AD//BC (已知)
∴ ∠C＋ ＝180? ( )1两直线平行，同位角相等两直线平行，内错角相等两直线平行，同旁内角互补∠D例1 如图，已知直线a∥b，
∠1=50°，求∠2的度数。 解： ∵ a∥b
∴ ∠1=∠2（ )两直线平行，内错角相等 ∵ ∠1=50° ∴ ∠2=50° （已知）(已知)（等量代换）5例1 如图，已知直线a∥b，
∠1=50°，求∠3的度数。 解： ∵ a∥b
∴ ∠3=∠1（ )两直线平行，同位角相等(已知)（等量代换）例1 如图，已知直线a∥b，
∠1=50°，求∠5的度数。 解： ∵ a∥b
∴ ∠1+∠5=180° （ )两直线平行，同旁内角互补 ∵ ∠1=50° ∴ ∠5=130° （已知）(已知)（等量代换）345∠4＝∠5= 130°（对顶角相等） 两条平行线被第三条直线所截的八个角，
已知一个，可以求出其余的七个
回忆求角的方法例2：如图，在四边形ABCD中，已知AB//CD，
∠B＝60?，求∠C 的度数。能否求得∠A的度数？解：∵AB//CD (已知) ∴∠B＋∠C＝180°
(两直线平行, 同旁内角互补)∵∠B＝60°（已知）∴ ∠C＝120 °（等式的性质）根据已知条件，无法求得∠A的度数。两条直线被第三条直线所截,同旁内角互
补?练习
如图．（1） ∵ AD∥BC， ∴ ____+∠ABC =180°(两直线平行，同 旁内角互补)；（2） ∵ AB∥CD，∴ ____+∠ABC =180°∠BAD∠BCD(两直线平行，同旁内角互补)；　1、如图某玻璃碎片是梯形，已有上底的一部分，量得∠A=115°，∠D＝100°，梯形另外两个角各是多少度？解：∵AD∥BC（已知）∴∠A+∠B=180o∠C=180o－100o=80o∴梯形的另外两个角分别是65o和80o。（两直线平行，同旁内角互补）　∴∠B=180o－115o=65o∠D+∠C=180o（两直线平行，同旁内角互补）∵ ∠A=115°，∠D=100°（已知）生活数学（等式的性质）练习
画出将如图所示的方格纸中的图形向
右平移3格，并向下平移4格后的图形。 如图：一束平行光线AB和DE射向一个水平镜面后被发射，此时∠1=∠2 ， ∠3=∠4 。（1 ）∠1，∠3的大小有什么关系？
(2)反射光线BC与EF也平行吗？
如图：一束平行光线AB和DE射向一个水平镜面后被发射，此时∠1=∠2 ， ∠3=∠4 。1234BEACDF（1 ）∠1，∠3的大小有什么关系？∠2与∠4呢？∵AB∥DE ∴∠1=∠3相等你知道理由吗？两直线平行
同位角相等（2 ）发射光线BC与EF也平行吗？∵ ∠2=∠4 ∴ BC∥EF 平行同位角相等
两直线平行∵ ∠1=∠3 且 ∠1=∠2 ，∠3=∠4(已知)∴ ∠2=∠4 (等量代换)CCC我是这样思考：
（1）AB//DE ∠ 1= ∠ 3 ∠ 2= ∠ 4;
(2) ∠ 2= ∠ 4 BC//EF；本节课你学到了什么?小结 本节课学习了平行线的三个特征(性质) ，总结了平行线的识别与特征的区别．
识别：角的关系 平行关系
特征：平行关系 角的关系
本节课初步学习了如何应用平行线的识别与特征进行计算和说理(证明)．
要懂得几何中的计算往往要说理，要熟悉几何里计算题的格式；在推理的过程中,要能清楚每一步的依据
www.czsx.com.cn比较练习
一、???? 看右图，填空。
（1）因为AB//CD,所以∠1＝ ，∠2＝ ，∠3＝ ，∠4＝ ，理由是____________________________________。
（2）因为∠1＝∠5，所以AB// ,理由是
。
3）因为AB//CD,所以∠2＝∠7，∠4＝∠5，
理由是 。（4）因为∠2＝∠7，∠4＝∠5，所以AB//CD, 理由是 。
（5）因为AB//CD,所以∠2＋∠ ＝180°，∠4＋∠ ＝180°，理由是 。
（6）因为∠2＋∠5＝180°，所以 // ，理由是 。
CDABCD15427386∠5∠6∠7∠8同位角 相 等，两直线平行。两直线平行，内错角相等。内错角相等，两直线平行。57两直线平行，同旁内角互补。ABCD同旁内角互补，两直线平行。两直线平行，同位角相等