人教A版必修2《第一章空间几何体》综合试题及答案
文档属性
| 名称 | 人教A版必修2《第一章空间几何体》综合试题及答案 |

|
|
| 格式 | rar | ||
| 文件大小 | 116.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-03-16 00:00:00 | ||
图片预览


文档简介
人教A必修2第一章空间几何体综合试题
一、选择题(每道题5分)
1.有一个几何体的三视图如下图所示,这个几何体可能是一个( ).
主视图 左视图 俯视图
(第1题)
A.棱台 B.棱锥 C.棱柱 D.正八面体
2.如果一个水平放置的平面 图形的斜二测直观图是一个底角为45°,腰和上底均为的等腰梯形,那么原平面图形的面积是( ).
A.2+ B. C. D.
3.棱长都是的三棱锥的表面积为( ).
A. B.2 C.3 D.4
4.长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在同一球面上,则这个球的表面积是( ).
A.25π B.50π C.125π D.都不对
5.正方体的棱长和外接球的半径之比为( ).
A.∶1 B.∶2 C.2∶ D.∶3
6.在△ABC中,AB=2,BC=1.5,∠ABC=120°,若使△ABC绕直线旋转一周,则所形成的几何体的体积是( ).
A.π B.π C.π D.π
7.若底面是菱形的棱柱其侧棱垂直于底面,且侧棱长为5,它的对角线的长分别是9和15,则这个棱柱的侧面积是( ).
A.130 B.140 C.150 D.160
8.半径为的半圆卷成一个圆锥,则它的体积为( )
A. B. C. D.
9.下列关于用斜二测画法画直观图的说法中,错误的是( ).
A.用斜二测画法画出的直观图是在平行投影下画出的空间图形
B.几何体的直观图的长、宽、高与其几何体的长、宽、高的比例相同
C.水平放置的矩形的直观图是平行四边形
D.水平放置的圆的直观图是椭圆
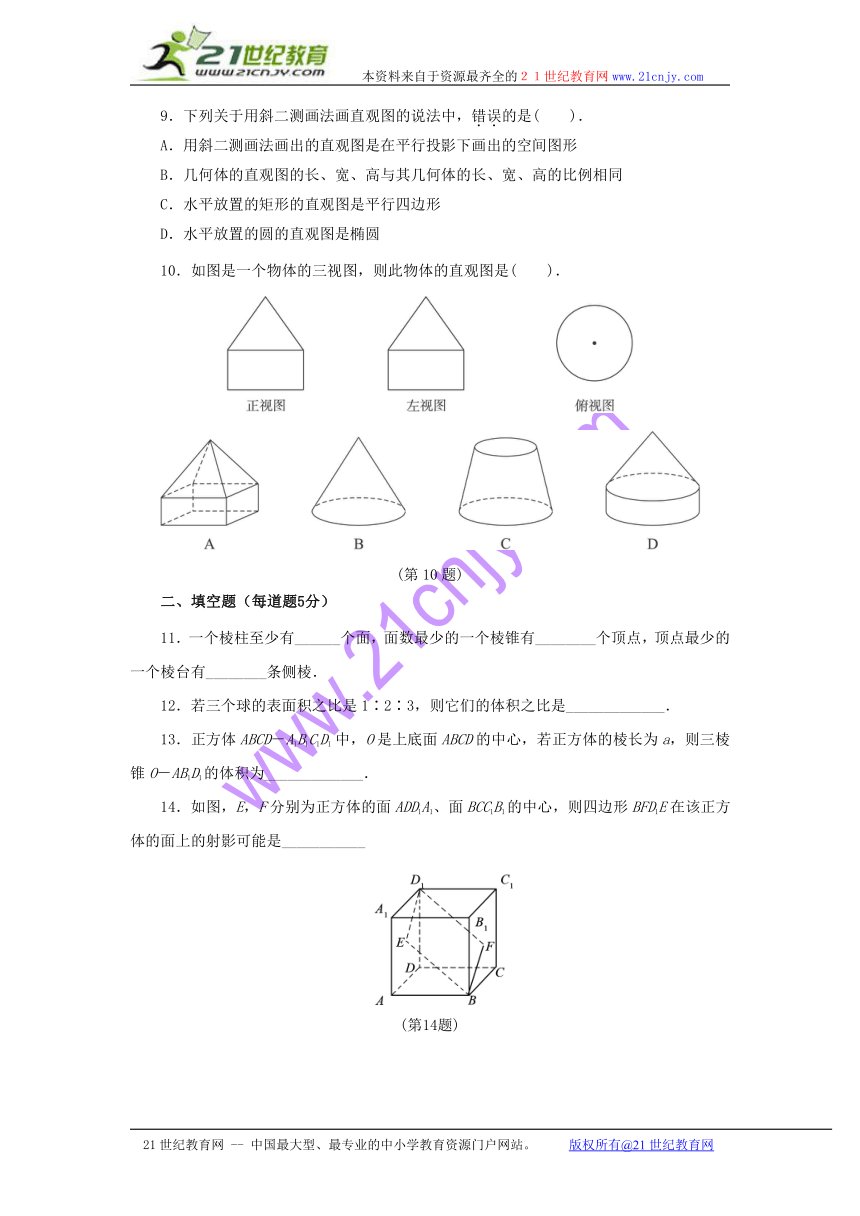
10.如图是一个物体的三视图,则此物体的直观图是( ).
(第10题)
二、填空题(每道题5分)
11.一个棱柱至少有______个面,面数最少的一个棱锥有________个顶点,顶点最少的一个棱台有________条侧棱.
12.若三个球的表面积之比是1∶2∶3,则它们的体积之比是_____________.
13.正方体ABCD-A1B1C1D1 中,O是上底面ABCD的中心,若正方体的棱长为a,则三棱锥O-AB1D1的体积为_____________.
14.如图,E,F分别为正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是___________
(第14题)
15.已知一个长方体共一顶点的三个面的面积分别是、、,则这个长方体的对角线长是___________,它的体积为___________.
16.一个直径为32厘米的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高9厘米则此球的半径为_________厘米.
三、解答题(17题,18,19各15分;20题25分)
17.有一个正四棱台形状的油槽,可以装油190 L,假如它的两底面边长分别等于60 cm和40 cm,求它的深度.
18.如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.
(第18题)
19.已知圆台的上下底面半径分别是,且侧面面积等于两底面面积之和,求该圆台的母线长.
20.养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12 m,高4 m,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大4 m(高不变);二是高度增加4 m(底面直径不变).
(1)分别计算按这两种方案所建的仓库的体积;
(2)分别计算按这两种方案所建的仓库的表面积;
(3)哪个方案更经济些?
第一章 空间几何体
参考答案
一、选择题
1.A
解析:从俯视图来看,上、下底面都是正方形,但是大小不一样,可以判断可能是棱台.
2.A
解析:原图形为一直角梯形,其面积S=(1++1)×2=2+.
3.A
解析:因为四个面是全等的正三角形,则S表面=4×=.
4.B
解析:长方体的对角线是球的直径,
l==5,2R=5,R=,S=4πR2=50π.
5.C
解析:正方体的对角线是外接球的直径.
6.D
解析:V=V大-V小=πr2(1+1.5-1)=π.
7.D
解析:设底面边长是a,底面的两条对角线分别为l1,l2,而=152-52,=92-52,
而+=4a2,即152-52+92-52=4a2,a=8,S侧面=4×8×5=160.
8.A
9.B
解析:斜二测画法的规则中,已知图形中平行于 x 轴的线段,在直观图中保持原长度不变;平行于 y 轴的线段,长度为原来的一半.平行于 z 轴的线段的平行性和长度都不变.
10.D
解析:从三视图看底面为圆,且为组合体,所以选D.
二、填空题
11.参考答案:5,4,3.
解析:符合条件的几何体分别是:三棱柱,三棱锥,三棱台.
12.参考答案:1∶2∶3.
r1∶r2∶r3=1∶∶,∶∶=13∶()3∶()3=1∶2∶3.
13.参考答案:.
解析:画出正方体,平面AB1D1与对角线A1C的交点是对角线的三等分点,
三棱锥O-AB1D1的高h=a,V=Sh=××2a2×a=a3.
另法:三棱锥O-AB1D1也可以看成三棱锥A-OB1D1,它的高为AO,等腰三角形OB1D1为底面.
14.参考答案:平行四边形或线段.
15.参考答案:,.
解析:设ab=,bc=,ac=,则V = abc=,c=,a=,b=1,
l==.
16.参考答案:12.
解析:V=Sh=πr2h=πR3,R==12.
三、解答题
17.参考答案:
V=(S++S)h,h===75.
18.参考答案:
S表面=S下底面+S台侧面+S锥侧面
=π×52+π×(2+5)×5+π×2×2
=(60+4)π.
V=V台-V锥
=π(+r1r2+)h-πr2h1
=π.
19.解
20.
解:(1) 参考答案:如果按方案一,仓库的底面直径变成16 m,则仓库的体积
V1=Sh=×π×()2×4=π(m3).
如果按方案二,仓库的高变成8 m,则仓库的体积
V2=Sh=×π×()2×8=π(m3).
(2) 参考答案:如果按方案一,仓库的底面直径变成16 m,半径为8 m.
棱锥的母线长为l==4,
仓库的表面积S1=π×8×4=32π(m2).
如果按方案二,仓库的高变成8 m.
棱锥的母线长为l==10,
仓库的表面积S2=π×6×10=60π(m2).
(3) 参考答案:∵V2>V1,S2<S1,∴方案二比方案一更加经济些.
一、选择题(每道题5分)
1.有一个几何体的三视图如下图所示,这个几何体可能是一个( ).
主视图 左视图 俯视图
(第1题)
A.棱台 B.棱锥 C.棱柱 D.正八面体
2.如果一个水平放置的平面 图形的斜二测直观图是一个底角为45°,腰和上底均为的等腰梯形,那么原平面图形的面积是( ).
A.2+ B. C. D.
3.棱长都是的三棱锥的表面积为( ).
A. B.2 C.3 D.4
4.长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在同一球面上,则这个球的表面积是( ).
A.25π B.50π C.125π D.都不对
5.正方体的棱长和外接球的半径之比为( ).
A.∶1 B.∶2 C.2∶ D.∶3
6.在△ABC中,AB=2,BC=1.5,∠ABC=120°,若使△ABC绕直线旋转一周,则所形成的几何体的体积是( ).
A.π B.π C.π D.π
7.若底面是菱形的棱柱其侧棱垂直于底面,且侧棱长为5,它的对角线的长分别是9和15,则这个棱柱的侧面积是( ).
A.130 B.140 C.150 D.160
8.半径为的半圆卷成一个圆锥,则它的体积为( )
A. B. C. D.
9.下列关于用斜二测画法画直观图的说法中,错误的是( ).
A.用斜二测画法画出的直观图是在平行投影下画出的空间图形
B.几何体的直观图的长、宽、高与其几何体的长、宽、高的比例相同
C.水平放置的矩形的直观图是平行四边形
D.水平放置的圆的直观图是椭圆
10.如图是一个物体的三视图,则此物体的直观图是( ).
(第10题)
二、填空题(每道题5分)
11.一个棱柱至少有______个面,面数最少的一个棱锥有________个顶点,顶点最少的一个棱台有________条侧棱.
12.若三个球的表面积之比是1∶2∶3,则它们的体积之比是_____________.
13.正方体ABCD-A1B1C1D1 中,O是上底面ABCD的中心,若正方体的棱长为a,则三棱锥O-AB1D1的体积为_____________.
14.如图,E,F分别为正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是___________
(第14题)
15.已知一个长方体共一顶点的三个面的面积分别是、、,则这个长方体的对角线长是___________,它的体积为___________.
16.一个直径为32厘米的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高9厘米则此球的半径为_________厘米.
三、解答题(17题,18,19各15分;20题25分)
17.有一个正四棱台形状的油槽,可以装油190 L,假如它的两底面边长分别等于60 cm和40 cm,求它的深度.
18.如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.
(第18题)
19.已知圆台的上下底面半径分别是,且侧面面积等于两底面面积之和,求该圆台的母线长.
20.养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12 m,高4 m,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大4 m(高不变);二是高度增加4 m(底面直径不变).
(1)分别计算按这两种方案所建的仓库的体积;
(2)分别计算按这两种方案所建的仓库的表面积;
(3)哪个方案更经济些?
第一章 空间几何体
参考答案
一、选择题
1.A
解析:从俯视图来看,上、下底面都是正方形,但是大小不一样,可以判断可能是棱台.
2.A
解析:原图形为一直角梯形,其面积S=(1++1)×2=2+.
3.A
解析:因为四个面是全等的正三角形,则S表面=4×=.
4.B
解析:长方体的对角线是球的直径,
l==5,2R=5,R=,S=4πR2=50π.
5.C
解析:正方体的对角线是外接球的直径.
6.D
解析:V=V大-V小=πr2(1+1.5-1)=π.
7.D
解析:设底面边长是a,底面的两条对角线分别为l1,l2,而=152-52,=92-52,
而+=4a2,即152-52+92-52=4a2,a=8,S侧面=4×8×5=160.
8.A
9.B
解析:斜二测画法的规则中,已知图形中平行于 x 轴的线段,在直观图中保持原长度不变;平行于 y 轴的线段,长度为原来的一半.平行于 z 轴的线段的平行性和长度都不变.
10.D
解析:从三视图看底面为圆,且为组合体,所以选D.
二、填空题
11.参考答案:5,4,3.
解析:符合条件的几何体分别是:三棱柱,三棱锥,三棱台.
12.参考答案:1∶2∶3.
r1∶r2∶r3=1∶∶,∶∶=13∶()3∶()3=1∶2∶3.
13.参考答案:.
解析:画出正方体,平面AB1D1与对角线A1C的交点是对角线的三等分点,
三棱锥O-AB1D1的高h=a,V=Sh=××2a2×a=a3.
另法:三棱锥O-AB1D1也可以看成三棱锥A-OB1D1,它的高为AO,等腰三角形OB1D1为底面.
14.参考答案:平行四边形或线段.
15.参考答案:,.
解析:设ab=,bc=,ac=,则V = abc=,c=,a=,b=1,
l==.
16.参考答案:12.
解析:V=Sh=πr2h=πR3,R==12.
三、解答题
17.参考答案:
V=(S++S)h,h===75.
18.参考答案:
S表面=S下底面+S台侧面+S锥侧面
=π×52+π×(2+5)×5+π×2×2
=(60+4)π.
V=V台-V锥
=π(+r1r2+)h-πr2h1
=π.
19.解
20.
解:(1) 参考答案:如果按方案一,仓库的底面直径变成16 m,则仓库的体积
V1=Sh=×π×()2×4=π(m3).
如果按方案二,仓库的高变成8 m,则仓库的体积
V2=Sh=×π×()2×8=π(m3).
(2) 参考答案:如果按方案一,仓库的底面直径变成16 m,半径为8 m.
棱锥的母线长为l==4,
仓库的表面积S1=π×8×4=32π(m2).
如果按方案二,仓库的高变成8 m.
棱锥的母线长为l==10,
仓库的表面积S2=π×6×10=60π(m2).
(3) 参考答案:∵V2>V1,S2<S1,∴方案二比方案一更加经济些.
