指数函数教案
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
中心中学竞教课教案
指
数
函
数
教 师:高 红 均
课 题:§2.6.1指数函数
授课类型:新授课
教学目的:
㈠知识目标
1、指数函数的概念.
2、指数函数的图象、性质.
㈡能力目标
1、理解指数函数的概念.
2、掌握指数函数的图象、性质.
3、培养学生实际应用函数的能力.
㈢情感目标
1、认识事物之间的普遍联系与相互转化.
2、用联系的观点看问题.
3、了解数学知识在生产生活中的应用.
教学重点:指数函数的图象、性质.
教学难点:指数函数的图象性质与底数a的关系.
教学方法:学导式
教 具:多媒体
教学过程:
㈠复习引入(8分钟)
我们前面学习了指数运算,在此基础上,今天我们要来研究一类新的常见函数-------指数函数.
1.6.指数函数(板书)
这类函数之所以重点介绍的原因就是它是实际生活中的一种需要.比如我们看下面的问题:
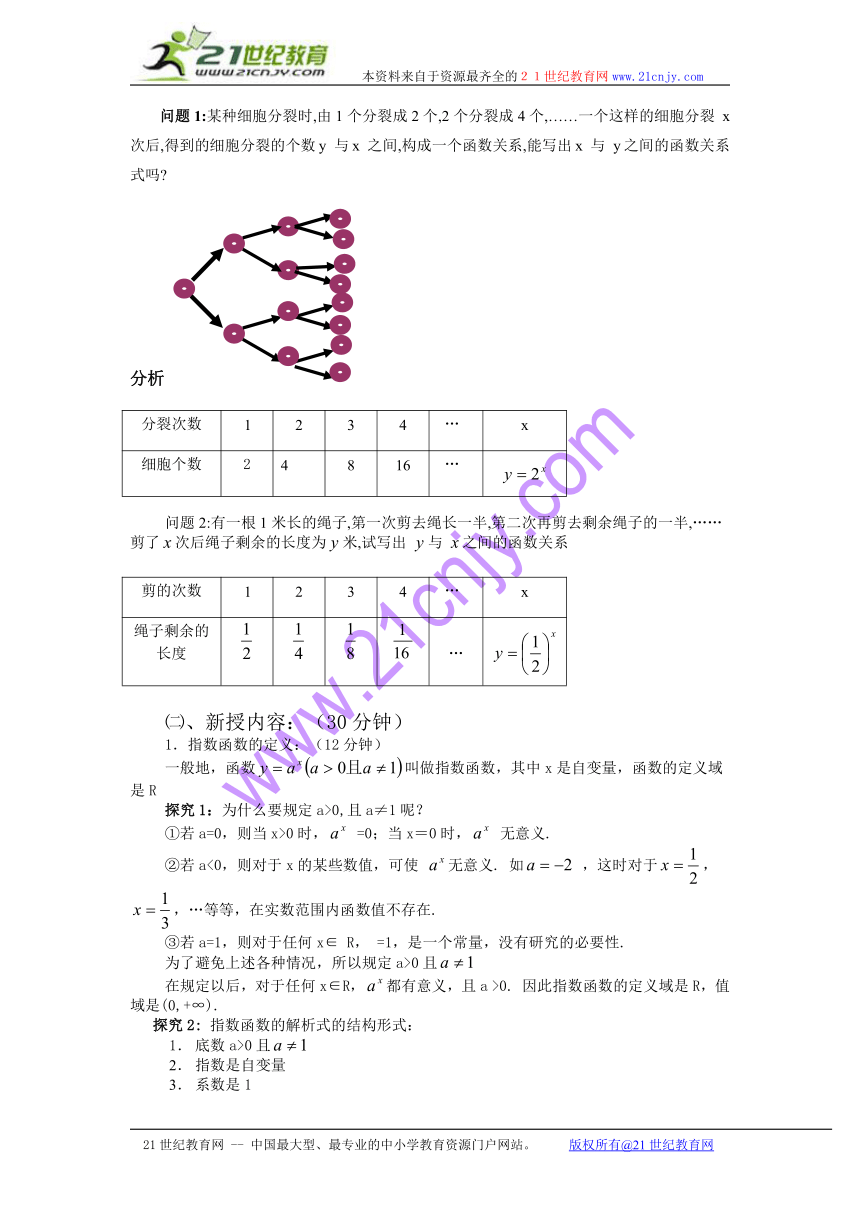
问题1:某种细胞分裂时,由1个分裂成2个,2个分裂成4个,……一个这样的细胞分裂 x次后,得到的细胞分裂的个数y 与x 之间,构成一个函数关系,能写出x 与 y之间的函数关系式吗
分析
分裂次数 1 2 3 4 … x
细胞个数 2 4 8 16 …
剪的次数 1 2 3 4 … x
绳子剩余的长度 …
问题2:有一根1米长的绳子,第一次剪去绳长一半,第二次再剪去剩余绳子的一半,……剪了次后绳子剩余的长度为米,试写出 与 之间的函数关系
㈡、新授内容:(30分钟)
1.指数函数的定义:(12分钟)
一般地,函数叫做指数函数,其中x是自变量,函数的定义域是R
探究1:为什么要规定a>0,且a≠1呢?
①若a=0,则当x>0时, =0;当x=0时, 无意义.
②若a<0,则对于x的某些数值,可使 无意义. 如 ,这时对于, ,…等等,在实数范围内函数值不存在.
③若a=1,则对于任何x∈ R, =1,是一个常量,没有研究的必要性.
为了避免上述各种情况,所以规定a>0且
在规定以后,对于任何x∈R,都有意义,且a >0. 因此指数函数的定义域是R,值域是(0,+∞).
探究2: 指数函数的解析式的结构形式:
1. 底数a>0且
2. 指数是自变量
3. 系数是1
例1 已知是指数函数,求a的取值范围。
解:由题意得: ①
②
解①得:
解②得:
∴a的取值范围为
练习:下列函数中哪些是指数函数?
(1) (2)
(3) (4)
(5) (6)
(7) (8) ()
(9) (10)
解:(1)(5)(8)是指数函数
评述:例1及练习的设计意图为让学生熟悉指数函数的结构形式
有些函数貌似指数函数,实际上却不是,如y=+k (a>0且a≠1,k∈Z);有些函数看起来不像指数函数,实际上却是,如y= (a>0且a≠1),因为它可以化为y=,其中a >0,且a≠1。
2.指数函数的图象和性质:(18分钟)
画出的图象和的图象
1
x … -2 -1 0 1 2 …
… 1 2 4 …
… 4 2 1 …
【学生活动】
观察的图象,从以下几个方面找的性质
(1)定义域
(2)值域
(3)特殊点
(4)单调性
再观察的图象,也从以上几个方面找的性质
【师】总结的性质:
a>1 0(1)定义域为R
(2)值域为
(3)过定点(0,1)
(4)在R上是增函数 (4)在R上是减函数
例2 利用指数函数的单调性比较下列各式中几个式子的大小:
(1)
(2)
解:(1)
(2)
即
评述:本题是指数函数的单调性的应用。会利用函数的单调性比较熟的大小是本节课教学目标之一。
练习:已知下列不等式,比较m和n的大小
(1)
(2)
(3)
例3 某种放射性物质不断变化为其他物质,每经过1年剩留的这种物质是原来的84%,画出这种物质的剩留量随时间变化的图象,并从图象上求出经过多少年,剩量留是原来的一半(结果保留1个有效数字)
分析:通过恰当假设,将剩留量y表示成经过年数x的函数,并可列表、描点、作图,进而求得所求
解:设这种物质量初的质量是1,经过x年,剩留量是y
经过1年,剩留量y=1×84%=0.841;
经过2年,剩留量y=0.841×84%=0.842;
……
一般地,经过x年,剩留量 y=(0.84 )x
根据这个函数关系式可以列表如下:
x 0 1 2 3 4 5 6
y 1 0.84 0.71 0.59 0.50 0.42 0.35
用描点法画出指数函数y=0.84x的图象 从图上看出y=0.5只需x≈4.
答:约经过4年,剩留量是原来的一半
评述:本题是指数函数图象的应用;数形结合思想的体现
(三) 小 结 (3分钟)
本节课学习了以下内容:指数函数概念,指数函数的图象和性质。通过本节课的学习,大家要能在理解指数函数的概念的基础上,掌握指数函数的图象和性质,并会简单的应用。
(四)课后作业:(2分钟)
习题2.6 1 ,3
板书设计
§2.6.1 指数函数
1.指数函数的定义 2.指数函数的 3.例题讲解 4.学生练习
图象和性质 【例1】
【例2】
教学后记
由于指数函数是一个新的函数类型,学生初次接触,在接受起来有一定的难度。但是指数函数是在学习了指数的有关概念和幂的运算性质的基础上建立起来的函数模型,减轻了学习的难度。从作业情况看,学生的掌握情况得比较好。但是也还存在一些问题,特别是对指数函数的图象和性质的掌握情况还不够好,在后面的学习中应加强。
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
中心中学竞教课教案
指
数
函
数
教 师:高 红 均
课 题:§2.6.1指数函数
授课类型:新授课
教学目的:
㈠知识目标
1、指数函数的概念.
2、指数函数的图象、性质.
㈡能力目标
1、理解指数函数的概念.
2、掌握指数函数的图象、性质.
3、培养学生实际应用函数的能力.
㈢情感目标
1、认识事物之间的普遍联系与相互转化.
2、用联系的观点看问题.
3、了解数学知识在生产生活中的应用.
教学重点:指数函数的图象、性质.
教学难点:指数函数的图象性质与底数a的关系.
教学方法:学导式
教 具:多媒体
教学过程:
㈠复习引入(8分钟)
我们前面学习了指数运算,在此基础上,今天我们要来研究一类新的常见函数-------指数函数.
1.6.指数函数(板书)
这类函数之所以重点介绍的原因就是它是实际生活中的一种需要.比如我们看下面的问题:
问题1:某种细胞分裂时,由1个分裂成2个,2个分裂成4个,……一个这样的细胞分裂 x次后,得到的细胞分裂的个数y 与x 之间,构成一个函数关系,能写出x 与 y之间的函数关系式吗
分析
分裂次数 1 2 3 4 … x
细胞个数 2 4 8 16 …
剪的次数 1 2 3 4 … x
绳子剩余的长度 …
问题2:有一根1米长的绳子,第一次剪去绳长一半,第二次再剪去剩余绳子的一半,……剪了次后绳子剩余的长度为米,试写出 与 之间的函数关系
㈡、新授内容:(30分钟)
1.指数函数的定义:(12分钟)
一般地,函数叫做指数函数,其中x是自变量,函数的定义域是R
探究1:为什么要规定a>0,且a≠1呢?
①若a=0,则当x>0时, =0;当x=0时, 无意义.
②若a<0,则对于x的某些数值,可使 无意义. 如 ,这时对于, ,…等等,在实数范围内函数值不存在.
③若a=1,则对于任何x∈ R, =1,是一个常量,没有研究的必要性.
为了避免上述各种情况,所以规定a>0且
在规定以后,对于任何x∈R,都有意义,且a >0. 因此指数函数的定义域是R,值域是(0,+∞).
探究2: 指数函数的解析式的结构形式:
1. 底数a>0且
2. 指数是自变量
3. 系数是1
例1 已知是指数函数,求a的取值范围。
解:由题意得: ①
②
解①得:
解②得:
∴a的取值范围为
练习:下列函数中哪些是指数函数?
(1) (2)
(3) (4)
(5) (6)
(7) (8) ()
(9) (10)
解:(1)(5)(8)是指数函数
评述:例1及练习的设计意图为让学生熟悉指数函数的结构形式
有些函数貌似指数函数,实际上却不是,如y=+k (a>0且a≠1,k∈Z);有些函数看起来不像指数函数,实际上却是,如y= (a>0且a≠1),因为它可以化为y=,其中a >0,且a≠1。
2.指数函数的图象和性质:(18分钟)
画出的图象和的图象
1
x … -2 -1 0 1 2 …
… 1 2 4 …
… 4 2 1 …
【学生活动】
观察的图象,从以下几个方面找的性质
(1)定义域
(2)值域
(3)特殊点
(4)单调性
再观察的图象,也从以上几个方面找的性质
【师】总结的性质:
a>1 0
(2)值域为
(3)过定点(0,1)
(4)在R上是增函数 (4)在R上是减函数
例2 利用指数函数的单调性比较下列各式中几个式子的大小:
(1)
(2)
解:(1)
(2)
即
评述:本题是指数函数的单调性的应用。会利用函数的单调性比较熟的大小是本节课教学目标之一。
练习:已知下列不等式,比较m和n的大小
(1)
(2)
(3)
例3 某种放射性物质不断变化为其他物质,每经过1年剩留的这种物质是原来的84%,画出这种物质的剩留量随时间变化的图象,并从图象上求出经过多少年,剩量留是原来的一半(结果保留1个有效数字)
分析:通过恰当假设,将剩留量y表示成经过年数x的函数,并可列表、描点、作图,进而求得所求
解:设这种物质量初的质量是1,经过x年,剩留量是y
经过1年,剩留量y=1×84%=0.841;
经过2年,剩留量y=0.841×84%=0.842;
……
一般地,经过x年,剩留量 y=(0.84 )x
根据这个函数关系式可以列表如下:
x 0 1 2 3 4 5 6
y 1 0.84 0.71 0.59 0.50 0.42 0.35
用描点法画出指数函数y=0.84x的图象 从图上看出y=0.5只需x≈4.
答:约经过4年,剩留量是原来的一半
评述:本题是指数函数图象的应用;数形结合思想的体现
(三) 小 结 (3分钟)
本节课学习了以下内容:指数函数概念,指数函数的图象和性质。通过本节课的学习,大家要能在理解指数函数的概念的基础上,掌握指数函数的图象和性质,并会简单的应用。
(四)课后作业:(2分钟)
习题2.6 1 ,3
板书设计
§2.6.1 指数函数
1.指数函数的定义 2.指数函数的 3.例题讲解 4.学生练习
图象和性质 【例1】
【例2】
教学后记
由于指数函数是一个新的函数类型,学生初次接触,在接受起来有一定的难度。但是指数函数是在学习了指数的有关概念和幂的运算性质的基础上建立起来的函数模型,减轻了学习的难度。从作业情况看,学生的掌握情况得比较好。但是也还存在一些问题,特别是对指数函数的图象和性质的掌握情况还不够好,在后面的学习中应加强。
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
