苏教选修2-1椭圆的标准方程
图片预览



文档简介
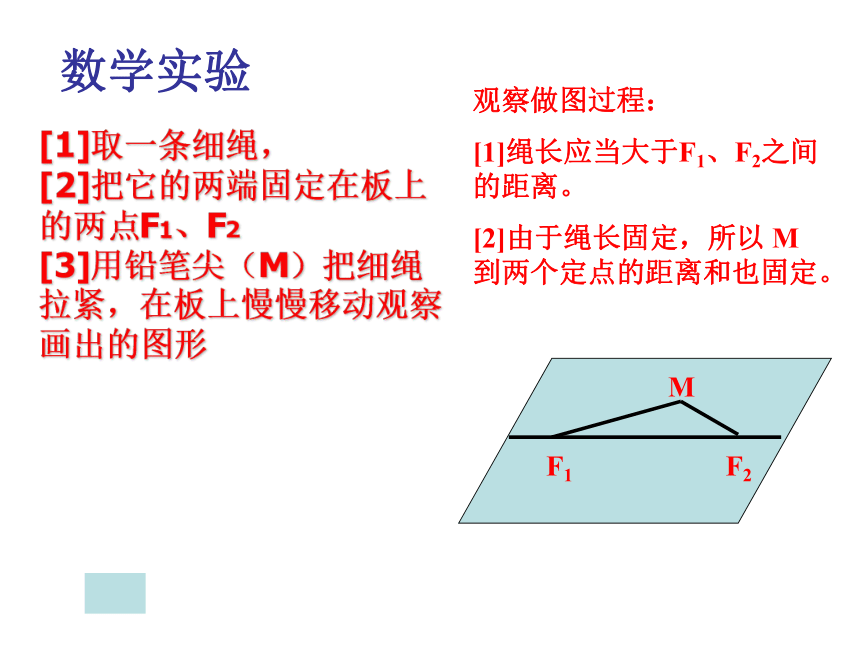
课件17张PPT。F1F2M观察做图过程:
[1]绳长应当大于F1、F2之间的距离。
[2]由于绳长固定,所以 M 到两个定点的距离和也固定。[1]取一条细绳,
[2]把它的两端固定在板上
的两点F1、F2
[3]用铅笔尖(M)把细绳
拉紧,在板上慢慢移动观察
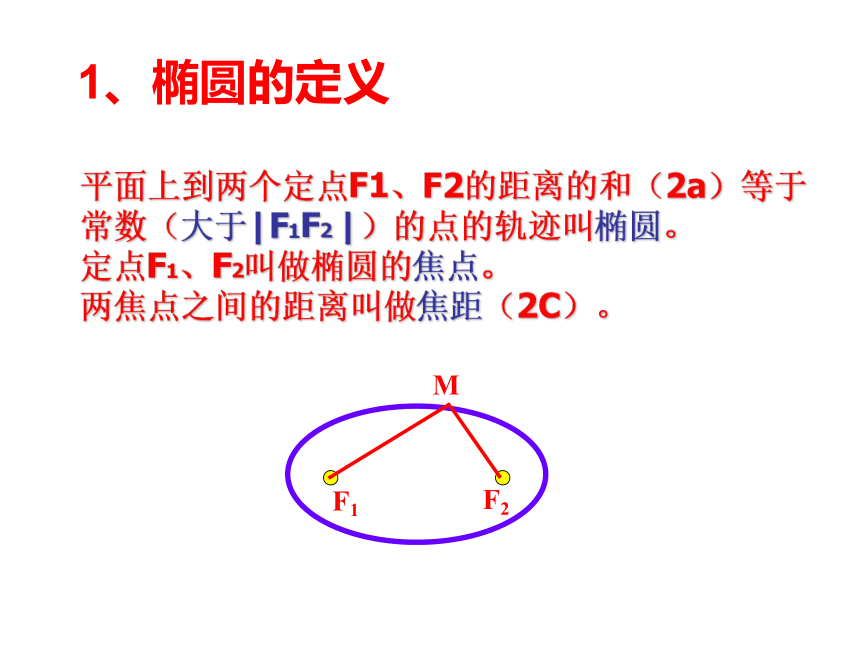
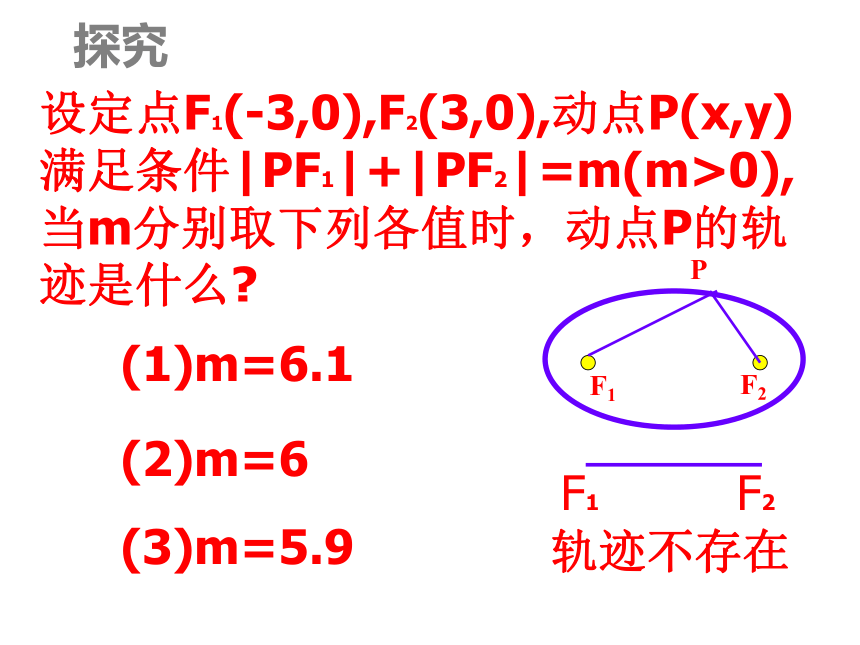
画出的图形数学实验1、椭圆的定义轨迹不存在1、椭圆的定义平面上到两个定点F1、F2的距离的和(2a)等于常数(大于|F1F2 |)的点的轨迹叫椭圆。
定点F1、F2叫做椭圆的焦点。
两焦点之间的距离叫做焦距(2C)。由椭圆的定义2.推导椭圆的标准方程由椭圆的定义知 2a>2c 即 a>c代入上式得化简得方
程
特
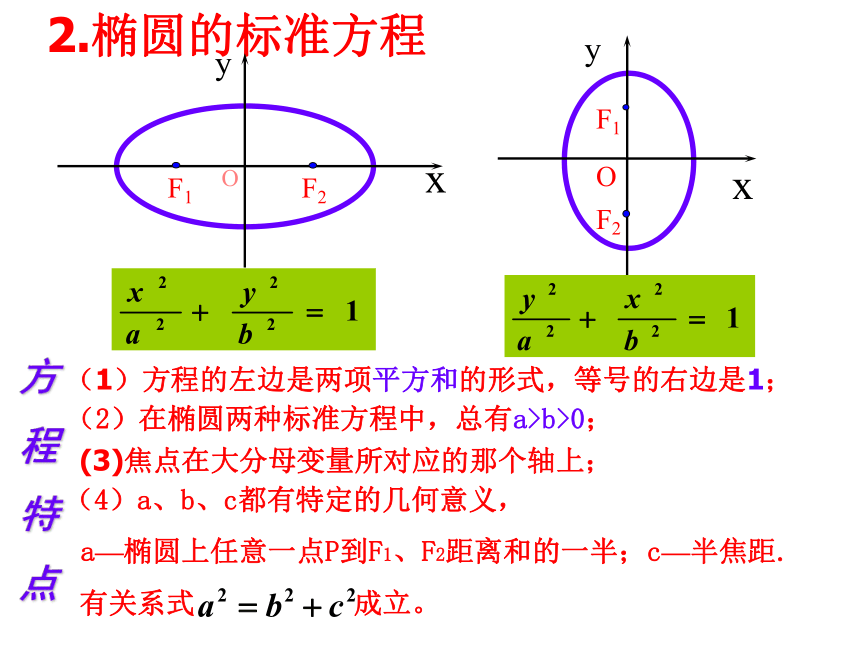
点(2)在椭圆两种标准方程中,总有a>b>0;(4)a、b、c都有特定的几何意义,
a—椭圆上任意一点P到F1、F2距离和的一半;c—半焦距.
有关系式 成立。2.椭圆的标准方程(3)焦点在大分母变量所对应的那个轴上;(1)方程的左边是两项平方和的形式,等号的右边是1;判定下列椭圆的焦点在哪个轴?并指明a2、b2、 c2,写出焦点坐标.答:焦点在 x 轴;(-3,0)和(3,0)答:焦点在 y 轴;(0,-5)和(0,5)答:焦点在y 轴;(0,-1)和(0,1)例题练习答案:C.由椭圆定义:|MF1|+|MF2|=2a=20由方程知 a=10,所以 2a=20,故|MF2|=20-|MF1|=14.总结1.椭圆的定义:平面上到两个定点的距离的和(2a)等于定长(大于|F1F2 |)的点的轨迹叫椭圆。定点F1、F2叫做椭圆的焦点。两焦点之间的距离叫做焦距(2C)。2.椭圆的标准方程3.椭圆方程的求法:直接代入法,待定系数法谢谢实际探究:如图,我国发射的第一颗人造地球卫星的运行轨道,是以地心(地球的中心)F2为一个焦点的椭圆.已知它的近地点A(离地面最近的点)距地面439km,远地点B(离地面最远的点)距地面2384km,并且F2A、B在同一直线上,地球半径约为6371km.
求卫星运行的轨道方程.
解:因为椭圆的焦点在x轴上,所以设它的标准方程为(2)两个焦点坐标分别是(0,-2)和(0,2),且过点(-1.5,2.5).解:因为椭圆的焦点在y轴上,所以设它的标准方程为A答案:A1.将下列方程化为标准方程,并判定焦点在哪个轴上,写出焦点坐标练习
[1]绳长应当大于F1、F2之间的距离。
[2]由于绳长固定,所以 M 到两个定点的距离和也固定。[1]取一条细绳,
[2]把它的两端固定在板上
的两点F1、F2
[3]用铅笔尖(M)把细绳
拉紧,在板上慢慢移动观察
画出的图形数学实验1、椭圆的定义轨迹不存在1、椭圆的定义平面上到两个定点F1、F2的距离的和(2a)等于常数(大于|F1F2 |)的点的轨迹叫椭圆。
定点F1、F2叫做椭圆的焦点。
两焦点之间的距离叫做焦距(2C)。由椭圆的定义2.推导椭圆的标准方程由椭圆的定义知 2a>2c 即 a>c代入上式得化简得方
程
特
点(2)在椭圆两种标准方程中,总有a>b>0;(4)a、b、c都有特定的几何意义,
a—椭圆上任意一点P到F1、F2距离和的一半;c—半焦距.
有关系式 成立。2.椭圆的标准方程(3)焦点在大分母变量所对应的那个轴上;(1)方程的左边是两项平方和的形式,等号的右边是1;判定下列椭圆的焦点在哪个轴?并指明a2、b2、 c2,写出焦点坐标.答:焦点在 x 轴;(-3,0)和(3,0)答:焦点在 y 轴;(0,-5)和(0,5)答:焦点在y 轴;(0,-1)和(0,1)例题练习答案:C.由椭圆定义:|MF1|+|MF2|=2a=20由方程知 a=10,所以 2a=20,故|MF2|=20-|MF1|=14.总结1.椭圆的定义:平面上到两个定点的距离的和(2a)等于定长(大于|F1F2 |)的点的轨迹叫椭圆。定点F1、F2叫做椭圆的焦点。两焦点之间的距离叫做焦距(2C)。2.椭圆的标准方程3.椭圆方程的求法:直接代入法,待定系数法谢谢实际探究:如图,我国发射的第一颗人造地球卫星的运行轨道,是以地心(地球的中心)F2为一个焦点的椭圆.已知它的近地点A(离地面最近的点)距地面439km,远地点B(离地面最远的点)距地面2384km,并且F2A、B在同一直线上,地球半径约为6371km.
求卫星运行的轨道方程.
解:因为椭圆的焦点在x轴上,所以设它的标准方程为(2)两个焦点坐标分别是(0,-2)和(0,2),且过点(-1.5,2.5).解:因为椭圆的焦点在y轴上,所以设它的标准方程为A答案:A1.将下列方程化为标准方程,并判定焦点在哪个轴上,写出焦点坐标练习
