24.2.2直线与圆的位置关系
文档属性
| 名称 | 24.2.2直线与圆的位置关系 |  | |
| 格式 | rar | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-03-18 17:03:00 | ||
图片预览







文档简介
课件22张PPT。课前任务看书P95 --
熟记
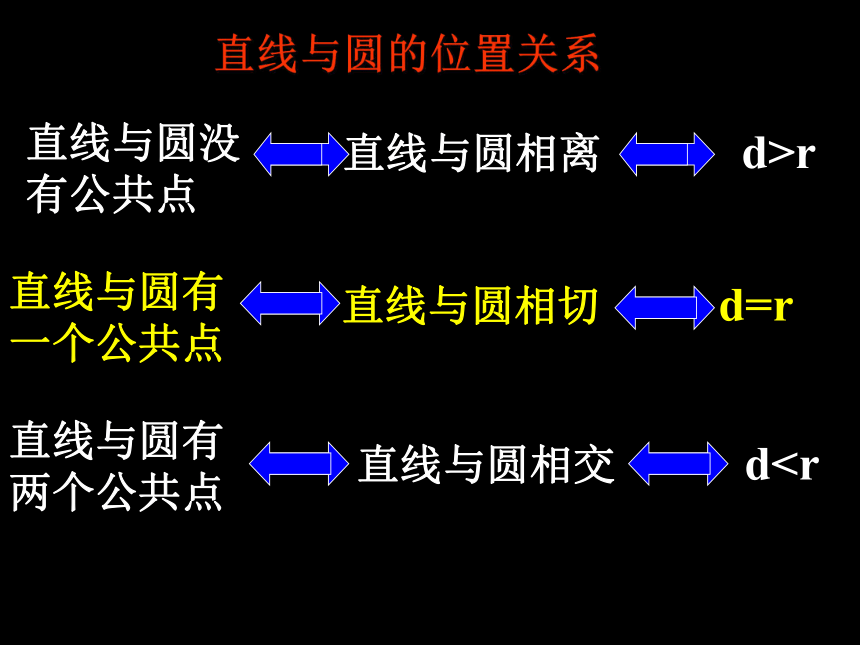
切线的判定定理24.2.2直线与圆的位置关系直线与圆的位置关系 直线与圆相离 d>r直线与圆相交 d 顺着伞的什么方向飞出去的?问题2:砂轮转动时,火花是沿着砂轮的
什么方向飞出去的? 切线的判定定理:
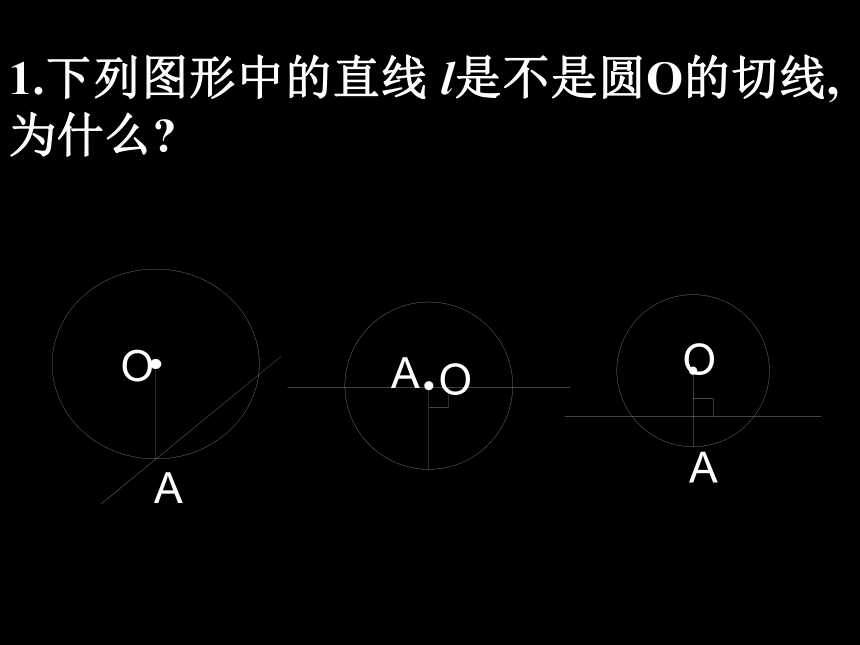
1、切线的判定定理:经过半径外端并且垂直于这条半径的直线是圆的切线.2、对定理的理解:一条直线是圆的切线需满足两条:②垂直于这条半径. 注意:定理中的两个条件缺一不可. ①经过半径外端.1.下列图形中的直线 l是不是圆O的切线,为什么?AAOAOO引例 如图,已知⊙O上一点A ,
过A作⊙O的切线? (1)直线l经过半径OA的外端点A;(2)直线l垂直于半径OA.问题2 观察所作出的切线,
具有两个特征了吗?OAl作法: 1)连结OA.
2)过点A 作OA的垂线l
则直线l就是⊙O的切线2.判断下列命题是否正确.
(1)经过半径外端的直线是圆的切线.( )
(2)垂直于半径的直线是圆的切线.( )
(3)过直径的外端并且垂直于这条直径的直线是圆的切线.( )
(4)和圆有一个公共点的直线是圆的切线.( )
(5)以等腰三角形的顶点为圆心,底边上的高为半径的圆与底边相切.( )
小结 切线的判定方法切线的判定方法有三种:①直线与圆有唯一公共点;②直线到圆心的距离等于该圆的半径;③切线的判定定理. 应用定理.
例1 已知:直线AB经过⊙O上的点C,
并且OA=OB,CA=CB.
求证:直线AB是⊙O的切线. 直线AB经过半径0C的外端C,并且垂直于半径0C, 所以AB是⊙O的切线. ABCO证明:连结0C∵0A=0B,CA=CB,∴0C是等腰三角形0AB底边AB上的中线.∴AB⊥OC.方法小结: 证明过圆上一点的直线是圆的切线.只要证明这条直线垂直于经过切点的半径.例2.如图,线段AB经过圆心O,交⊙O于点A,C,∠BAD=∠B=30°,边BD交圆于点D。
求证:BD是⊙O的切线证明:连结OD∵ OA=OD , ∴ OD⊥BD又∵直线BD 经过⊙O上的D点∴直线BD是⊙O的切线∴∠ODA=∠A=300ABCD∴∠BDO=90°例3.如图,O为∠PAQ的角平分线上的一点,OB⊥AP于点B,以O为圆心OB为半径作⊙B,
求证:AQ与⊙O相切 1.如图, AB是⊙O的直径,∠B=45°,
AC=AB, AC是⊙O的切线吗?
为什么? 随堂练2.如图,在△ABC中 ∠ABC=90°,以AB为直径的⊙O交AC于D,E是BC的中点,连接ED
求证:DE是⊙O的切线随堂练3.如图,已知,AB是⊙O直径,BC⊥AB于B,⊙O的弦AD∥OC,
求证:DC是⊙O的切线.随堂练 4,如图,△ABC为等腰三角形,O为底边BC的中点,OD⊥AB,以O为圆心OD为半径作⊙O,
求证:AC与⊙O相切.随堂练1.如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于D,过点D作DE⊥AC 于点E,交BC的延长线于点F.
.能力与拓展求证:
(1)AD=BD;
(2)DF是⊙O的切线 2.已知:如图, 梯形ABCD中,AD‖BC,∠C=90°,AD+BC=AB,以AB为直径作⊙O.
求证:CD为⊙O的切线.能力与拓展 (2008年烟台市)
如图,AB是⊙O的直径,∠BAC=30°,M是OA上一点,过M作AB的垂线交AC于点N,交BC的延长线于点E,直线CF交EN于点F,且∠ECF=∠E.
(1)证明:CF是⊙O的切线;
(2)设⊙O的半径为1,
且AC=CE,
求MO的长 走进中考 (盐城市2008年)如图,⊙O的半径为3cm,B为⊙O外一点,OB交⊙O于点A,AB=OA,动点P从点A出发,以πcm/s的速度在⊙O上按逆时针方向运动一周回到点A立即停止.当点P运动的时间为 s时,BP与⊙O相切.走进中考1或5P1如何判定一条直线是已知圆的切线?(1)和圆只有一个公共点的直线是圆的切线;(2)和圆心的距离等于半径的直线是圆的切线;(3)过半径外端且和半径垂直的直线
是圆的切线;A , 经过圆上的一点;B, 垂直于半径;
熟记
切线的判定定理24.2.2直线与圆的位置关系直线与圆的位置关系 直线与圆相离 d>r直线与圆相交 d
什么方向飞出去的? 切线的判定定理:
1、切线的判定定理:经过半径外端并且垂直于这条半径的直线是圆的切线.2、对定理的理解:一条直线是圆的切线需满足两条:②垂直于这条半径. 注意:定理中的两个条件缺一不可. ①经过半径外端.1.下列图形中的直线 l是不是圆O的切线,为什么?AAOAOO引例 如图,已知⊙O上一点A ,
过A作⊙O的切线? (1)直线l经过半径OA的外端点A;(2)直线l垂直于半径OA.问题2 观察所作出的切线,
具有两个特征了吗?OAl作法: 1)连结OA.
2)过点A 作OA的垂线l
则直线l就是⊙O的切线2.判断下列命题是否正确.
(1)经过半径外端的直线是圆的切线.( )
(2)垂直于半径的直线是圆的切线.( )
(3)过直径的外端并且垂直于这条直径的直线是圆的切线.( )
(4)和圆有一个公共点的直线是圆的切线.( )
(5)以等腰三角形的顶点为圆心,底边上的高为半径的圆与底边相切.( )
小结 切线的判定方法切线的判定方法有三种:①直线与圆有唯一公共点;②直线到圆心的距离等于该圆的半径;③切线的判定定理. 应用定理.
例1 已知:直线AB经过⊙O上的点C,
并且OA=OB,CA=CB.
求证:直线AB是⊙O的切线. 直线AB经过半径0C的外端C,并且垂直于半径0C, 所以AB是⊙O的切线. ABCO证明:连结0C∵0A=0B,CA=CB,∴0C是等腰三角形0AB底边AB上的中线.∴AB⊥OC.方法小结: 证明过圆上一点的直线是圆的切线.只要证明这条直线垂直于经过切点的半径.例2.如图,线段AB经过圆心O,交⊙O于点A,C,∠BAD=∠B=30°,边BD交圆于点D。
求证:BD是⊙O的切线证明:连结OD∵ OA=OD , ∴ OD⊥BD又∵直线BD 经过⊙O上的D点∴直线BD是⊙O的切线∴∠ODA=∠A=300ABCD∴∠BDO=90°例3.如图,O为∠PAQ的角平分线上的一点,OB⊥AP于点B,以O为圆心OB为半径作⊙B,
求证:AQ与⊙O相切 1.如图, AB是⊙O的直径,∠B=45°,
AC=AB, AC是⊙O的切线吗?
为什么? 随堂练2.如图,在△ABC中 ∠ABC=90°,以AB为直径的⊙O交AC于D,E是BC的中点,连接ED
求证:DE是⊙O的切线随堂练3.如图,已知,AB是⊙O直径,BC⊥AB于B,⊙O的弦AD∥OC,
求证:DC是⊙O的切线.随堂练 4,如图,△ABC为等腰三角形,O为底边BC的中点,OD⊥AB,以O为圆心OD为半径作⊙O,
求证:AC与⊙O相切.随堂练1.如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于D,过点D作DE⊥AC 于点E,交BC的延长线于点F.
.能力与拓展求证:
(1)AD=BD;
(2)DF是⊙O的切线 2.已知:如图, 梯形ABCD中,AD‖BC,∠C=90°,AD+BC=AB,以AB为直径作⊙O.
求证:CD为⊙O的切线.能力与拓展 (2008年烟台市)
如图,AB是⊙O的直径,∠BAC=30°,M是OA上一点,过M作AB的垂线交AC于点N,交BC的延长线于点E,直线CF交EN于点F,且∠ECF=∠E.
(1)证明:CF是⊙O的切线;
(2)设⊙O的半径为1,
且AC=CE,
求MO的长 走进中考 (盐城市2008年)如图,⊙O的半径为3cm,B为⊙O外一点,OB交⊙O于点A,AB=OA,动点P从点A出发,以πcm/s的速度在⊙O上按逆时针方向运动一周回到点A立即停止.当点P运动的时间为 s时,BP与⊙O相切.走进中考1或5P1如何判定一条直线是已知圆的切线?(1)和圆只有一个公共点的直线是圆的切线;(2)和圆心的距离等于半径的直线是圆的切线;(3)过半径外端且和半径垂直的直线
是圆的切线;A , 经过圆上的一点;B, 垂直于半径;
同课章节目录
