8.5怎样判断三角形相似学案3

8.5相似三角形的 判断方法3
山东省单县终兴中学 编写人 王敏 吴新峰 审阅人 吴吉杰
一学习目标：
1掌握三角形相似的判断方法3，并能灵活运用解决问题。
2能综合运用三种判断方法判定两个三角形相似。
二 知识回顾：
1相似三角形的判定方法1：
2相似三角形的判定方法2：
三 自主预习
如果一个三角形的三条边与另一个三角形的三条边 ，那么这两个三角形相似。
四 导学探究：
分别画出△ABC和△DEF，使AB＝3cm，BC＝4.5cm，AC＝6cm，DE＝2cm，EF＝3cm，DF＝4cm.。
（1） 分别计算、、，这三个比值相等吗？
（2） 剪下画出的三角形，利用叠合的方法，检验对应角之间有怎样的大小关系？
（3） △ABC和△DEF相似吗？与他同学交流。
判定方法3：
例3 如图所示，已知＝＝。找出图中相等的角，并说明你的理由 。
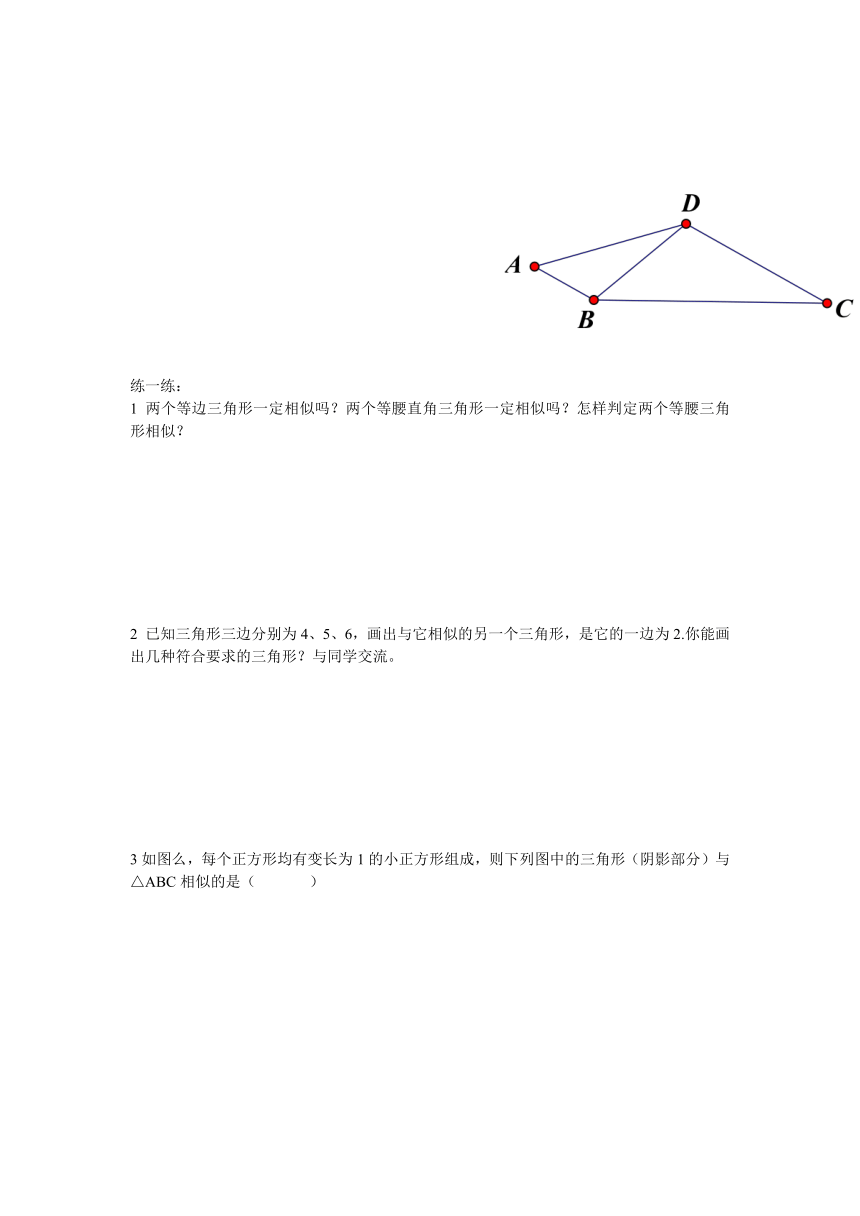
例4 如图所示，某地四个乡镇A、B、C、D之间建有公路，已知AB＝14千米，AD＝28千米，BD＝21千米，BC＝42千米，DC＝31.5千米，公路AB与 DC平行吗？说明你的理由。
练一练：
1 两个等边三角形一定相似吗？两个等腰直角三角形一定相似吗？怎样判定两个等腰三角形相似？
2 已知三角形三边分别为4、5、6，画出与它相似的另一个三角形，是它的一边为2.你能画出几种符合要求的三角形？与同学交流。
3如图么，每个正方形均有变长为1的小正方形组成，则下列图中的三角形（阴影部分）与△ABC相似的是（ ）
A B C
五 当堂达标
1 已知⊿ABC的三边分别为6,7cm.5cm,9cm，⊿DEF的一边长为4 cm，当⊿DEF另两边的长是下列哪一组时，这两个三角形相似（ ）
A 2cm ,3cm B 4cm,5cm C 5cm,6cm D 6cm,7cm
2 如图，在⊿ABC中，点D、E分别在AB、AC边上，DE∥BC,若AD:AB=3:4，AE=6，则AC等于（ ） A 3 B 4 C 6 D 8
（2题） （3题） （4题）
3 如图，四边形ABCD是正方形，点E是CD的中点，点P是边BC上一点，下列条件中，不能推出⊿ABP与⊿ECP相似的是（ ）
A ∠APB=∠EPC B ∠APE=900 C P是BC的中点 D BP:BC=2:3
4 如图，在⊿ABC中，D是AB边上一点，连接CD ，要使⊿ADC与⊿ABC相似，应添加的条件是 （只需要写出一个即可）
5 如图，==,则⊿ABC∽ ，∠BAD=
6 已知，在⊿ABC和⊿A/B/C/中，AB=6cm，BC=8cm，AC=10cm，A/B/=18cm, B/C/=24cm, A/C/=30cm, ⊿ABC和⊿A/B/C/相似吗？说明理由。
六 能力 提升
如图，点O是△ABC外的一点，分别在射线OA,OB,OC上取一点A，，B，，C，，使得＝＝＝3，连接A，B，，B，C，，A，C，，使得△A，B，C，与△ABC是否相似？说明你的结论。
A，
B，
C，