8.5相似三角形的性质学案

8.5相似三角形的性质学案
山东省单县终兴中学 编写人 王敏 吴新峰 审阅人吴吉杰
一学习目标：
1掌握相似三角形的性质。
2能够灵活运用相似三角形的性质解决实际问题。
二 知识回顾：
相似三角形的判断方法：
1
2
3 。
三自主预习：
1 两个相似三角形对应高的比等于它们 的比。
2两个相似三角形面积的比等于它们 比的 。
想一想：
相似三角形对应边上的中线的比、相似三角形对应角平分线的比、相似三角形周长的比都等于对应边的比吗？
四导学探究：
探究1
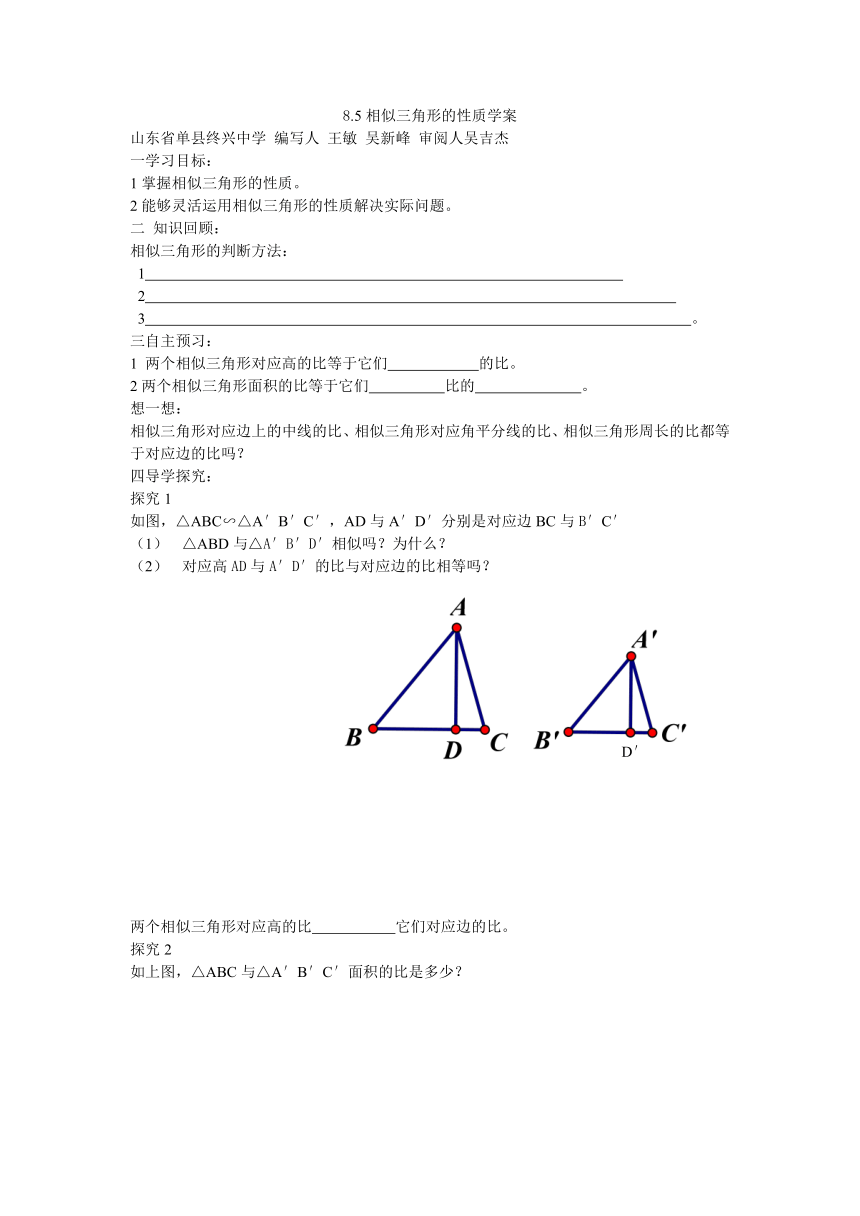
如图，△ABC∽△A′B′C′，AD与A′D′分别是对应边BC与B′C′
（1） △ABD与△A′B′D′相似吗？为什么？
（2） 对应高AD与A′D′的比与对应边的比相等吗？
两个相似三角形对应高的比 它们对应边的比。
探究2
如上图，△ABC与△A′B′C′面积的比是多少？
两个相似三角形的面积的比等于 。
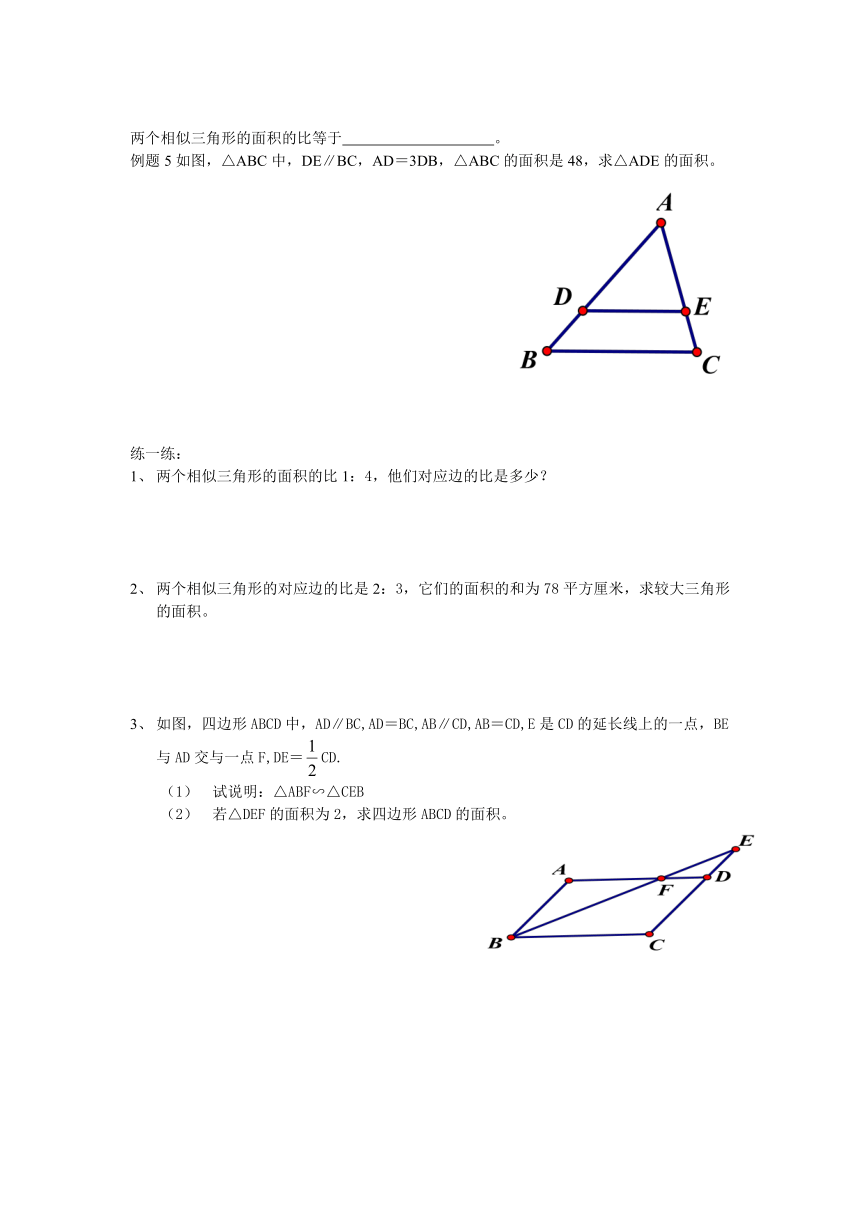
例题5如图，△ABC中，DE∥BC，AD＝3DB，△ABC的面积是48，求△ADE的面积。
练一练：
1、 两个相似三角形的面积的比1：4，他们对应边的比是多少？
2、 两个相似三角形的对应边的比是2：3，它们的面积的和为78平方厘米，求较大三角形的面积。
3、 如图，四边形ABCD中，AD∥BC,AD＝BC,AB∥CD,AB＝CD,E是CD的延长线上的一点，BE与AD交与一点F,DE＝CD.
（1） 试说明：△ABF∽△CEB
（2） 若△DEF的面积为2，求四边形ABCD的面积。
五 当堂达标：
1、如图1，小明在A时测得某树的影长为2m,B时又测得该树的影长为8m,若两次日照的光线互相垂直，则数的高度为 m.
(1) (2)
2、如图2，上体育课时，甲和乙两名同学分别站在C、D的位置时，乙的影子恰好在甲的影子里边，已知甲乙两名同学相距1米，甲的身高为1.8米，乙的身高为1.5米，则甲的影长为 米。
3、如图3，A、B两点被池塘隔开，在AB外取一点C，连接AC、BC，在AC上取一点M,使AM＝3MC，作MN∥AB,交BC于N,量得MN＝38m，则AB的长为 。
4、如图4，把△ABC平移到△A,B,C,的位置，它们重合部分（即图中的阴影部分）的面积是△ABC的一半，若AB＝，则此三角形移动的距离A A,是 。
（3） （4）
5、在△ABC和△DEF中，AB＝2DE,AC＝2DF,∠D＝∠A,如果△ABC的周长是16，面积是12，那么△DEF的周长和面积依次为（ ）
A8,3 B8,6 C4,3 D4,6
6、如图某校数学兴趣小组为测量学校旗杆AC的高度，在点F处竖立一根长为1.5米的标杆DF,如图（5）所示，量出DF 的影子EF的长度为1米，在量出旗杆AC的影长BC的长度为6米，那么旗杆AC的高度为（ ）
A6米 B7米 C8.5米 D9米
(5) (6)
7、如图（6）所示，在△ABC中，D,E分别是边AC,AB的中点，连接BD,若BD平分
∠ABC,则下列结论中错误的是（ ）
ABC=2BE B∠A=∠EDA CBC=2AD DBD⊥AC
六 能力提升：
1一块直角三角形的木板的一条直角边AB的长为1.5米，面积为1.5平方米，要把它加工成面积尽可能大的方桌面，甲、乙两位同学的方法如图（1）（2）所示。请你用学过的方法说明哪位同学的加工方法更好（加工损耗忽略不计，计算结果的分数可保留）
D′