新人教七上一元一次方程应用复习
文档属性
| 名称 | 新人教七上一元一次方程应用复习 |

|
|
| 格式 | rar | ||
| 文件大小 | 148.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-03-18 00:00:00 | ||
图片预览










文档简介
课件41张PPT。一元一次方程应用题复习沿中 马晓斌应用题的解法很多,以下几种:
1)列表法
2)图示法
3)演示法
4)实践法设未知数的技巧:1、设直接未知数,即求什么设什么。2、设间接未知数。3、设辅助未知数,即“设而不求”在列方程解决实际问题的过程应
注意哪些问题?
(1)设未知数时,要仔细分析问题中的数量关系,
找出题中的已知条件和未知数,一般采用直接
设法,有些问题可用间接设法,要注意未知数
的单位,不要漏写。
(2)找等量关系时,可借助图表分析题中的数
量关系, 列出两个代数式,使它们都表示
一个相等或相同的量。
(3)列方程时,要注意方程各项是同类量,
单位要一致,方程左右两边应是等量。
(4)解出方程的解后,要验证它的合理性,
再解释它的意义,并要注意单位。
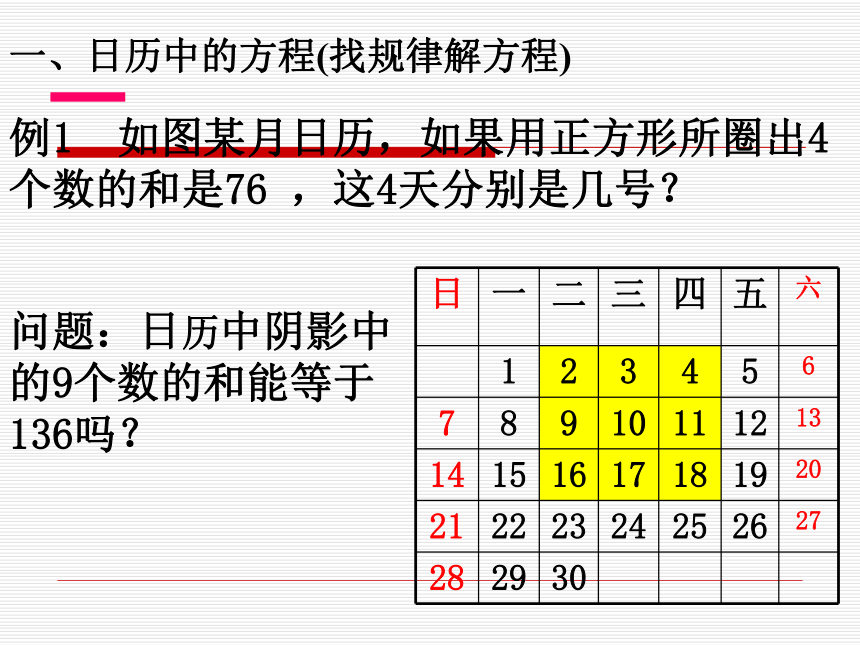
一、日历中的方程(找规律解方程)例1 如图某月日历,如果用正方形所圈出4个数的和是76 ,这4天分别是几号?问题:日历中阴影中的9个数的和能等于136吗? 如下图,将一张正方形纸片,剪成四个大小形状一样的小正方形,然后
将其中的一个小正方形再按同样的方法剪成四个小正方形,再将其中的一个
小正方形剪成四个小正方形,如此循环进行下去;
(1)填表:
?
?
?
?
?
?
?
(2)如果剪n次,共剪出多少个小正方形?
(3)如果共剪出301个小正方形,则剪了几 次?
4 7 10 13 16有一些分别标有6,12,18,24,30,36,…..的卡片,小明从中任意拿到了相邻的3张卡片,发现这些卡片上的数字的和为342
猜猜小明拿到了哪3张卡片?
小明能否拿到相邻的3张卡片,使得它们的和为86?说明理由?(2)周长为一定时,当长和宽相等时面积最大。例题:用一根长为10米的铁丝围成一个长方形,
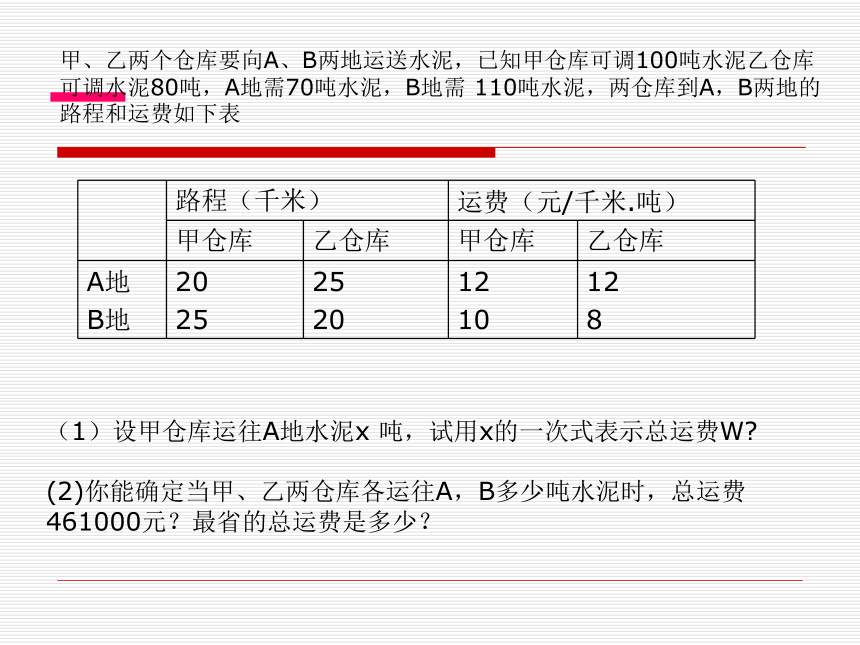
(1)使得长方形的长比宽多1.4米,此时长方形的长、宽各为多少米?(2)使得长方形的长比宽多0.8米,此时长方形的长、宽各为多少米?它所围成的长方形与(1)中所围长方形相比,面积有什么变化? 例1:甲仓库有存粮120吨,乙仓库有存粮食80吨,现从甲库调部分到乙库,若要求调运后甲库的存粮是乙库的 ,问应从甲库调多少吨粮食到乙库?例2:某公司原有职员60名,其中女职员占20%,今年又有几位男职员辞职,公司又补招了3名女职员,女职员的比例提高到25%,问公司离开公司的男职员一共有几人?甲、乙两个仓库要向A、B两地运送水泥,已知甲仓库可调100吨水泥乙仓库可调水泥80吨,A地需70吨水泥,B地需 110吨水泥,两仓库到A,B两地的路程和运费如下表(1)设甲仓库运往A地水泥x 吨,试用x的一次式表示总运费W? (2)你能确定当甲、乙两仓库各运往A,B多少吨水泥时,总运费461000元?最省的总运费是多少?例 我国四大发明之一的黑火药是用硝酸钠、
硫磺、木炭三种,原料按15:2:3的比例
配制而成,现要配制这种火药150公斤,
则这三种原料各需要多少 公斤?解:设需要硝酸钠15x公斤,硫磺2x公斤,
木炭3x公斤依题意得:15x+2x+3x=150
x=7.515x=15×7.5=112.5 2x=2×7.5=15
3x=3×7.5=22.5
答:硝酸钠应取112.5公斤,硫磺取15公斤,木炭
应取 22.5公斤。按比例分配应用题设元是间接设元,一般设其中的一份为x,
必要时要求连比相等关系一般是总量等于部分量的和或
找题中的话,也可以是整个题中始终不变的量 ?按比例分配的应用题的设元和找相等关系
各有什么特点?一、明确行程问题中三个量的关系三个基本量关系是:速度×时间=路程分析方法辅助手段:线型图示法分析方法辅助手段:线型图示法相遇问题:甲的路程+乙的路程=全程追及问题:(1)同地不同时:慢者行程+先行路程=快者路程(2)同时不同地:快者路程 — 慢者行程=间隔距离行程问题1、甲、乙两地相距162公里,一列慢车从甲站开出,每小时走48公里,一列快车从乙站开出,每小时走60公里试问: 1)两列火车同时相向而行,多少时间可以相遇?
2)两车同时反向而行,几小时后两车相距270公里?3)若两车相向而行,慢车先开出1小时,再用多少时间
两车才能相遇?4)若两车相向而行,快车先开25分钟,快车开了几小时
与慢车相遇?
5)两车同时同向而行(快车在后面),几小时后快车
可以追上慢车?6)两车同时同向而行(慢车在后面),几小时后两车相
距200公里? 2:从甲地到乙地,水路比公路近40千米,上午十时,一艘轮船从甲地驶往乙地,下午1时一辆汽车从甲地驶往乙地,结果同时到达终点。已知轮船的速度是每小时24千米,汽车的速度是每小时40千米,求甲、乙两地水路、公路的长,以及汽车和轮船行驶的时间?解:设水路长为x千米,则公路长为(x+40)千米等量关系:船行时间-车行时间=3小时答:水路长240千米,公路长为280千米,车行时间为
7小时,船行时间为10小时 依题意得:
x+40=280,x=2403、 某连队从驻地出发前往某地执行任务,行军速度是
6千米/小时,18分钟后,驻地接到紧急命令,派遣
通讯员小王必须在一刻钟内把命令传达到该连队,
小王骑自行车以14千米/小时的速度沿同一路线追赶
连队,问是否能在规定时间内完成任务?
等量关系:小王所行路程=连队所行路程答:小王能在指定时间内完成任务。解:设小王追上连队需要x小时,则小王行驶的路程为
14x千米,连队所行路程是 千米依题意得:4 一列客车和一列货车在平行的轨道上同向行驶,
客车的长是200米,货车的长是280米,客车的
速度与货车的速度比是5 :3,客车赶上货车的
交叉时间是1分钟,求各车的速度;若两车相向
行驶,它们的交叉时间是多少分钟?
解:设客车的速度是5x米/分,
则货车的速度是3x米/分。
依题意得:5x – 3x = 280 + 200x=2405x = 1200,3x = 720设两车相向行驶的交叉时间为y分钟。依题意得:1200y+720y= 280 + 200y=0.255:一架飞机飞行两城之间,顺风时需要5小时30分钟,
逆风时需要6小时,已知风速为每小时24公里,
求两城之间的距离?
等量关系:顺风时飞机行驶的路程=逆风时飞机行驶的路程。答:两城之间的距离为3168公里注:飞行问题也是行程问题。同水流问题一样,飞行问
题的等量关系有:顺风飞行速度=飞机本身速度+风速
逆风飞行速度=飞机本身速度-风速5.5(x+24)=6(x-24)
解得:x=552解:静风的速度为x公里/小时,由题意得:
∴6(x-24)=3168练习1、甲、乙两人环绕周长是400米的跑道散步,如果两人从 同一地点背道而行,那么经过2分钟他们两人就要相遇。如果2人从同一地点同向而行,那么经过20分钟两人相 遇。如果甲的速度比乙的速度快,求两人散步的速度?
等量关系:甲行的路程-乙行的路程=环形周长注:同时同向出发:
快车走的路程-环行跑道周长=慢车走的路程(第一次相遇)
同时反向出发:
甲走的路程+乙走的路程=环行周长(第一次相遇)
练习2、甲乙两人从同一村庄步行去县城,甲比乙早1小时出发,而晚1小时到达,甲每小时走4千米,乙每小时走6千米,求村庄到县城的距离?3、两地相距28公里,小明以15公里/小时的速度。小亮以
30公里/小时的速度,分别骑自行车和开汽车从同一地
前往另一地,小明先出发1小时,小亮几小时后才能
追上小明?解:设小亮开车x 小时后才能追上小明,则小亮所行路
程为30x公里,小明所行路程为15(x+1)
等量关系:小亮所走路程=小明所走路程
依题意得:30x=15(x+1)
x=1检验:两地相距28公里,在两地之间,小亮追不上小明1) 工作效率=2)工作总量=工作效率×工作时间3)工作时间=4)各队合作工作效率=各队工作效率之和5)全部工作量之和=各队工作量之和工程问题中的数量关系例1 修筑一条公路,甲工程队单独承包要80天完成,乙工程队单独
承包要120天完成
1)现在由两个工程队合作承包,几天可以完成?
2)如果甲、乙两工程队合作了30天后,因甲工作队另有任务,
剩下工作由乙工作队完成,则修好这条公路共需要几天?
解: 1)设两工程队合作需要x天完成。
2)设修好这条公路共需要 y 天完成。
等量关系: 甲30天工作量+乙队y天的工作量 = 1
答:两工程队合作需要48天完成,修好这条公路还需75天。等量关系:甲工作量+乙工作量=1
依题意得
依题意得y=75x=48例2 已知开管注水缸,10分钟可满,拨开底塞,满缸水20
分钟流完,现若管、塞同开,若干时间后,将底塞塞
住,又过了2倍的时间才注满水缸,求管塞同开的时
间是几分钟?分析:设两管同开x分钟
等量关系:注入量-放出量=缸的容量
依题意得: x=4
答:管塞同开的时间为4分钟x+2x=3x(分钟)x(分钟)解:设再经过x小时水槽里的水恰好等于水槽的等量关系:甲管流进水的水+乙管流出的水 =水槽的 依题意得:
答:再经过 小时水槽里的水恰好是水槽容量的例6 一个水池装甲、乙、丙三根水管,单开甲管10小时
可注满水池,单开乙管15小时可注满,单开丙管20
小时可注满。现在三管齐开,中途甲管关闭,结果6
小时把水池注满,问甲管实际开了几个小时?
解:设甲管实际开了x小时
等量关系:甲管x小时的工作量+乙、丙两管同开
6 小时的工作量)= 1
答:甲管实际开了3小时。
依题意得:
x=3等量关系:4天的工作量+改进后(x – 4)工作量= 0.5解:设一共x天可以修完它的一半。
依题意得 ×4+ (x—4)= 0.5
答:一共 天可以修完它的一半。例7分析:x=例题举例
一个三位数,它的百位上的数比十位上的数的2倍 大1,个位上的数比十位上的数的3倍小1,如果把这个三位数的百位上的数字和个位上的数字对调,
那么得到的三位数比原来的三位数大99, 求原来的三位数。解:设十位上的数字为x,则百位上的数字为2x+1
个位上的数字为3x -1等量关系:新三位数-原三位数=99依题意,得:[100(3x -1)+10x+(2x+1)] -
[100(2x+1)+10x+(3x -1)] =99
x=3
2x+1=7 3x-1=8答:原来这个三位数为738。数字应用题练习
1) 一个三位数,三个数位上的数字之和是15,个位上
的数是十位上的数的3倍,百位上的数比十位上的
数多5,求这个三位数。 解:设十位上的数字为x,则个位上的数字为3x,百
位上的数字为x+5。等量关系:个位数字+十位数字+百位数字=15依题意,得:3x+ x +x +5 =15
x=2
3x=6 x+5=7 答:这个三位数是726已知四位数 ab52 的三倍比四位数52ab 大39,
求四位数ab52 ?——————等量关系:原数的3倍=新数+39依题意,得:3(100x+52)=(5200+x)+39
x=17七、百分率应用题利润= 售价-进价 售价=标价×折数/10
利润率=利润/进价例题1:一商店把货品按标价的九折出售,仍可获利12.5 %,若货品近价为380元,则标价为多少元?例题2:一商店经销一种商品,由于进货价格降低了6.4 %,使得利润率提高了8个百分点,求原来经销这种商品的利润率.百分率应用题 小颖的服装店同时卖出两套服装,每套均为168元,按成本计算,其中一套盈利20%,另一套亏本20%,请你帮小颖算算,在这次买卖中是亏了还是赚了,还是不亏不赚?例2 小明的爸爸前年存了年利率为2.43%的两年期
定期储蓄。今年到期后,扣除利息税20%,
所得利息正好为小明买了一个价值48.6元的
计算器,问小明爸爸前年存了多少钱?解:设小明爸爸前年存了x元。依题意得:2 × 2.43%x (1- 20%)= 48.6
解之,得 x = 1250
答:小明爸爸前年存了1250元钱等量关系:利息-利息税=应得利息利息 = 本金 × 年利率 × 期数利息税 = 本金 × 年利率 × 期数×税率(20%)存款利息应用题某工厂食堂第三季度一共节煤7400斤,其中八
月份比七月份多节约20%,九月份比八月份多
节约25%,问该厂食堂九月份节约煤多少公斤?依题意得:x+ (1+20%)x +(1+20%)(1+25%)x=7400
解之,得 答:该食堂九月份节约煤3000公斤.(间接设元)
解:设七月份节约煤x公斤。
则八月份节约煤(1+20%)x 公斤,
九月份节约煤(1+20%)(1+25%)x公斤x=2000(1+20%) (1+25%)x=3000增长率应用题练习1 学校准备添置一批课桌椅,原订购60套,每套 100元。店方表示:如果多购可以优惠,结果
校方购了72套,每套减价3元,但商店获得同样
多的利润,求每套课桌椅的成本是多少?(直接设元)
解:设每套课桌椅的成本价为x 元。
依题意得: 60(100 - x)= 72(100 – 3 – x)
解之,得 x = 82答:每套课桌椅的成本是82元。等量关系:60套时总利润=72套时总利润练习2、某商店经销一种商品,由于进货价降低了5%,售出价 不变,使得利润率有原来的m%提高到(m + 6)%, 求m的值。分析: 等量关系是售出价不变,两种不同利润率下的售价各如何表示?成本我们可以设为“1”
解: (1 + m%)=(1 – 5%)[ 1 +(m + 6)% ]解之,得 m = 14练习3:小颖的父母存三年期教育储蓄,三年后取出了5000元钱,你能求出本金是多少吗?有理数应用题举例 例2 你喜欢吃拉面吗?拉面馆的师傅,用一根很粗的面条,
把两头捏合在一起拉伸,再捏合,再拉伸,反复几次,就
把这根很粗的面条拉成了许多细的面条,如下图所示:
第一次捏合 第二次捏合 第三次捏合(1)这样捏合4次后可拉出多少根面条?5次呢?n次呢?
(2)捏合多少次后可拉出64根面条?3 6 9 12这时s又分别是多少呢? 黑蚂蚁和红蚂蚁都认为自己跑得比对方快,刚好它们看到地上的几个半圆(图1),于是它们决定比一比。黑蚂蚁沿着大半圆从甲处跑到乙处;红蚂蚁沿着两个小半圆也从甲处跑到乙处。两只蚂蚁同时起跑,
(1)?? 两只蚂蚁请你帮助判断:谁跑得快?
?(2)两只蚂蚁对你的判断结果很不满意,决定再到(图2)的几个半圆处再比赛一次,请你猜一猜,哪一只蚂蚁先从甲处跑到乙处?
?
思考
1)列表法
2)图示法
3)演示法
4)实践法设未知数的技巧:1、设直接未知数,即求什么设什么。2、设间接未知数。3、设辅助未知数,即“设而不求”在列方程解决实际问题的过程应
注意哪些问题?
(1)设未知数时,要仔细分析问题中的数量关系,
找出题中的已知条件和未知数,一般采用直接
设法,有些问题可用间接设法,要注意未知数
的单位,不要漏写。
(2)找等量关系时,可借助图表分析题中的数
量关系, 列出两个代数式,使它们都表示
一个相等或相同的量。
(3)列方程时,要注意方程各项是同类量,
单位要一致,方程左右两边应是等量。
(4)解出方程的解后,要验证它的合理性,
再解释它的意义,并要注意单位。
一、日历中的方程(找规律解方程)例1 如图某月日历,如果用正方形所圈出4个数的和是76 ,这4天分别是几号?问题:日历中阴影中的9个数的和能等于136吗? 如下图,将一张正方形纸片,剪成四个大小形状一样的小正方形,然后
将其中的一个小正方形再按同样的方法剪成四个小正方形,再将其中的一个
小正方形剪成四个小正方形,如此循环进行下去;
(1)填表:
?
?
?
?
?
?
?
(2)如果剪n次,共剪出多少个小正方形?
(3)如果共剪出301个小正方形,则剪了几 次?
4 7 10 13 16有一些分别标有6,12,18,24,30,36,…..的卡片,小明从中任意拿到了相邻的3张卡片,发现这些卡片上的数字的和为342
猜猜小明拿到了哪3张卡片?
小明能否拿到相邻的3张卡片,使得它们的和为86?说明理由?(2)周长为一定时,当长和宽相等时面积最大。例题:用一根长为10米的铁丝围成一个长方形,
(1)使得长方形的长比宽多1.4米,此时长方形的长、宽各为多少米?(2)使得长方形的长比宽多0.8米,此时长方形的长、宽各为多少米?它所围成的长方形与(1)中所围长方形相比,面积有什么变化? 例1:甲仓库有存粮120吨,乙仓库有存粮食80吨,现从甲库调部分到乙库,若要求调运后甲库的存粮是乙库的 ,问应从甲库调多少吨粮食到乙库?例2:某公司原有职员60名,其中女职员占20%,今年又有几位男职员辞职,公司又补招了3名女职员,女职员的比例提高到25%,问公司离开公司的男职员一共有几人?甲、乙两个仓库要向A、B两地运送水泥,已知甲仓库可调100吨水泥乙仓库可调水泥80吨,A地需70吨水泥,B地需 110吨水泥,两仓库到A,B两地的路程和运费如下表(1)设甲仓库运往A地水泥x 吨,试用x的一次式表示总运费W? (2)你能确定当甲、乙两仓库各运往A,B多少吨水泥时,总运费461000元?最省的总运费是多少?例 我国四大发明之一的黑火药是用硝酸钠、
硫磺、木炭三种,原料按15:2:3的比例
配制而成,现要配制这种火药150公斤,
则这三种原料各需要多少 公斤?解:设需要硝酸钠15x公斤,硫磺2x公斤,
木炭3x公斤依题意得:15x+2x+3x=150
x=7.515x=15×7.5=112.5 2x=2×7.5=15
3x=3×7.5=22.5
答:硝酸钠应取112.5公斤,硫磺取15公斤,木炭
应取 22.5公斤。按比例分配应用题设元是间接设元,一般设其中的一份为x,
必要时要求连比相等关系一般是总量等于部分量的和或
找题中的话,也可以是整个题中始终不变的量 ?按比例分配的应用题的设元和找相等关系
各有什么特点?一、明确行程问题中三个量的关系三个基本量关系是:速度×时间=路程分析方法辅助手段:线型图示法分析方法辅助手段:线型图示法相遇问题:甲的路程+乙的路程=全程追及问题:(1)同地不同时:慢者行程+先行路程=快者路程(2)同时不同地:快者路程 — 慢者行程=间隔距离行程问题1、甲、乙两地相距162公里,一列慢车从甲站开出,每小时走48公里,一列快车从乙站开出,每小时走60公里试问: 1)两列火车同时相向而行,多少时间可以相遇?
2)两车同时反向而行,几小时后两车相距270公里?3)若两车相向而行,慢车先开出1小时,再用多少时间
两车才能相遇?4)若两车相向而行,快车先开25分钟,快车开了几小时
与慢车相遇?
5)两车同时同向而行(快车在后面),几小时后快车
可以追上慢车?6)两车同时同向而行(慢车在后面),几小时后两车相
距200公里? 2:从甲地到乙地,水路比公路近40千米,上午十时,一艘轮船从甲地驶往乙地,下午1时一辆汽车从甲地驶往乙地,结果同时到达终点。已知轮船的速度是每小时24千米,汽车的速度是每小时40千米,求甲、乙两地水路、公路的长,以及汽车和轮船行驶的时间?解:设水路长为x千米,则公路长为(x+40)千米等量关系:船行时间-车行时间=3小时答:水路长240千米,公路长为280千米,车行时间为
7小时,船行时间为10小时 依题意得:
x+40=280,x=2403、 某连队从驻地出发前往某地执行任务,行军速度是
6千米/小时,18分钟后,驻地接到紧急命令,派遣
通讯员小王必须在一刻钟内把命令传达到该连队,
小王骑自行车以14千米/小时的速度沿同一路线追赶
连队,问是否能在规定时间内完成任务?
等量关系:小王所行路程=连队所行路程答:小王能在指定时间内完成任务。解:设小王追上连队需要x小时,则小王行驶的路程为
14x千米,连队所行路程是 千米依题意得:4 一列客车和一列货车在平行的轨道上同向行驶,
客车的长是200米,货车的长是280米,客车的
速度与货车的速度比是5 :3,客车赶上货车的
交叉时间是1分钟,求各车的速度;若两车相向
行驶,它们的交叉时间是多少分钟?
解:设客车的速度是5x米/分,
则货车的速度是3x米/分。
依题意得:5x – 3x = 280 + 200x=2405x = 1200,3x = 720设两车相向行驶的交叉时间为y分钟。依题意得:1200y+720y= 280 + 200y=0.255:一架飞机飞行两城之间,顺风时需要5小时30分钟,
逆风时需要6小时,已知风速为每小时24公里,
求两城之间的距离?
等量关系:顺风时飞机行驶的路程=逆风时飞机行驶的路程。答:两城之间的距离为3168公里注:飞行问题也是行程问题。同水流问题一样,飞行问
题的等量关系有:顺风飞行速度=飞机本身速度+风速
逆风飞行速度=飞机本身速度-风速5.5(x+24)=6(x-24)
解得:x=552解:静风的速度为x公里/小时,由题意得:
∴6(x-24)=3168练习1、甲、乙两人环绕周长是400米的跑道散步,如果两人从 同一地点背道而行,那么经过2分钟他们两人就要相遇。如果2人从同一地点同向而行,那么经过20分钟两人相 遇。如果甲的速度比乙的速度快,求两人散步的速度?
等量关系:甲行的路程-乙行的路程=环形周长注:同时同向出发:
快车走的路程-环行跑道周长=慢车走的路程(第一次相遇)
同时反向出发:
甲走的路程+乙走的路程=环行周长(第一次相遇)
练习2、甲乙两人从同一村庄步行去县城,甲比乙早1小时出发,而晚1小时到达,甲每小时走4千米,乙每小时走6千米,求村庄到县城的距离?3、两地相距28公里,小明以15公里/小时的速度。小亮以
30公里/小时的速度,分别骑自行车和开汽车从同一地
前往另一地,小明先出发1小时,小亮几小时后才能
追上小明?解:设小亮开车x 小时后才能追上小明,则小亮所行路
程为30x公里,小明所行路程为15(x+1)
等量关系:小亮所走路程=小明所走路程
依题意得:30x=15(x+1)
x=1检验:两地相距28公里,在两地之间,小亮追不上小明1) 工作效率=2)工作总量=工作效率×工作时间3)工作时间=4)各队合作工作效率=各队工作效率之和5)全部工作量之和=各队工作量之和工程问题中的数量关系例1 修筑一条公路,甲工程队单独承包要80天完成,乙工程队单独
承包要120天完成
1)现在由两个工程队合作承包,几天可以完成?
2)如果甲、乙两工程队合作了30天后,因甲工作队另有任务,
剩下工作由乙工作队完成,则修好这条公路共需要几天?
解: 1)设两工程队合作需要x天完成。
2)设修好这条公路共需要 y 天完成。
等量关系: 甲30天工作量+乙队y天的工作量 = 1
答:两工程队合作需要48天完成,修好这条公路还需75天。等量关系:甲工作量+乙工作量=1
依题意得
依题意得y=75x=48例2 已知开管注水缸,10分钟可满,拨开底塞,满缸水20
分钟流完,现若管、塞同开,若干时间后,将底塞塞
住,又过了2倍的时间才注满水缸,求管塞同开的时
间是几分钟?分析:设两管同开x分钟
等量关系:注入量-放出量=缸的容量
依题意得: x=4
答:管塞同开的时间为4分钟x+2x=3x(分钟)x(分钟)解:设再经过x小时水槽里的水恰好等于水槽的等量关系:甲管流进水的水+乙管流出的水 =水槽的 依题意得:
答:再经过 小时水槽里的水恰好是水槽容量的例6 一个水池装甲、乙、丙三根水管,单开甲管10小时
可注满水池,单开乙管15小时可注满,单开丙管20
小时可注满。现在三管齐开,中途甲管关闭,结果6
小时把水池注满,问甲管实际开了几个小时?
解:设甲管实际开了x小时
等量关系:甲管x小时的工作量+乙、丙两管同开
6 小时的工作量)= 1
答:甲管实际开了3小时。
依题意得:
x=3等量关系:4天的工作量+改进后(x – 4)工作量= 0.5解:设一共x天可以修完它的一半。
依题意得 ×4+ (x—4)= 0.5
答:一共 天可以修完它的一半。例7分析:x=例题举例
一个三位数,它的百位上的数比十位上的数的2倍 大1,个位上的数比十位上的数的3倍小1,如果把这个三位数的百位上的数字和个位上的数字对调,
那么得到的三位数比原来的三位数大99, 求原来的三位数。解:设十位上的数字为x,则百位上的数字为2x+1
个位上的数字为3x -1等量关系:新三位数-原三位数=99依题意,得:[100(3x -1)+10x+(2x+1)] -
[100(2x+1)+10x+(3x -1)] =99
x=3
2x+1=7 3x-1=8答:原来这个三位数为738。数字应用题练习
1) 一个三位数,三个数位上的数字之和是15,个位上
的数是十位上的数的3倍,百位上的数比十位上的
数多5,求这个三位数。 解:设十位上的数字为x,则个位上的数字为3x,百
位上的数字为x+5。等量关系:个位数字+十位数字+百位数字=15依题意,得:3x+ x +x +5 =15
x=2
3x=6 x+5=7 答:这个三位数是726已知四位数 ab52 的三倍比四位数52ab 大39,
求四位数ab52 ?——————等量关系:原数的3倍=新数+39依题意,得:3(100x+52)=(5200+x)+39
x=17七、百分率应用题利润= 售价-进价 售价=标价×折数/10
利润率=利润/进价例题1:一商店把货品按标价的九折出售,仍可获利12.5 %,若货品近价为380元,则标价为多少元?例题2:一商店经销一种商品,由于进货价格降低了6.4 %,使得利润率提高了8个百分点,求原来经销这种商品的利润率.百分率应用题 小颖的服装店同时卖出两套服装,每套均为168元,按成本计算,其中一套盈利20%,另一套亏本20%,请你帮小颖算算,在这次买卖中是亏了还是赚了,还是不亏不赚?例2 小明的爸爸前年存了年利率为2.43%的两年期
定期储蓄。今年到期后,扣除利息税20%,
所得利息正好为小明买了一个价值48.6元的
计算器,问小明爸爸前年存了多少钱?解:设小明爸爸前年存了x元。依题意得:2 × 2.43%x (1- 20%)= 48.6
解之,得 x = 1250
答:小明爸爸前年存了1250元钱等量关系:利息-利息税=应得利息利息 = 本金 × 年利率 × 期数利息税 = 本金 × 年利率 × 期数×税率(20%)存款利息应用题某工厂食堂第三季度一共节煤7400斤,其中八
月份比七月份多节约20%,九月份比八月份多
节约25%,问该厂食堂九月份节约煤多少公斤?依题意得:x+ (1+20%)x +(1+20%)(1+25%)x=7400
解之,得 答:该食堂九月份节约煤3000公斤.(间接设元)
解:设七月份节约煤x公斤。
则八月份节约煤(1+20%)x 公斤,
九月份节约煤(1+20%)(1+25%)x公斤x=2000(1+20%) (1+25%)x=3000增长率应用题练习1 学校准备添置一批课桌椅,原订购60套,每套 100元。店方表示:如果多购可以优惠,结果
校方购了72套,每套减价3元,但商店获得同样
多的利润,求每套课桌椅的成本是多少?(直接设元)
解:设每套课桌椅的成本价为x 元。
依题意得: 60(100 - x)= 72(100 – 3 – x)
解之,得 x = 82答:每套课桌椅的成本是82元。等量关系:60套时总利润=72套时总利润练习2、某商店经销一种商品,由于进货价降低了5%,售出价 不变,使得利润率有原来的m%提高到(m + 6)%, 求m的值。分析: 等量关系是售出价不变,两种不同利润率下的售价各如何表示?成本我们可以设为“1”
解: (1 + m%)=(1 – 5%)[ 1 +(m + 6)% ]解之,得 m = 14练习3:小颖的父母存三年期教育储蓄,三年后取出了5000元钱,你能求出本金是多少吗?有理数应用题举例 例2 你喜欢吃拉面吗?拉面馆的师傅,用一根很粗的面条,
把两头捏合在一起拉伸,再捏合,再拉伸,反复几次,就
把这根很粗的面条拉成了许多细的面条,如下图所示:
第一次捏合 第二次捏合 第三次捏合(1)这样捏合4次后可拉出多少根面条?5次呢?n次呢?
(2)捏合多少次后可拉出64根面条?3 6 9 12这时s又分别是多少呢? 黑蚂蚁和红蚂蚁都认为自己跑得比对方快,刚好它们看到地上的几个半圆(图1),于是它们决定比一比。黑蚂蚁沿着大半圆从甲处跑到乙处;红蚂蚁沿着两个小半圆也从甲处跑到乙处。两只蚂蚁同时起跑,
(1)?? 两只蚂蚁请你帮助判断:谁跑得快?
?(2)两只蚂蚁对你的判断结果很不满意,决定再到(图2)的几个半圆处再比赛一次,请你猜一猜,哪一只蚂蚁先从甲处跑到乙处?
?
思考
