三角形的边
图片预览






文档简介
课件24张PPT。 7.1.1三角形的边 1、认识三角形,了解三角形的定义,认识三角形的 边、内角、顶点,能用符号语言表示三角形。
2、能从不同角度对三角形进行分类。
3、会运用三角形的三边关系,判断三条线段能否构 成一个三角形。1、在具体图形中不重复地识别所有三角形,并用符 号语言表示。
2、用三角形的三边关系判定三条线段可否组成三角形。学习目标学习重点、难点下面请大家仔细观察一组图片,看看它们有什么共同特点下面请大家仔细观察一组图片,看看它们有什么共同特点
什么样的图形叫三角形?
什么是三角形的边、顶点、内角?
如何用符号语言表示一个三角形?
怎样对三角形进行分类?
通过自学课本63页内容,回答以下问题:一、自主学习 由不在同一条直线上的三条线段首尾顺次相接所组成的图形,叫做三角形。
注意点:
(1)三条线段(2)不在同一直线上
(3)首尾顺次相接(一)三角形的定义 ACB1.线段AB、BC、CA2.点A、B、C3.∠ A、 ∠ B、 ∠ Cabc叫做三角形的边叫做三角形的顶点 叫做三角形的内角,简称三角形的角。
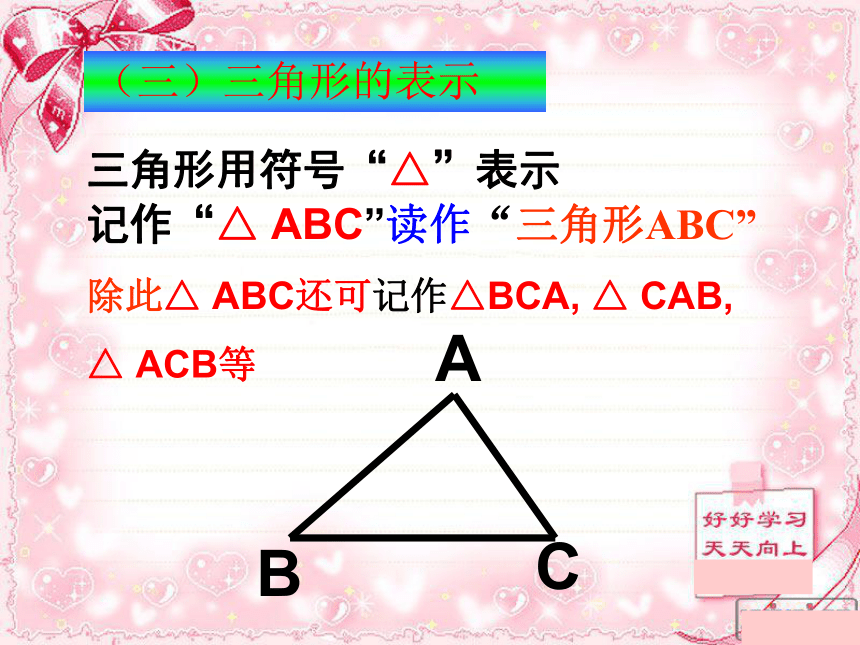
(二)三角形的边、顶点、内角 三角形用符号“△”表示记作“△ ABC”读作“三角形ABC”
除此△ ABC还可记作△BCA, △ CAB,
△ ACB等
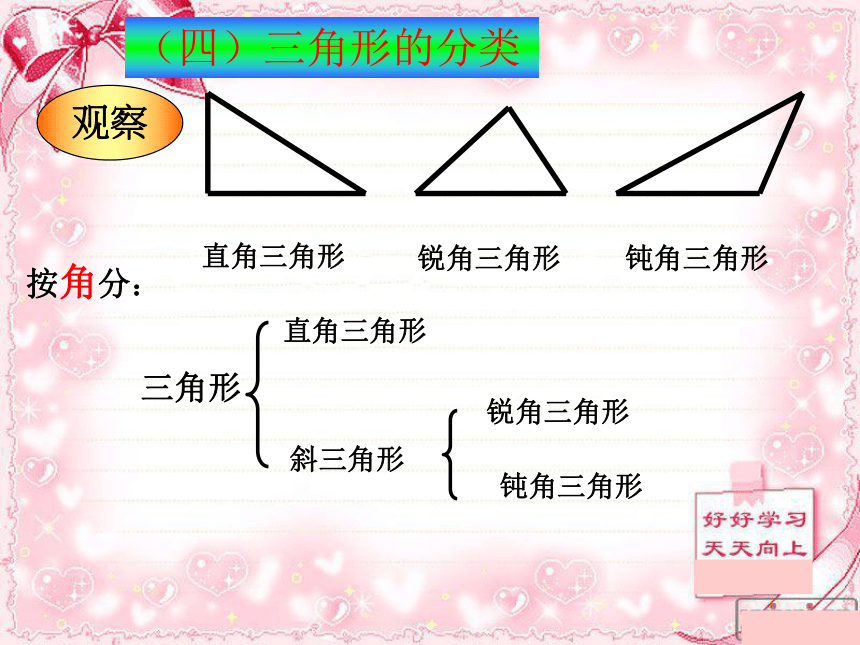
(三)三角形的表示 观察按角分:直角三角形锐角三角形钝角三角形(四)三角形的分类三角形直角三角形锐角三角形钝角三角形斜三角形 再观察等边三角形等腰三角形不等边三角形(四)三角形的分类腰腰底顶角底角底角 底边和腰不相等的等腰三角形按边的相等关系分:三角形不等边三角形等腰三角形等边三角形再观察等边三角形等腰三角形不等边三角形(四)三角形的分类 1.图中共有几个三角形?
用符号表示这些三角形。5个△ABE, △ABC,
△BCE, △BCD ,
△CDE小结:数三角形的个数时,抓住不在同一条
直线上的三个点能组成一个三角形;
再按字母的顺序去数.巩固练习一思考:
怎样数能不重不漏 2.以AB为边的三角形有哪些?△ABC、△ABE3.以点E为顶点的三角形有哪些?△ ABE 、△BCE、 △CDE4.以∠D为角的三角形有哪些?△ BCD、 △DEC巩固练习一 请小组同学们任意画一个△ABC,分别量出AB、 BC 、 AC 的长,并比较下列各式的大小?二、动手操作
AB + BC __ AC;AB + AC __ BC;
AC + BC __ AB,>>>从中你有何启发?小组合作后,对你们的结论加以解释。 如图在△ABC中,
AB + BC__AC
AB + AC__BC;
AC + BC__AB,三角形两边的和大于第三边>>>三角形的三边关系:
三角形三边的关系是判定三条线段能否构成一个三角形的依据.下列长度的三条线段能否组成三角形?为什么?(1) 3,4,8 ( )
(2) 2,5,6 ( )
(3) 5,10,6 ( )
(4) 8,5,3 ( )不能能能不能 只要选取两条较短的线段,求出和再与最长的线段比较 ,和较大则可以组成三角形;否则不能组成三角形。巩固练习二 方法小结: 在A点的小狗,为了尽快吃到B点的香肠,它选择A B路线,而不选择A C B路线,你能用数学知识解释吗?CBA学以致用 理由:三角形两边的和大于第三边或两点之间的所有连线中,线段最短。 例 用一条长18cm的细绳围成一个等腰三角形.
(1)如果腰是底边的2倍,那么各边的长是多少?
(2)能围成一边的长是4cm的等腰三角形吗?
为什么?解:(1)设底边为xcm,则腰长为2xcm
x+2x+2x=18,
解得x=3.6.
所以,三边分别为3.6cm,7.2cm,7.2cm.
三、应用新知 例 用一条长18cm的细绳围成一个等腰三角形.
(1)如果腰是底边的2倍,那么各边的长是多少?
(2)能围成一边的长是4cm的等腰三角形吗?
为什么? (2)因为长4cm的边可能是腰,也可能是底边,所以需要分情况讨论.
如果4cm长的边为底边,设腰长为xcm.则
4+2x=18
解得 x=7
如果4cm长的边为腰,设边长为xcm,则
2×4+x=18
解得x=10
因为4+4<10,出现两边的和小于第三边的
情况,所以不能围成腰长是4cm的等腰三角形.
由以上讨论可知,可以围成底边是4cm的等腰三角形.
三、应用新知 1.现有5cm,6cm,11cm,12cm长的四根木棍,任意选取三根组成一个三角形,那么可以组成三角形的个数为( ) (A)1个(B)2个(C)3个(D)4个B巩固练习三22 总结与反思1、通过这节课的学习活动你有
哪些收获?
2、你还有什么想法吗?
作业必做题:课本P69习题7.1第1、2题
选做题:同步学习P95能力提升
谢谢指导 草原上的四口油井,位于如图所示的A、B、C、D四个位置,现在要建立一个维修站H,问H建在何处,才能使它到四个油井的距离之和HA+HB+HC+HD为最小?说明理由。ADCBHH′1.你认为这个H应该在什么位置?大胆设想!2.到A、C距离和最小的点在哪儿?到B、D?看谁最聪明!
2、能从不同角度对三角形进行分类。
3、会运用三角形的三边关系,判断三条线段能否构 成一个三角形。1、在具体图形中不重复地识别所有三角形,并用符 号语言表示。
2、用三角形的三边关系判定三条线段可否组成三角形。学习目标学习重点、难点下面请大家仔细观察一组图片,看看它们有什么共同特点下面请大家仔细观察一组图片,看看它们有什么共同特点
什么样的图形叫三角形?
什么是三角形的边、顶点、内角?
如何用符号语言表示一个三角形?
怎样对三角形进行分类?
通过自学课本63页内容,回答以下问题:一、自主学习 由不在同一条直线上的三条线段首尾顺次相接所组成的图形,叫做三角形。
注意点:
(1)三条线段(2)不在同一直线上
(3)首尾顺次相接(一)三角形的定义 ACB1.线段AB、BC、CA2.点A、B、C3.∠ A、 ∠ B、 ∠ Cabc叫做三角形的边叫做三角形的顶点 叫做三角形的内角,简称三角形的角。
(二)三角形的边、顶点、内角 三角形用符号“△”表示记作“△ ABC”读作“三角形ABC”
除此△ ABC还可记作△BCA, △ CAB,
△ ACB等
(三)三角形的表示 观察按角分:直角三角形锐角三角形钝角三角形(四)三角形的分类三角形直角三角形锐角三角形钝角三角形斜三角形 再观察等边三角形等腰三角形不等边三角形(四)三角形的分类腰腰底顶角底角底角 底边和腰不相等的等腰三角形按边的相等关系分:三角形不等边三角形等腰三角形等边三角形再观察等边三角形等腰三角形不等边三角形(四)三角形的分类 1.图中共有几个三角形?
用符号表示这些三角形。5个△ABE, △ABC,
△BCE, △BCD ,
△CDE小结:数三角形的个数时,抓住不在同一条
直线上的三个点能组成一个三角形;
再按字母的顺序去数.巩固练习一思考:
怎样数能不重不漏 2.以AB为边的三角形有哪些?△ABC、△ABE3.以点E为顶点的三角形有哪些?△ ABE 、△BCE、 △CDE4.以∠D为角的三角形有哪些?△ BCD、 △DEC巩固练习一 请小组同学们任意画一个△ABC,分别量出AB、 BC 、 AC 的长,并比较下列各式的大小?二、动手操作
AB + BC __ AC;AB + AC __ BC;
AC + BC __ AB,>>>从中你有何启发?小组合作后,对你们的结论加以解释。 如图在△ABC中,
AB + BC__AC
AB + AC__BC;
AC + BC__AB,三角形两边的和大于第三边>>>三角形的三边关系:
三角形三边的关系是判定三条线段能否构成一个三角形的依据.下列长度的三条线段能否组成三角形?为什么?(1) 3,4,8 ( )
(2) 2,5,6 ( )
(3) 5,10,6 ( )
(4) 8,5,3 ( )不能能能不能 只要选取两条较短的线段,求出和再与最长的线段比较 ,和较大则可以组成三角形;否则不能组成三角形。巩固练习二 方法小结: 在A点的小狗,为了尽快吃到B点的香肠,它选择A B路线,而不选择A C B路线,你能用数学知识解释吗?CBA学以致用 理由:三角形两边的和大于第三边或两点之间的所有连线中,线段最短。 例 用一条长18cm的细绳围成一个等腰三角形.
(1)如果腰是底边的2倍,那么各边的长是多少?
(2)能围成一边的长是4cm的等腰三角形吗?
为什么?解:(1)设底边为xcm,则腰长为2xcm
x+2x+2x=18,
解得x=3.6.
所以,三边分别为3.6cm,7.2cm,7.2cm.
三、应用新知 例 用一条长18cm的细绳围成一个等腰三角形.
(1)如果腰是底边的2倍,那么各边的长是多少?
(2)能围成一边的长是4cm的等腰三角形吗?
为什么? (2)因为长4cm的边可能是腰,也可能是底边,所以需要分情况讨论.
如果4cm长的边为底边,设腰长为xcm.则
4+2x=18
解得 x=7
如果4cm长的边为腰,设边长为xcm,则
2×4+x=18
解得x=10
因为4+4<10,出现两边的和小于第三边的
情况,所以不能围成腰长是4cm的等腰三角形.
由以上讨论可知,可以围成底边是4cm的等腰三角形.
三、应用新知 1.现有5cm,6cm,11cm,12cm长的四根木棍,任意选取三根组成一个三角形,那么可以组成三角形的个数为( ) (A)1个(B)2个(C)3个(D)4个B巩固练习三22 总结与反思1、通过这节课的学习活动你有
哪些收获?
2、你还有什么想法吗?
作业必做题:课本P69习题7.1第1、2题
选做题:同步学习P95能力提升
谢谢指导 草原上的四口油井,位于如图所示的A、B、C、D四个位置,现在要建立一个维修站H,问H建在何处,才能使它到四个油井的距离之和HA+HB+HC+HD为最小?说明理由。ADCBHH′1.你认为这个H应该在什么位置?大胆设想!2.到A、C距离和最小的点在哪儿?到B、D?看谁最聪明!
