24.1.3 弧、弦、圆心角
文档属性
| 名称 | 24.1.3 弧、弦、圆心角 |

|
|
| 格式 | rar | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-24 00:00:00 | ||
图片预览





文档简介
课件22张PPT。义务教育课程标准实验教科书九年级 上册人民教育出版社24.1.3 弧、弦、圆心角圆的对称性及特性圆是轴对称图形,圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.驶向胜利的彼岸圆也是中心对称图形,它的对称中心就是圆心.用旋转的方法可以得到:一个圆绕着它的圆心旋转任意一个角度,都能与原来的图形重合.这是圆特有的一个性质:圆的旋转不变性 过点O作弦AB的垂线, 垂足
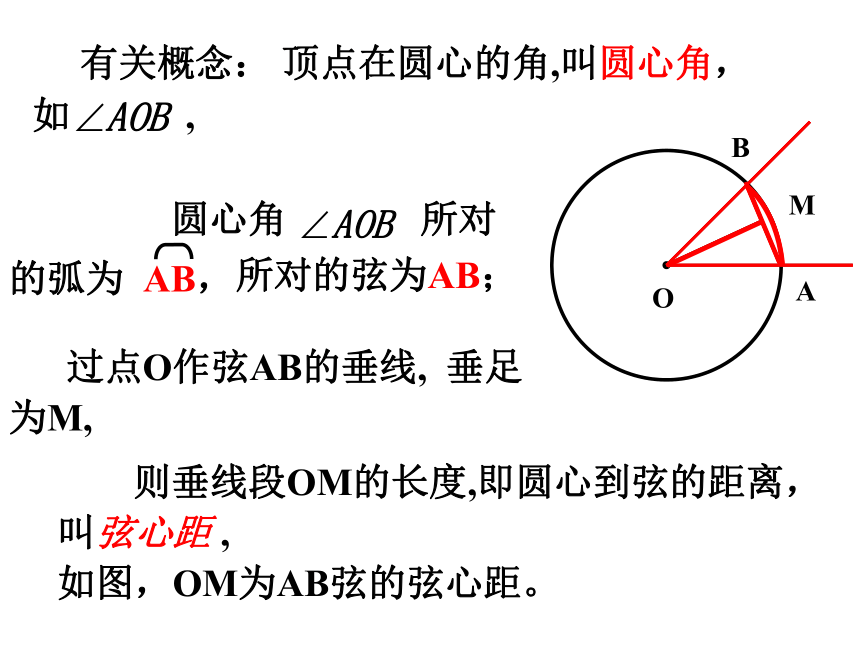
为M,AB 有关概念: 顶点在圆心的角,叫圆心角,
如 , 所对的弦为AB; 则垂线段OM的长度,即圆心到弦的距离,叫弦心距 ,
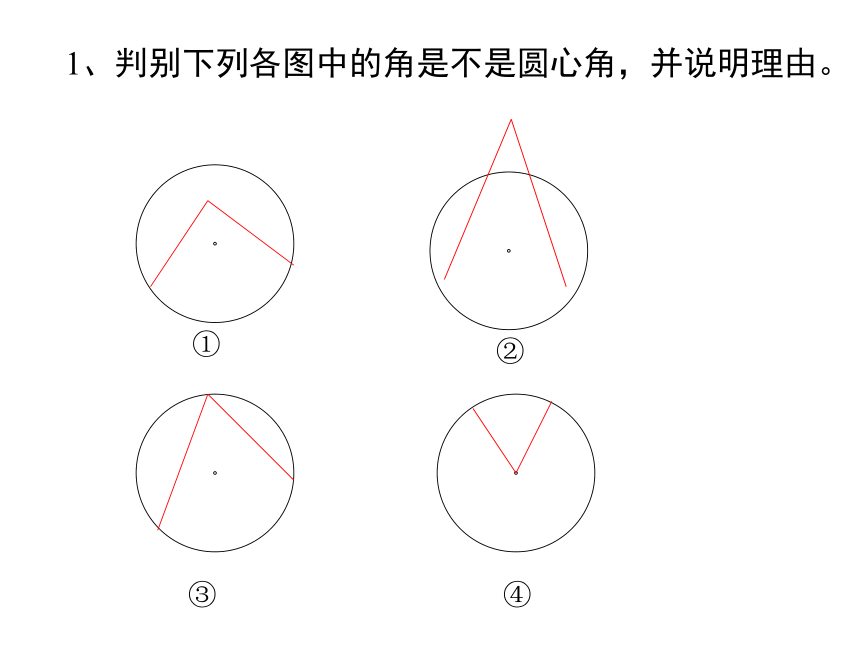
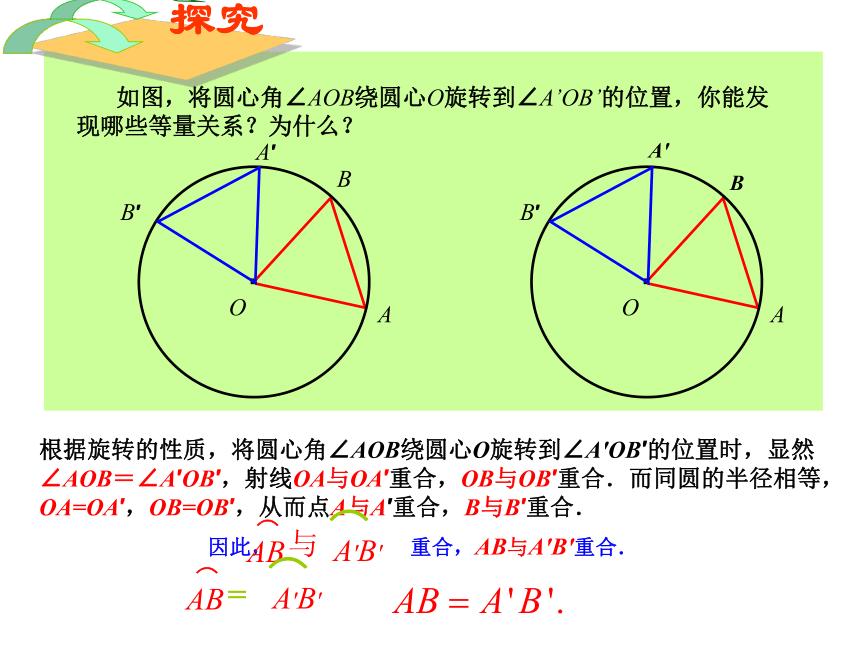
如图,OM为AB弦的弦心距。1、判别下列各图中的角是不是圆心角,并说明理由。①②③④2、下列图中弦心距做对了的是( )┐┐①②③④任意给圆心角,对应出现四个量:圆心角弧弦 弦心距 如图,将圆心角∠AOB绕圆心O旋转到∠A’OB’的位置,你能发现哪些等量关系?为什么?根据旋转的性质,将圆心角∠AOB绕圆心O旋转到∠A′OB′的位置时,显然∠AOB=∠A′OB′,射线OA与OA′重合,OB与OB′重合.而同圆的半径相等,OA=OA′,OB=OB′,从而点A与A′重合,B与B′重合.·OAB·OABA′B′A′B′因此, 重合,AB与A′B′重合.这样,我们就得到下面的定理:弧、弦与圆心角的关系定理定理(等对等定理)在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等吗?由条件:
①∠AOB=∠A′O′B′③AB=A′B′④ OD=O′D′在同圆或等圆中,如果轮换下面四组条件:
①两个圆心角,②两条弧,③两条弦,④两条弦心距,你能得出什么结论?与同伴交流你的想法和理由.如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′推论在同圆或等圆中,如果①两个圆心角,
②两条弧,③两条弦,④两条弦心距中,
有一组量相等,那么它们所对应的
其余各组量都分别相等.如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′相等相等相等结论:相等以上四句话如没有在同圆或等圆中,这个结论还会成立吗?相等相等相等相等相等练习1、已知:如图,AB、CD是⊙O的两条弦,OE、OF为AB、CD的弦心距,根据本节定理及推论填空:
(1)如果AB=CD,那么
_____________,________,____________。
(2)如果OE=OF,那么
_____________,________,__________。
(3)如果AB=CD 那么
______________,__________,_________。
(4)如果∠AOB=∠COD,那么
_________,________,_________ 。⌒
⌒
∠AOB=∠COD AB=CD OE=OF 如图,在⊙O中, , ∠ACB=60o 求 证: ∠AOB= ∠BOC = ∠AOC。
证明: ∵
∴ AB=AC △ABC是等腰三角形
又∠ACB=60o
∴ △ABC是等边三角形,AB=BC=CA
∴ ∠AOB= ∠BOC = ∠AOCACOB例 如图,已知点O是∠EPF 的平分线上一点,P点在圆外,
以O为圆心的圆与∠EPF 的两边分别相交于A、B和C、D。
求证:AB=CD分析: 联想到“角平分线的性质”,作弦心距OM、ON, 证明: 作 , 垂足分别为M 、 N 。.PABECDF要证AB=CD ,只需证OM=ONO.如图,P点在圆上,PB=PD吗?
P点在圆内,AB=CD吗?思考:PBEDFO一.判断下列说法是否正确:
1、相等的圆心角所对的弧相等。( )
2、相等的弧所对的弦相等。( )
二.如图,⊙O中,AB=CD,
,则试一试你的能力 你会做吗?解:∵(已知)∴∴∴∠1=∠2=45°(在同圆中,相等的弧所对的圆心角相等)小结:
在同圆或等圆中,如果①两个圆心角,
②两条弧,③两条弦,④两条弦心距中,
有一组量相等,那么它们所对应的
其余各组量都分别相等.
如图7所示,CD为⊙O的弦,在CD上取CE=DF,连结OE、OF,并延长交⊙O于点A、B。
(1)试判断△OEF的形状,并说明理由;
(2)求证:弧AC=弧BD拓展训练 在⊙O中,
那么弦AB与弦CD的关系为( )
AB=2CD B.AB>2CD
C.AB<2CD D.AB=CD拓展训练 在⊙O中, AB=2CD
那么 的关系为( )
B.
C. D. AB= CDAB与 2CD3、如图,已知AD=BC、求证AB=CD变式:如图,如果弧AD=弧BC,求证:AB=CD
为M,AB 有关概念: 顶点在圆心的角,叫圆心角,
如 , 所对的弦为AB; 则垂线段OM的长度,即圆心到弦的距离,叫弦心距 ,
如图,OM为AB弦的弦心距。1、判别下列各图中的角是不是圆心角,并说明理由。①②③④2、下列图中弦心距做对了的是( )┐┐①②③④任意给圆心角,对应出现四个量:圆心角弧弦 弦心距 如图,将圆心角∠AOB绕圆心O旋转到∠A’OB’的位置,你能发现哪些等量关系?为什么?根据旋转的性质,将圆心角∠AOB绕圆心O旋转到∠A′OB′的位置时,显然∠AOB=∠A′OB′,射线OA与OA′重合,OB与OB′重合.而同圆的半径相等,OA=OA′,OB=OB′,从而点A与A′重合,B与B′重合.·OAB·OABA′B′A′B′因此, 重合,AB与A′B′重合.这样,我们就得到下面的定理:弧、弦与圆心角的关系定理定理(等对等定理)在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等吗?由条件:
①∠AOB=∠A′O′B′③AB=A′B′④ OD=O′D′在同圆或等圆中,如果轮换下面四组条件:
①两个圆心角,②两条弧,③两条弦,④两条弦心距,你能得出什么结论?与同伴交流你的想法和理由.如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′推论在同圆或等圆中,如果①两个圆心角,
②两条弧,③两条弦,④两条弦心距中,
有一组量相等,那么它们所对应的
其余各组量都分别相等.如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′相等相等相等结论:相等以上四句话如没有在同圆或等圆中,这个结论还会成立吗?相等相等相等相等相等练习1、已知:如图,AB、CD是⊙O的两条弦,OE、OF为AB、CD的弦心距,根据本节定理及推论填空:
(1)如果AB=CD,那么
_____________,________,____________。
(2)如果OE=OF,那么
_____________,________,__________。
(3)如果AB=CD 那么
______________,__________,_________。
(4)如果∠AOB=∠COD,那么
_________,________,_________ 。⌒
⌒
∠AOB=∠COD AB=CD OE=OF 如图,在⊙O中, , ∠ACB=60o 求 证: ∠AOB= ∠BOC = ∠AOC。
证明: ∵
∴ AB=AC △ABC是等腰三角形
又∠ACB=60o
∴ △ABC是等边三角形,AB=BC=CA
∴ ∠AOB= ∠BOC = ∠AOCACOB例 如图,已知点O是∠EPF 的平分线上一点,P点在圆外,
以O为圆心的圆与∠EPF 的两边分别相交于A、B和C、D。
求证:AB=CD分析: 联想到“角平分线的性质”,作弦心距OM、ON, 证明: 作 , 垂足分别为M 、 N 。.PABECDF要证AB=CD ,只需证OM=ONO.如图,P点在圆上,PB=PD吗?
P点在圆内,AB=CD吗?思考:PBEDFO一.判断下列说法是否正确:
1、相等的圆心角所对的弧相等。( )
2、相等的弧所对的弦相等。( )
二.如图,⊙O中,AB=CD,
,则试一试你的能力 你会做吗?解:∵(已知)∴∴∴∠1=∠2=45°(在同圆中,相等的弧所对的圆心角相等)小结:
在同圆或等圆中,如果①两个圆心角,
②两条弧,③两条弦,④两条弦心距中,
有一组量相等,那么它们所对应的
其余各组量都分别相等.
如图7所示,CD为⊙O的弦,在CD上取CE=DF,连结OE、OF,并延长交⊙O于点A、B。
(1)试判断△OEF的形状,并说明理由;
(2)求证:弧AC=弧BD拓展训练 在⊙O中,
那么弦AB与弦CD的关系为( )
AB=2CD B.AB>2CD
C.AB<2CD D.AB=CD拓展训练 在⊙O中, AB=2CD
那么 的关系为( )
B.
C. D. AB= CDAB与 2CD3、如图,已知AD=BC、求证AB=CD变式:如图,如果弧AD=弧BC,求证:AB=CD
同课章节目录
