24.1.4圆周角 2

课件13张PPT。24.1.4圆周角(2)特征：① 角的顶点在圆上.② 角的两边都与圆相交.1、圆周角定义: 顶点在圆上,
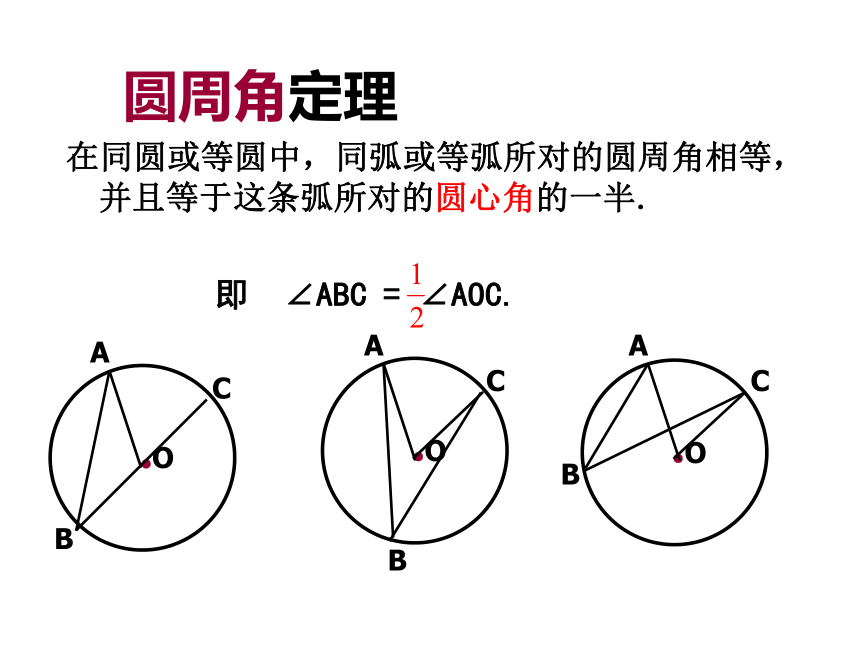
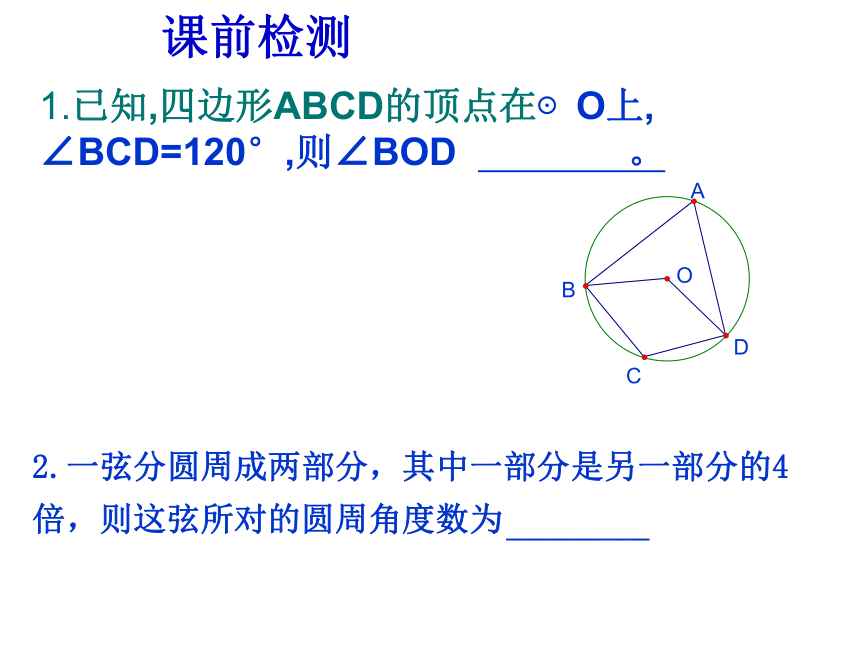
并且两边都和圆相交的角叫圆周角.一、旧知回放:圆周角定理在同圆或等圆中，同弧或等弧所对的圆周角相等，并且等于这条弧所对的圆心角的一半.即 ∠ABC = ∠AOC.问题解答1、圆周角定理的推论1：2、圆周角定理的推论2：半圆或直径所对的圆周角都相等,都等于90°(直角).反过来也是成立的,即90°的圆周角所对的弦是圆的直径在同圆或等圆中，如果两个圆周角相等，那么它们所对的弧一定相等课前检测1.已知,四边形ABCD的顶点在⊙O上, ∠BCD=120°,则∠BOD 。证明：已知:如图,四边形ABCD的四个顶点在⊙O上，求证：∠B+∠D=1800ＯＣＢＡＤ例1: 船在航行过程中，船长常常通过测定角度来确定是否会遇到暗礁。如图A,B表示灯塔，暗礁分布在经过A,B两点的一个圆形区域内，C表示一个危险临界点，∠ACB就是“危险角”，当船与两个灯塔的夹角大于“危险角”时，就有可能触礁。弓形所含的圆周角∠C=50°,问船在航行时怎样才能保证不进入暗礁区?（1）当船与两个灯塔的夹角∠α大于“危险角”时，船位于哪个区域？为什么？（2）当船与两个灯塔的夹角∠α小于“危险角”时，船位于哪个区域？为什么？例题 例 2:如图,已知A、B、C、D、E 均在⊙O上，且AC为⊙O的直径，求
∠A+ ∠B+ ∠C的值。例 3 : 如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到C,使AC=AB,BD与CD有什么关系.为什么?变:若AC交⊙O于点E,
求证:CD=DE=BD1、100o的弧所对的圆心角等于_______，所对的圆周角等于_______。
2、一弦分圆周角成两部分，其中一部分是另一部分的4倍，则这弦所对的圆周角度数为________________。
3、如图，在⊙O中，∠BAC=32o，则∠BOC=________。
4、如图，⊙O中，∠ACB = 130o，则∠AOB=______。
5、下列命题中是真命题的是（ ）
（A）顶点在圆周上的角叫做圆周角。
（B）60o的圆周角所对的弧的度数是30o
（C）一弧所对的圆周角等于它所对的圆心角。
（D）120o的弧所对的圆周角是60oB
100o50o36o或144o64o100oD练习6,如图所示，AB，AC是⊙O的弦，AD⊥BC于D，交⊙O于F，AE与⊙O的直径，试问两弦BE与CF的大小有何关系，说明理由．