切线复习

课件13张PPT。圆的切线（复习课）切线的判定定理：
切线的性质定理：
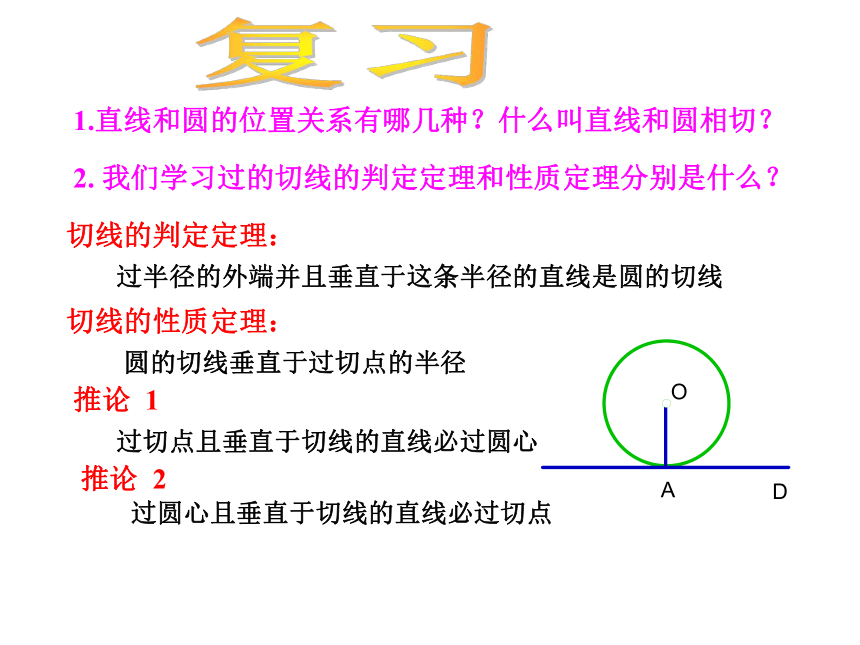
复习2. 我们学习过的切线的判定定理和性质定理分别是什么？过半径的外端并且垂直于这条半径的直线是圆的切线圆的切线垂直于过切点的半径
推论 1推论 2 过切点且垂直于切线的直线必过圆心过圆心且垂直于切线的直线必过切点1.直线和圆的位置关系有哪几种？什么叫直线和圆相切？
(1) 当已知条件中没有明确给出直线与圆有公共点时,常过圆心作该直线的垂线段,证明该垂线段的长等于半径,也就是“ ”。切线的判定方法 (2)当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线，也就是“ ”。作垂直,证半径连半径,证垂直 根据切线的性质 , 遇到切点 , 连接半径 , 这是在圆中添加辅助线的常用方法之一 方法技巧切线的性质判断对错（1）和圆有公共点的直线是圆的切线。 （ ）
（2）经过半径的一个端点并且垂直于这条半径的直线是
圆的切线。 （ ）
（3）若一条直线与圆的直径垂直，则这条直线就是圆
的切线。
（4）到圆心的距离等于半径的直线是圆的切线 。 （ ）
（5）与两条平行线都相切的圆的直径等于这两条平行线
间的距离。 （ ）
（6）与等边三角形的两边相切的圆必定与第三边相切。
( )
（7）过切点的直径垂直于切线。 ( )× × × × 小红家的锅盖坏了,为了配一个锅盖,需要测量锅盖的
直径(锅边所形成的圆的直径),而小红家只有一把长20cm
的直尺,根本不够长,怎么办呢?小红想了想,采取以下方
法:首先把锅平放到墙根,锅边刚好靠到两墙,用直尺紧贴
墙面量得MA的长,即可求出墙的直径,请你利用下图,说
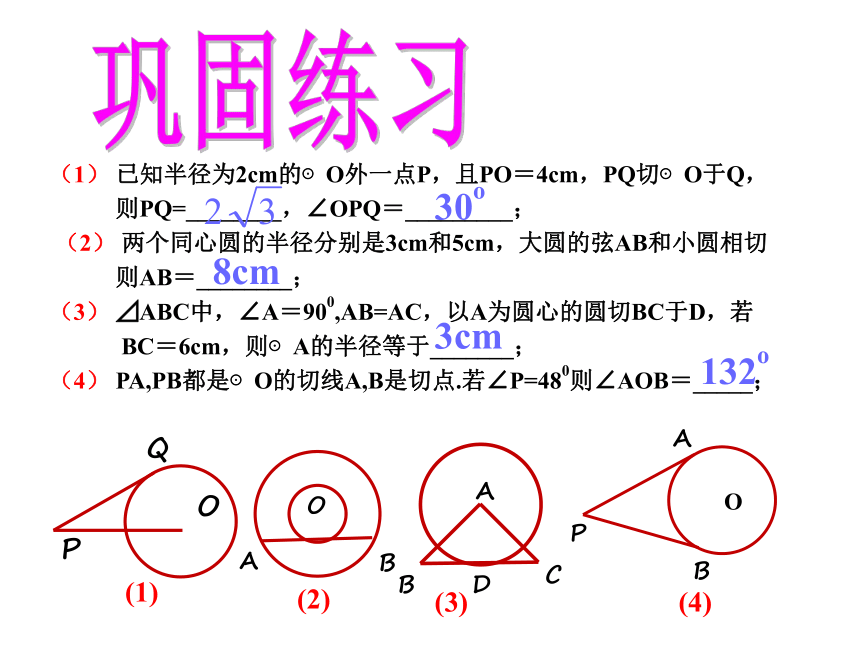
明她这样做的道理.例 ：巩固练习（1） 已知半径为2cm的⊙O外一点P，且PO＝4cm，PQ切⊙O于Q，
则PQ=________，∠OPQ＝_________；
?（2） 两个同心圆的半径分别是3cm和5cm，大圆的弦AB和小圆相切
则AB＝________；
（3） ⊿ABC中，∠A＝900,AB=AC，以A为圆心的圆切BC于D，若
BC＝6cm，则⊙A的半径等于_______；
（4） PA,PB都是⊙O的切线A,B是切点.若∠P=480则∠AOB＝_____；
30o8cm3cm132o(6) 已知： 如图,⊙O交OA于C,弦BC＝AC,∠A＝300
求证： AB是⊙C的切线
?? (7) 如图,⊿ABC中,∠C＝900,AC=12cm,BC=6cm 点O在
AB上, ⊙O分别切AC,BC于E,F.
求 ⊙O的半径
(5) 已知: 如图,在以O为圆心的两个同心圆中,大圆的弦AB
和CD 相等,且AB与小圆相切于E
求证：CD与小圆相切
1、若AB是⊙O的直径，点C在⊙O上，过C引直径AB的垂线，垂足是D，点D分这条直径成2︰3两部分，如果⊙O的半径等于5，则BC=_____________。 2、已知⊙O的弦CD 直径AB，垂足为P，且AP=3，AB=30，那么CD等于 (　　 ) A. 9　　 B. 　　 C.18　　 D. 3、PT切⊙O于T，PAB为经过圆心O的割线，交⊙O于A，B两点，若PT=4，PA=2，则 ⊙O的半径为： （ ）6、已知：AB是圆O的直径，C是AB延长线上的一点，CD切圆O于点D，DE⊥AB于点E。
求证： ∠CDB = ∠EDB已知,如图,D(0,1),⊙D交y轴于A、B两点,交x负半
轴于C点,过C点的直线:y=－2x－4与y轴交于P.
⑴试猜想PC与⊙D的位置关系，并说明理由.分析：做此类题，尤其强调
数形结合，同学们应把题中
数据“放入”图中。猜想直线
PC与⊙D相切。怎么证？联
想证明切线的两种方法。点
C在圆上，即证：∠DCP=90°
利用勾股及逆定理可得。切
线
判
定令x=0，得y=-4;令y=0,得x=-2
∴C(-2,0), P(0,-4)
又∵D(0,1) ∴OC=2, OP=4 ,OD=1, DP=5又∵在Rt△COD中, CD2=OC2+OD2=4+1=5
在Rt△COP中, CP2=OC2+OP2=4+16=20在△CPD中, CD2+CP2=5+20=25, DP2=25∴CD2+CP2=DP2即：△CDP为直角三角形,且∠DCP=90°
∴PC为⊙D的切线.证明：∵直线y=-2x-4解： PC是⊙O的切线，勾股（逆）定理知识升华圆与一次函数已知,如图,D(0,1),⊙D交y轴于A、B两点,交x轴负
半轴于C点,过C点的直线:y=－2x－4与y轴交于P.
⑵判断在直线PC上是否存在点E，使得S△EOC=
4S△CDO,若存在，求出点E的坐标；若不存在，
请说明理由.
存
在
性
问
题知识升华圆与一次函数解：假设在直线PC上存在这样的点E(x0,y0),使得S△EOC =4S △CDO，∵E点在直线PC：y=-2x-4上，∴当y0=4时有： 当y0=-4时有：∴在直线PC上存在满足条件的E点，其的坐标为(-4,4) , (0,-4) .抓住不变量
分类讨论课堂小节
2. 根据切线的性质,构造相似三角形,利用相似三角形对
应边成比例的性质,建立方程求解,是圆的计算中常用
的一种方法。(如例3）