切线长定理 1

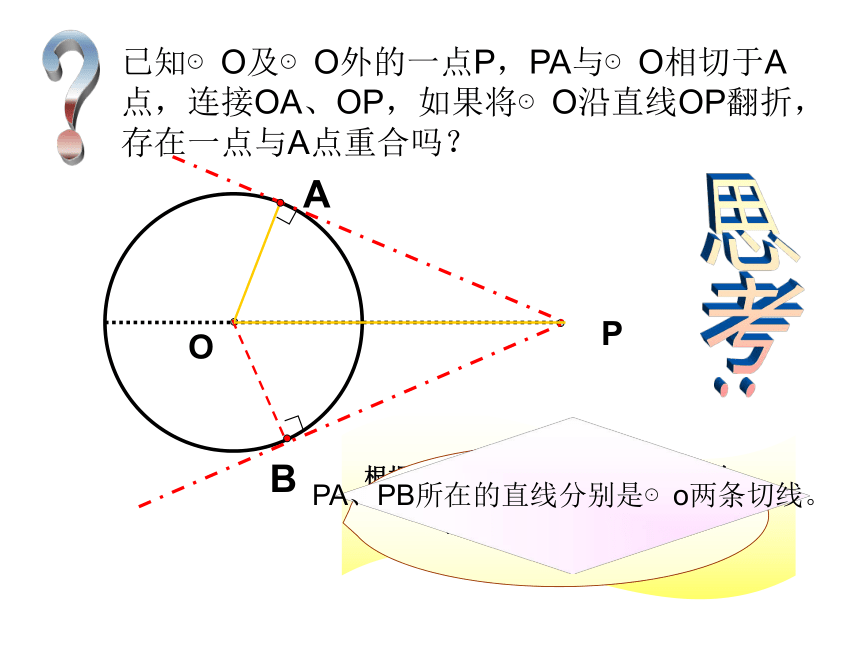
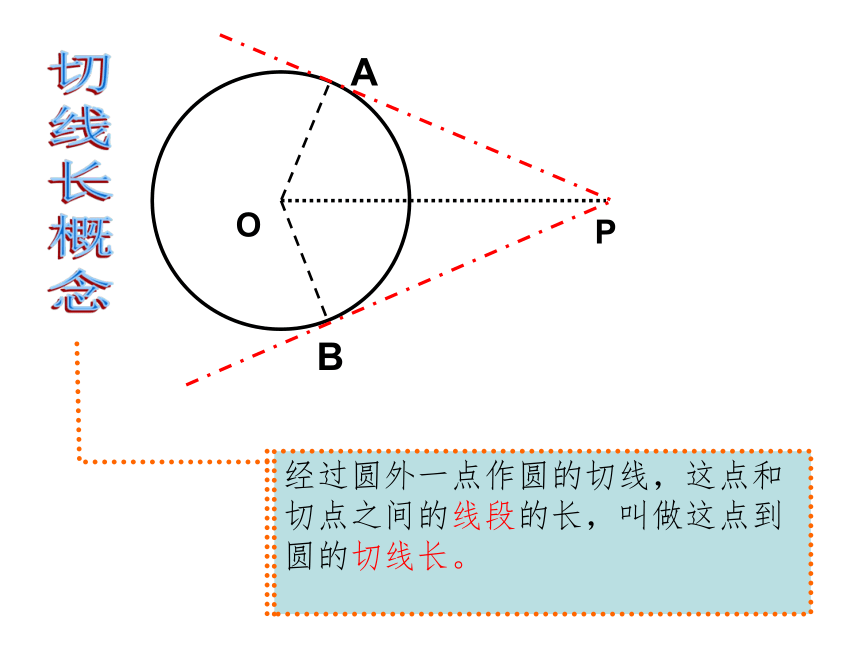
课件23张PPT。切线长定理已知⊙O及⊙O外的一点P，PA与⊙O相切于A点，连接OA、OP，如果将⊙O沿直线OP翻折，存在一点与A点重合吗？思考:？OPAB你能发现OA与PA，OB与PB之间的关系吗？PA、PB所在的直线分别是⊙o两条切线。∟∟切线长概念经过圆外一点作圆的切线，这点和切点之间的线段的长，叫做这点到圆的切线长。OPAB
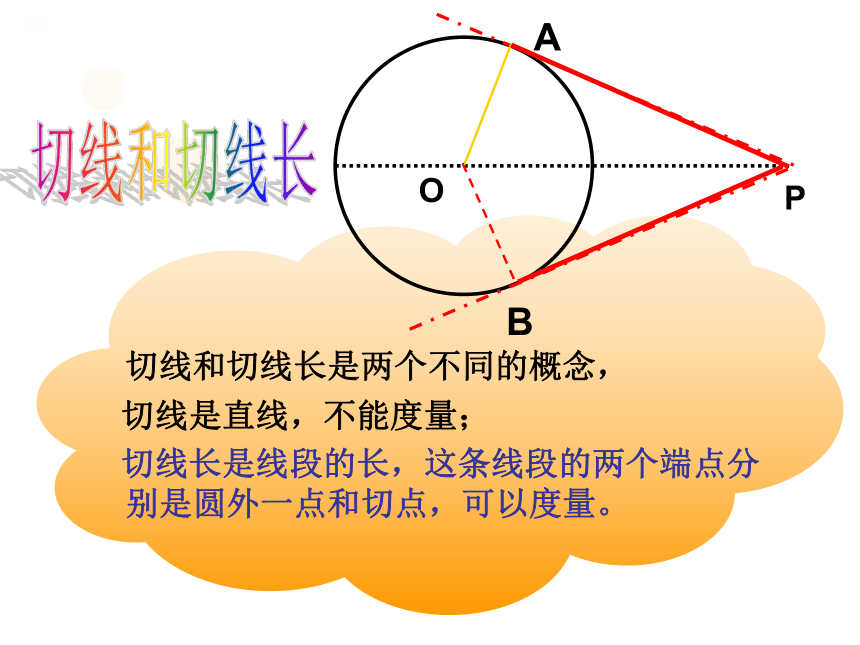
切线和切线长是两个不同的概念，
切线是直线，不能度量；
切线长是线段的长，这条线段的两个端点分别是圆外一点和切点，可以度量。切线和切线长OPAB∟∟M根据你的直观判断，猜想图中PA是否等于PB？∠1与∠2又有什么关系？大胆猜想:
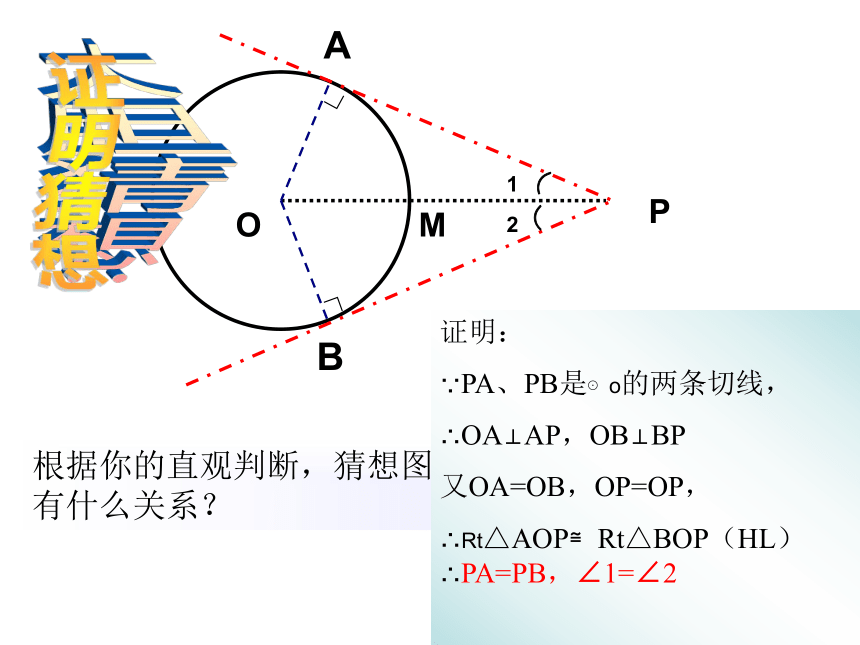
　　⌒⌒12证明：
∵PA、PB是⊙o的两条切线，
∴OA⊥AP，OB⊥BP
又OA=OB，OP=OP，
∴Rt△AOP≌Rt△BOP（HL）∴PA=PB，∠1=∠2
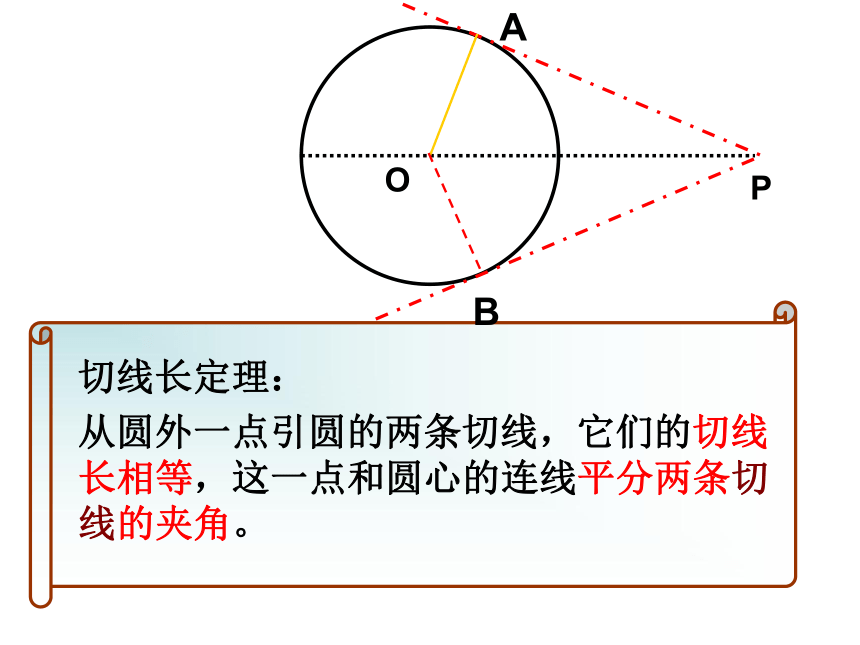
证明猜想 切线长定理：
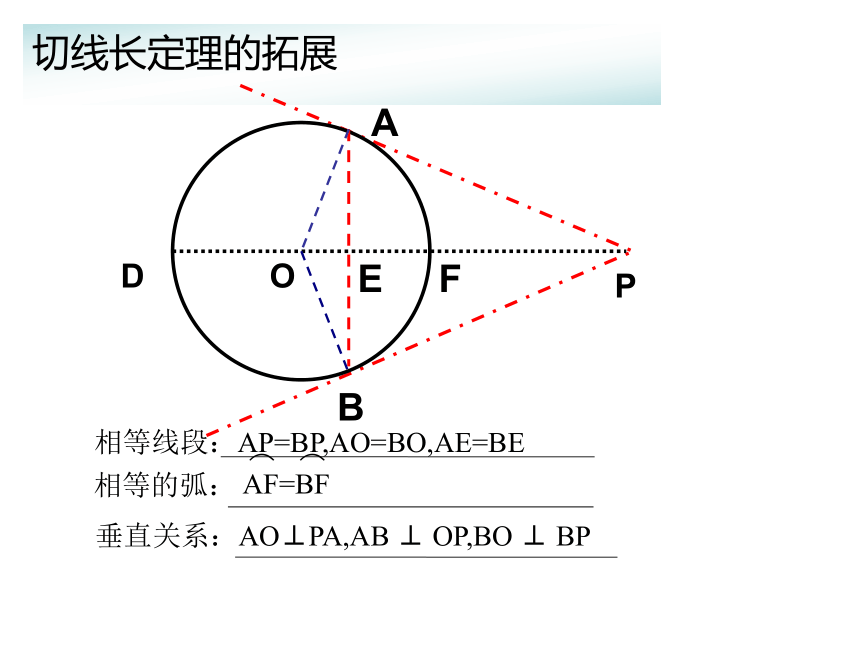
从圆外一点引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角。切线长定理的拓展
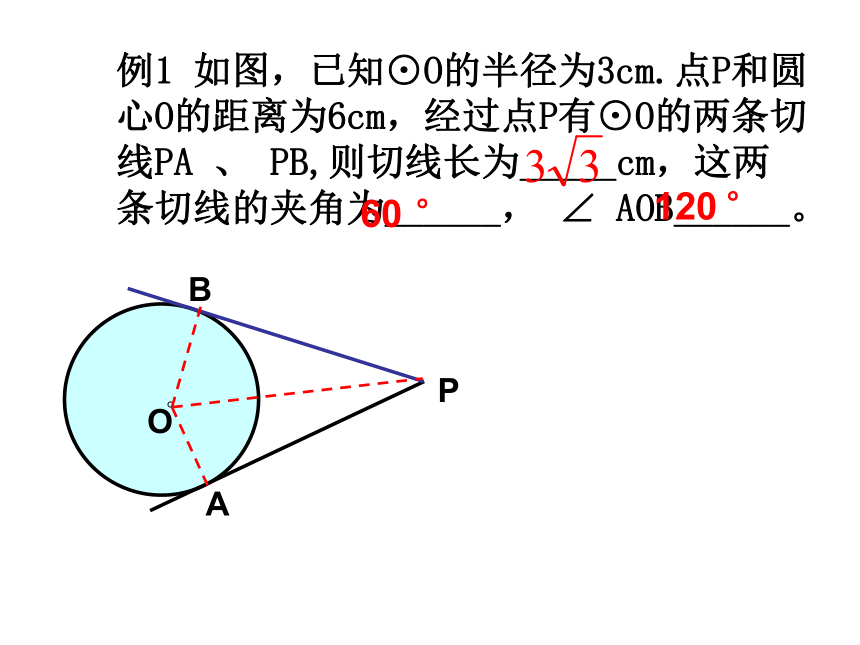
　　BOPAEDF相等线段：AP=BP,AO=BO,AE=BE相等的弧：垂直关系：AO⊥PA,AB ⊥ OP,BO ⊥ BP例1 如图，已知⊙O的半径为3cm.点P和圆心O的距离为6cm，经过点P有⊙O的两条切线PA 、 PB,则切线长为_____cm，这两条切线的夹角为______， ∠ AOB______。60 °120 °形成性练习：
点P和圆心O的距离为6cm ，过P有圆O的两条切线PA、PB。
①若半径为3cm,求切线长、切线夹角∠APB。
②若∠APB=600 ，OP=6cm,求 半径及AP。
③若AB=6cm, ∠APB=600 , 求OP.拓展： 如图，从⊙O外一点P作⊙O的两条切线，分别切⊙O于A 、B，在AB上任取一点C作⊙O的切线分别交PA 、PB于D 、E
（1）若PA=2，则△PDE的周长为____；若PA=a，则△PDE的周长为_____。
（2）连结OD 、OE，若∠P=40 °，则∠DOE=_____;若∠P=k,∠DOE=___________ 度 。E · OCBDPA42a70 °例2. 已知：P为圆O外一点，PA，PB为圆O的切线，A，B为切点，BC是直径。
求证：AC∥OP。PABOC。PBAO反思：在解决有关圆的切线长的问题时，往往需要我们构建基本图形。（3）连结圆心和圆外一点（角平分线）（2）连结两切点（等腰三角形）（1）分别连结圆心和切点（直角）
思 考一张三角形的铁皮，如何在它上面截下一块圆形的用料，并且使圆的面积尽可能大呢？三角形的内切圆：与三角形各边都相切的圆叫做三角形的内切圆三角形的内心：三角形的内切圆的圆心（即三角形三条角平分线的交点）例题：如图， △ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F，且AB=9cm,BC=14cm，CA=13cm，求AF、BD、CE的长。x13﹣xx13﹣x9﹣x9﹣x在边长为3cm，4cm，5cm的三角形
的铁皮上剪下一个最大的圆，
求此圆的半径ABDLMNPO圆的外切四边形的两组对边和相等。已知：四边形ABCD的边 AB，BC，CD，DA和圆O分别相切于L，M，N，P。
探索圆外切四边形边的关系。CBL=BM=wDN=DP=x
AP=AL=y
CN=CM=z
练习．某梯形中位线为18cm,且梯形有内切圆，求梯形周长。练 习 1如图，△ABC中，∠ ABC=50°，∠ACB=75 °，点O
是⊙O的内心，求∠ BOC的度数。AOCB解：∵点O是⊙O的内心
∴∠OBC=1/2∠ABC=25°

∠OCB=1/2∠ACB=37.5°
∴ ∠BOC=180°﹣25°﹣37.5°
=117.5°练 习 2△ABC的内切圆半径为 r , △ABC的周长为 l ,求△ABC
的面积。 （提示：设内心为O，连接OA、OB、OC。）解：连接OA、OB、OC，则
S= AB × r + AC × r + BC × r
= (AB +AC+BC) × r
= l rrrr小结：（1）切线长定理。（2）连接圆心和切点是我们解决切线长定理相关问题时常用的辅助线。巩固性练习：
1．已知：如图，△ABC 中，∠ABC=90 ，AB上一点O，以O为圆心的⊙O交OA于E，切AC于D，AD＝2，AE＝1，求CD的长。3、如图，AB是⊙O的直径，AD、DC、BC是切线，点A、E、B为切点， (1)求证：OD ⊥ OC (2)若BC=9，AD=4，
求OB的长.练一练想一想如图：用两根带有刻度的木条做一个夹角为60°的工具尺，你能用它量出一个圆的半径吗？若量出角的顶点到切点的距离为10cm，试求这个圆半径的近似值。